一道解析几何么,,,
其实就是求直线与圆的切线。
看到方法有很多,比如根据角度之类的。
这里主要用到了初中的几何知识。
考虑这幅图。
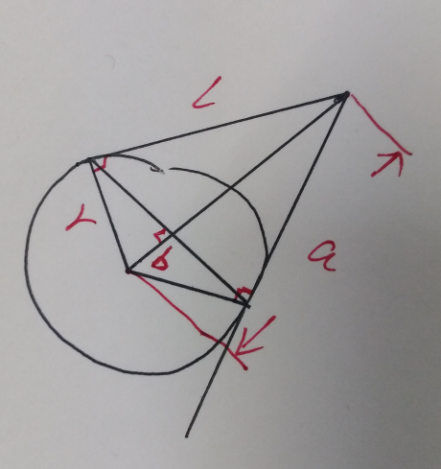
首先可以根据相似三角形知道b的长度,同时圆心与点的方向也知道。 那么 圆心+b 就是 切点连线 与 点与圆心 连线的交点了。
然后根据 面积,有 l·r = (b的长度)*(中间点到切点的长度) .
就很容易得到切点了。详细看代码,poj返回vector好像会RE,就改成pair了。

1 #include <cstdio> 2 #include <cmath> 3 #include <algorithm> 4 #include <vector> 5 #include <map> 6 #include <cstring> 7 using namespace std; 8 typedef double db; 9 const db eps = 1e-7; 10 const db pi = acos(-1); 11 int sign(db k){ 12 if (k>eps) return 1; else if (k<-eps) return -1; return 0; 13 } 14 int cmp(db k1,db k2){return sign(k1-k2);} 15 struct point{ 16 db x,y; 17 point operator + (const point &k1) const{return (point){k1.x+x,k1.y+y};} 18 point operator - (const point &k1) const{return (point){x-k1.x,y-k1.y};} 19 point operator * (db k1) const{return (point){x*k1,y*k1};} 20 point operator / (db k1) const{return (point){x/k1,y/k1};} 21 point turn(db k1){ return (point){x*cos(k1)-y*sin(k1),x*sin(k1)+y*cos(k1)};} 22 point turn90(){ return (point){-y,x};} 23 db abs(){ return sqrt(x*x+y*y);} 24 db abs2(){ return x*x+y*y;} 25 db dis(point k1){ return (*this-k1).abs();} 26 point unit(){db w=abs(); return (point){x/w,y/w};} 27 }; 28 db cross(point k1,point k2){ return k1.x*k2.y-k1.y*k2.x;} 29 db dot(point k1,point k2){ return k1.x*k2.x+k1.y*k2.y;} 30 point proj(point k1,point k2,point q){ 31 point k=k2-k1; 32 return k1+k*(dot(q-k1,k)/k.abs2()); 33 } 34 point getLL(point k1,point k2,point k3,point k4){ 35 db w1=cross(k1-k3,k4-k3),w2=cross(k4-k3,k2-k3); 36 return (k1*w2+k2*w1)/(w1+w2); 37 } 38 struct circle{ 39 point o;db r; 40 int inside(point k){ return cmp(r,o.dis(k));} 41 }; 42 pair<point,point> TangentCP(circle k1,point k2){// 43 db a=(k2-k1.o).abs(),b=k1.r*k1.r/a,c=sqrt(max((db)0.0,k1.r*k1.r-b*b)); 44 point k=(k2-k1.o).unit(),m=k1.o+k*b,del=k.turn90()*c; 45 return {m-del,m+del}; 46 } 47 struct line{ 48 db l,r; 49 }; 50 bool cmp2(line a,line b){ 51 return a.l<b.l; 52 } 53 int n; 54 line l[1551]; 55 circle c[1551]; 56 pair<point,point> g; 57 point e,s1,s2; 58 int main(){ 59 bool f=0; 60 while (scanf("%d",&n)&&n){ 61 if(f)printf(" "); 62 f=1; 63 scanf("%lf%lf",&e.x,&e.y); 64 for(int i=1;i<=n;i++){ 65 scanf("%lf%lf%lf",&c[i].o.x,&c[i].o.y,&c[i].r); 66 } 67 for(int i=1;i<=n;i++){ 68 g=TangentCP(c[i],e); 69 s1 = getLL(e,g.first,point{0.0,0.0},point{100.0,0.0}); 70 s2 = getLL(e,g.second,point{0.0,0.0},point{100.0,0.0}); 71 l[i]=line{s2.x,s1.x}; 72 } 73 sort(l+1,l+1+n,cmp2); 74 db L = l[1].l,R = l[1].r; 75 for(int i=2;i<=n;i++){ 76 if(l[i].l>R){ 77 printf("%.2f %.2f ",L,R); 78 L = l[i].l,R=l[i].r; 79 } else 80 R = max(R,l[i].r); 81 } 82 printf("%.2f %.2f ",L,R); 83 } 84 } 85 /** 86 * 87 1 88 300 300 89 390 150 90 90 0 91 92 6 93 300 450 94 70 50 30 95 120 20 20 96 270 40 10 97 250 85 20 98 220 30 30 99 380 100 100 100 */
