jzoj6384. 【NOIP2019模拟2019.10.23】珂学家

Description

Input

Output

输出共 行，每行一个非负整数表示答案。

Sample Input

2 1
1 2 3
2 1 3
5

Sample Output

4

只能选用试剂1 和试剂2 配饮料。有两种配法，用量分别为2，3 和3，2 ，每种配法的可口度为2 ，所以答案为4 。

Data Constraint

赛时

一开始想到一个用两个堆来维护的做法。
突然发现好像带个log过不去。
画画柿子突然发现可以差分。
草草打完，用了2个钟。
最后还T了。

题解

考虑差分。
首先，枚举每一种选择情况，一共(n^2)种。
然后对于每一种我们讨论其系数。
大概是长这样的：

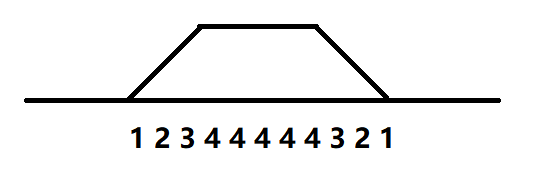
因此，我们只需要考虑分成三段来差分。
首先第递增的，然后是相等的，最后是递减的。
直接差分后做两遍前缀和即可。
注意常数，要稍微优化一下。

标程

#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const long long mo=998244353;
const int maxn=5010;
const int maxm=500010;
const int farr=20000010;

int n,m,tot;
long long a[maxn],l[maxn],r[maxn],q[maxm],sum[farr],ans[maxm];
long long val[maxn*maxn/2],zx[maxn*maxn/2],zd[maxn*maxn/2];

 __attribute__((optimize("-O3")))
int main()
{
	freopen("a.in","r",stdin);
	freopen("a.out","w",stdout);
	scanf("%d%d",&n,&m);
	for (int i=1;i<=n;i++)
	{
		scanf("%lld%lld%lld",&a[i],&l[i],&r[i]);
	}
	int gs=0;
	for (int i=1;i<=n;i++)
	{
		for (int j=i+1;j<=n;j++)
		{
			gs++;
			val[gs]=a[i]*a[j]%mo;
			zx[gs]=l[i]+l[j];
			zd[gs]=r[i]+r[j];
			
			int mid=(zx[gs]+zd[gs])/2;
			int yd=(mid-zx[gs]+1)-min(r[i]-l[i]+1,r[j]-l[j]+1);
			if ((zd[gs]-zx[gs]+1)%2==1)
			{
				sum[zx[gs]]=sum[zx[gs]]+val[gs];
				if (sum[zx[gs]]>10000000000000000) sum[zx[gs]]%=mo;
				sum[mid+1-yd]=(sum[mid+1-yd]-val[gs]+mo);
				if (sum[mid+1-yd]>10000000000000000) sum[mid+1-yd]%=mo;
				sum[mid+1+yd]=(sum[mid+1+yd]-val[gs]+mo);
				if (sum[mid+1+yd]>10000000000000000) sum[mid+1+yd]%=mo;
				sum[zd[gs]+2]=(sum[zd[gs]+2]+val[gs]);
				if (sum[zd[gs]+2]>10000000000000000) sum[zd[gs]+2]%=mo;
			}
			else
			{
				sum[zx[gs]]=sum[zx[gs]]+val[gs];
				if (sum[zx[gs]]>10000000000000000) sum[zx[gs]]%=mo;
				sum[mid+1-yd]=(sum[mid+1-yd]-val[gs]+mo);
				if (sum[mid+1-yd]>10000000000000000) sum[mid+1-yd]%=mo;
				sum[mid+2+yd]=(sum[mid+2+yd]-val[gs]+mo);
				if (sum[mid+2+yd]>10000000000000000) sum[mid+2+yd]%=mo;
				sum[zd[gs]+2]=(sum[zd[gs]+2]+val[gs]);
				if (sum[zd[gs]+2]>10000000000000000) sum[zd[gs]+2]%=mo;
			}
		}
	}
	for (int i=1;i<=farr-1;i++)
	{
		sum[i]=(sum[i-1]+sum[i]+mo)%mo;
	}
	for (int i=1;i<=farr-1;i++)
	{
		ans[i]=(ans[i-1]+sum[i]+mo)%mo;
	}
	for (int i=1;i<=m;i++)
	{
		scanf("%lld",&q[i]);
	}
	for (int i=1;i<=m;i++)
	{
		printf("%lld
",ans[q[i]]);
	}
}