#Description
世界上一共有N个JYY愿意去的城市,分别从1编号到N。JYY选出了K个他一定要乘坐的航班。除此之外,还有M个JYY没有特别的偏好,可以乘坐也可以不乘坐的航班。
一个航班我们用一个三元组(x,y,z)来表示,意义是这趟航班连接城市x和y,并且机票费用是z。每个航班都是往返的,所以JYY花费z的钱,既可以选择从x飞往y,也可以选择从y飞往x。
南京的编号是1,现在JYY打算从南京出发,乘坐所有K个航班,并且最后回到南京,请你帮他求出最小的花费。
#Input
输入数据的第一行包含两个整数N和K;
接下来K行,每行三个整数x,y,z描述必须乘坐的航班的信息,数据保证在这K个航班中,不会有两个不同的航班在同一对城市之间执飞;
第K+2行包含一个整数M;
接下来M行,每行三个整数x,y,z 描述可以乘坐也可以不乘坐的航班信息。
#Output
输出一行一个整数,表示最少的花费。数据保证一定存在满足JYY要求的旅行方案。
#Sample Input
6 3
1 2 1000
2 3 1000
4 5 500
2
1 4 300
3 5 300
#Sample Output
3100
#Data Constraint
对于10%的数据满足N≤4;
对于30%的数据满足N≤ 7;
对于额外30%的数据满足,JYY可以只通过必须乘坐的K个航班从南京出发到达任意一个城市;
对于100%的数据满足2≤N≤13,0≤K≤78,2 ≤M ≤ 200,1 ≤x,y ≤N,1 ≤z ≤ 10^4。
#Hint
样例说明:一个可行的最佳方案为123541。
机票所需的费用为1000+1000+300+500+300=3100。
#题解
题意就是在一个图中,有k条边必须经过,其他边任意经过,从1号点出发,最终回到1号点的最小费用。
这题我第一眼——最小生成树?(太天真了)
第二眼——类似于欧拉回路?(然而我不会)
第三眼——难道是网络流?(拉倒吧)
第四眼——dp?但是有后效性,弃疗吧!
然后,我就不会做了。
结果正解就是一个dp加上类似于欧拉回路的东东再乱搞即可。
听起来简单,搞起来很好搞,但是想到真的是神仙才想得到吧。
我这个凡人算了
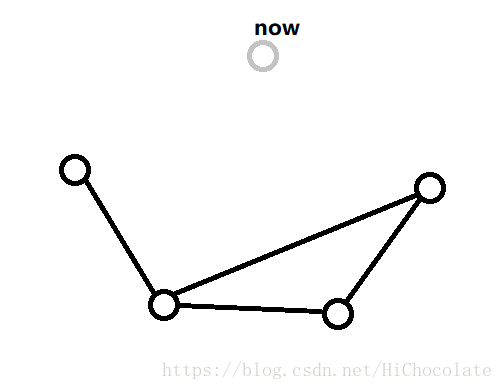
首先,我们先看看画出来的图,我们发现在这个图中会有一个欧拉图,然后,我们就考虑把别的边或点给丢掉,来构成一个欧拉图。
但是这样似乎很难搞,那么我们逆向想想,不如我们就新建一个图,来把边、点给丢进去,变成一个欧拉图,这样似乎很好搞啦。
于是呢,我们就需要一个状态来记录。考虑到n极小,那么就是一个状态压缩。
但是,看到是欧拉图,那么在新的图中的点有两种情况——一是奇点,二是偶点。什么意思?也就是奇点有奇数的边与之相连,偶点就是有偶数的边与之相连。然后还有的点为加入新图,那么就有3种情况——
0:未加入图
1:加入图且为奇点
2:加入图且为偶点
于是现在,我们就看看如何把一个点加入新图中。
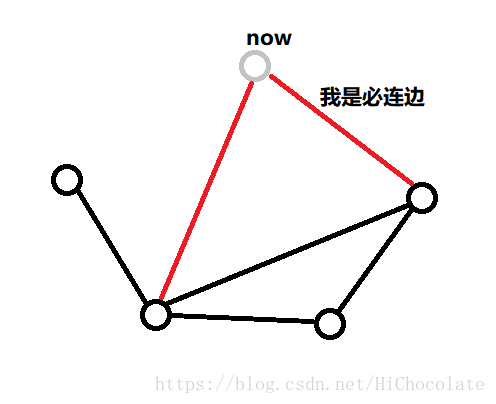
我们就要考虑吧now给连上边
第一种情况:
当有必连边连接,那么就必须连上
然后,我们同时要改变下这个新图的点的奇偶性,即可
第二种情况:
没有必连边时,我们就考虑连一条最近的边。
然后这个显然是可行的。可以以最小的代价把这个点也给连上。
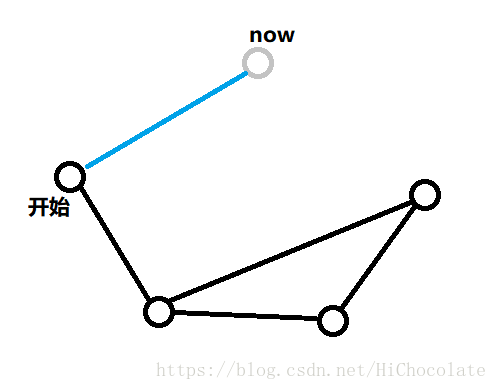
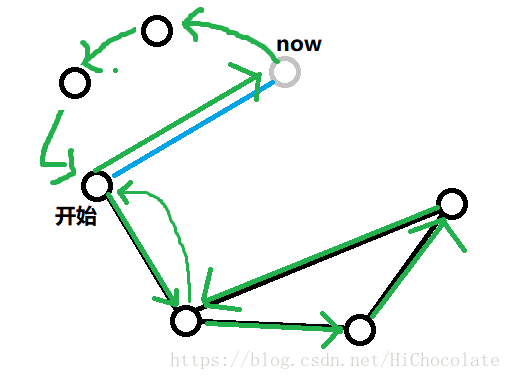
但是,问题来了。正确性能否保证呢?因为以下图的走法,我们会发现开始节点的奇偶性好像会改变。
看看这个走路的方案,好像开始点的奇偶性是奇性,然而,这是个不严谨的欧拉图,这个走路分方案其实是太过于早考虑了,那么我们就先欠下这个账。
先放下那个账,我们可以发现,我们新图中还剩下一些奇点是没有变成偶点的,根据欧拉图,我们就必须把这些奇点给改成偶点才可以行得通,那么我们就把奇点都给拿出来,然后再搞一遍dp,然后用最短路来把这些奇点以最小的费用给匹配出来。
然后就可以吧所有的奇点给变成偶点了。
正确?
没错,因为每次都是两个点之间再连一条最短路的边,那么就代表这两个点之间返回用最小的费用。由于这是个不严谨的欧拉图,那么这个方法也是正确的。
感性理解理解。
欠的旧账——
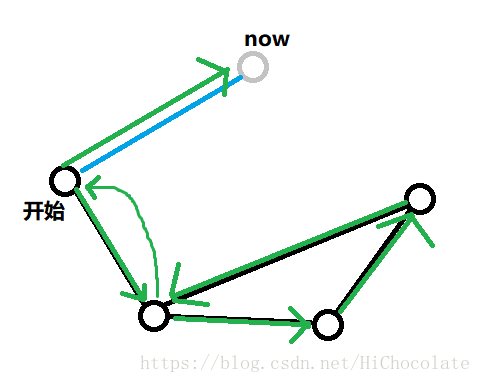
我们看看这个图:
用我们的方法来做,开始点的奇偶性为奇性,然后呢,我们就可以根据我们刚刚讲的方法来把这个开始点与另一个点匹配,那么也就可能走了一条重复的边,由于刚才说这样是正确的,那么这个走法也是正确的。
也就是说,我们在加入点时,不考虑它走不走重复边,只有在最后把奇点匹配时才从真正意义上来走重复边。
理解理解。
然后你就会了。
代码:
uses math;
var
i,j,k,l,o,n,m,zs,answer,tot,tot1,maxx,zy,gs,add,p:longint;
x,y,z,x1,y1,z1,tov,next,last,a,b:array[1..10000] of longint;
map:array[1..13,1..13] of longint;
f:array[0..1594323] of longint;
pp:array[0..13] of longint;
mi,mi2,apple:array[0..14] of longint;
bz:array[1..14] of boolean;
dp:array[0..8191] of longint;
flag,flag1:boolean;
procedure insert(x,y:longint);
begin
inc(tot);
tov[tot]:=y;
next[tot]:=last[x];
last[x]:=tot;
end;
begin
fillchar(map,sizeof(map),127);
maxx:=map[1,1];
readln(zs,n);
for i:=1 to n do
begin
readln(x[i],y[i],z[i]);
insert(x[i],y[i]);
insert(y[i],x[i]);
bz[x[i]]:=true;
bz[y[i]]:=true;
x[n+i]:=y[i];
y[n+i]:=x[i];
z[n+i]:=z[i];
map[x[i],y[i]]:=min(z[i],map[x[i],y[i]]);
map[y[i],x[i]]:=map[x[i],y[i]];
answer:=answer+z[i];
end;
readln(m);
for i:=1 to m do
begin
readln(x1[i],y1[i],z1[i]);
map[x1[i],y1[i]]:=min(map[x1[i],y1[i]],z1[i]);
map[y1[i],x1[i]]:=map[x1[i],y1[i]];
end;
for k:=1 to zs do
begin
for i:=1 to zs do
begin
if i<>k then
for j:=1 to zs do
begin
if (i<>j) and (k<>j) then
begin
if (map[i,k]<maxx) and (map[k,j]<maxx) then
map[i,j]:=min(map[i,j],map[i,k]+map[k,j]);
end;
end;
end;
end;
mi[1]:=1;
mi2[1]:=1;
for i:=2 to zs+1 do
begin
mi[i]:=mi[i-1]*3;
mi2[i]:=mi2[i-1]*2;
end;
fillchar(f,sizeof(f),127);
f[2]:=0;
for i:=1 to mi[zs+1]-1 do
begin
zy:=i;
flag1:=true;
for j:=1 to zs do
begin
apple[j]:=i mod mi[j+1] div mi[j];
end;
for j:=1 to zs do
begin
zy:=i;
if ((apple[j])=0) and (bz[j]) then
begin
flag1:=false;
flag:=true;
gs:=0;
k:=last[j];
while k>0 do
begin
l:=apple[tov[k]];
if l>0 then
begin
flag:=false;
if l=1 then zy:=zy+mi[tov[k]]
else
if l=2 then zy:=zy-mi[tov[k]];
inc(gs);
end;
k:=next[k];
end;
if flag then
begin
p:=j;
for k:=1 to zs do
begin
if apple[k]>0 then
begin
if map[j,k]<map[j,p] then
begin
p:=k;
end;
end;
end;
zy:=zy+mi[j];
l:=i mod mi[p+1] div mi[p];
if l=1 then zy:=zy+mi[p]
else
if l=2 then zy:=zy-mi[p];
if map[j,p]<maxx then
f[zy]:=min(f[zy],f[i]+map[j,p]);
end
else
begin
if gs mod 2=0 then gs:=2
else gs:=1;
zy:=zy+gs*mi[j];
f[zy]:=min(f[zy],f[i]);
end;
end;
end;
end;
for i:=1 to mi2[zs+1]-1 do
begin
j:=0;
for k:=1 to zs do
begin
if i and mi2[k]>0 then
begin
j:=k;
break;
end;
end;
dp[i]:=maxx;
for k:=1 to zs do
begin
if (i and mi2[k]>0) and (k<>j) then
begin
dp[i]:=min(dp[i],dp[i-mi2[k]-mi2[j]]+map[j,k]);
end;
end;
end;
tot1:=mi[zs+1]-1;
for i:=1 to zs do
begin
if not bz[i] then
begin
tot1:=tot1-mi[i]*2;
end;
end;
for i:=2 to mi[zs+1]-1 do
begin
if f[i]=maxx then continue;
for j:=1 to zs do
begin
apple[j]:=i mod mi[j+1] div mi[j];
end;
zy:=i;
flag1:=true;
for j:=1 to zs do
begin
zy:=i;
if ((apple[j])=0) and (bz[j]) then
begin
flag1:=false;
break;
end;
end;
if flag1 then
begin
pp[0]:=0;
add:=0;
zy:=0;
for j:=1 to zs do
begin
if (apple[j])=1 then
begin
inc(pp[0]);
pp[pp[0]]:=j;
zy:=zy+mi2[j];
end;
end;
if pp[0] mod 2=1 then continue;
add:=dp[zy];
if add<maxx then
begin
f[tot1]:=min(f[tot1],f[i]+add);
end;
end;
end;
writeln(f[tot1]+answer);
end.