1. 问题描述
设有n个物体和一个背包,物体i的重量为wi价值为pi ,背包的载荷为M, 若将物体i(1<= i <=n)装入背包,则有价值为pi . 目标是找到一个方案, 使得能放入背包的物体总价值最高.
设N=3, W=(16,15,15), P=(45,25,25), C=30(背包容量)
2. 队列式分支限界法
可以通过画分支限界法状态空间树的搜索图来理解具体思想和流程
每一层按顺序对应一个物品放入背包(1)还是不放入背包(0)
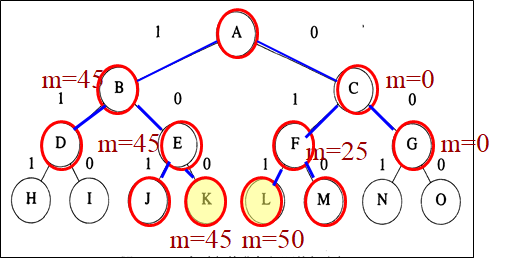
步骤:
① 用一个队列存储活结点表,初始为空
② A为当前扩展结点,其儿子结点B和C均为可行结点,将其按从左到右顺序加入活结点队列,并舍弃A。
③ 按FIFO原则,下一扩展结点为B,其儿子结点D不可行,舍弃;E可行,加入。舍弃B
④ C为当前扩展结点,儿子结点F、G均为可行结点,加入活结点表,舍弃C
⑤ 扩展结点E的儿子结点J不可行而舍弃;K为可行的叶结点,是问题的一个可行解,价值为45
⑥ 当前活结点队列的队首为F, 儿子结点L、M为可行叶结点,价值为50、25
⑦ G为最后一个扩展结点,儿子结点N、O均为可行叶结点,其价值为25和0
⑧ 活结点队列为空,算法结束,其最优值为50
注:活结点就是不可再进行扩展的节点,也就是两个儿子还没有全部生成的节点
3. 优先队列式分支限界法
3.1 以活结点价值为优先级准则
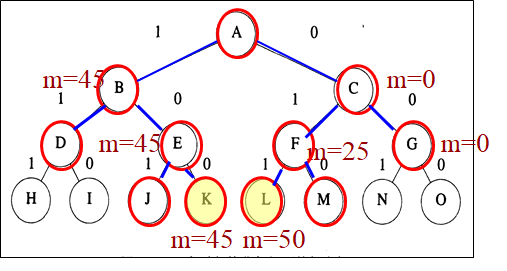
步骤:
① 用一个极大堆表示活结点表的优先队列,其优先级定义为活结点所获得的价值。初始为空。
② 由A开始搜索解空间树,其儿子结点B、C为可行结点,加入堆中,舍弃A。
③ B获得价值45,C为0. B为堆中价值最大元素,并成为下一扩展结点。
④ B的儿子结点D是不可行结点,舍弃。E是可行结点,加入到堆中。舍弃B。
⑤ E的价值为45,是堆中最大元素,为当前扩展结点。
⑥ E的儿子J是不可行叶结点,舍弃。K是可行叶结点,为问题的一个可行解价值为45。
⑦ 继续扩展堆中唯一活结点C,直至存储活结点的堆为空,算法结束。
⑧ 算法搜索得到最优值为50,最优解为从根结点A到叶结点L的路径(0,1,1)。
3.2 以限界函数为优先级准则
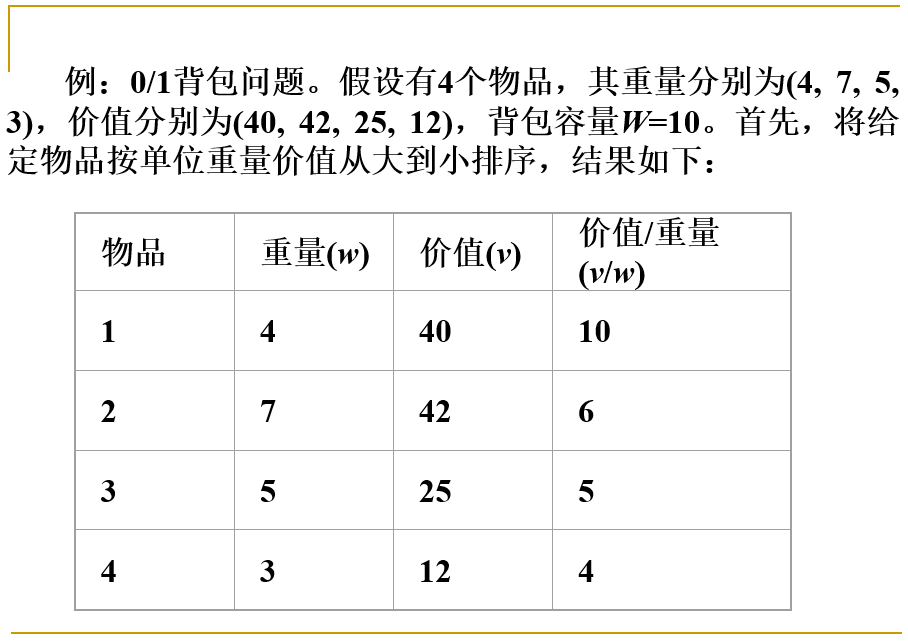
应用贪心法求得近似解为(1, 0, 0, 0),获得的价值为40,这可以作为0/1背包问题的下界。
如何求得0/1背包问题的一个合理的上界呢?考虑最好情况,背包中装入的全部是第1个物品且可以将背包装满,则可以得到一个非常简单的上界的计算方法:
b=W×(v1/w1)=10×10=100。于是,得到了目标函数的界[40, 100]。
所以我们定义限界函数为:
![]()
再来画状态空间树的搜索图:
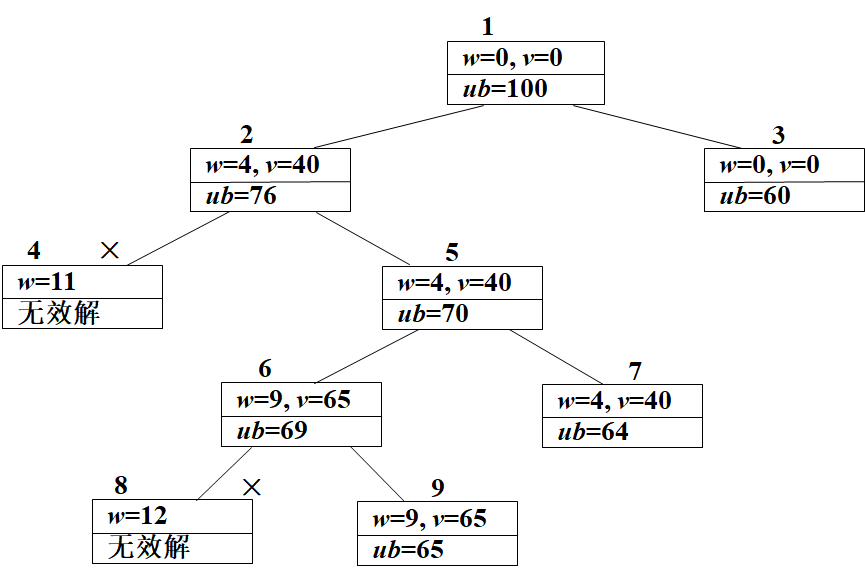
步骤:
① 在根结点1,没有将任何物品装入背包,因此,背包的重量和获得的价值均为0,根据限界函数计算结点1的目标函数值为10×10=100;
② 在结点2,将物品1装入背包,因此,背包的重量为4,获得的价值为40,目标函数值为40 + (10-4)×6=76,将结点2加入待处理结点表PT中;在结点3,没有将物品1装入背包,因此,背包的重量和获得的价值仍为0,目标函数值为10×6=60,将结点3加入表PT中;
③ 在表PT中选取目标函数值取得极大的结点2优先进行搜索;
④ 在结点4,将物品2装入背包,因此,背包的重量为11,不满足约束条件,将结点4丢弃;在结点5,没有将物品2装入背包,因此,背包的重量和获得的价值与结点2相同,目标函数值为40 + (10-4)×5=70,将结点5加入表PT中;
⑤ 在表PT中选取目标函数值取得极大的结点5优先进行搜索;
⑥ 在结点6,将物品3装入背包,因此,背包的重量为9,获得的价值为65,目标函数值为65 + (10-9)×4=69,将结点6加入表PT中;在结点7,没有将物品3装入背包,因此,背包的重量和获得的价值与结点5相同,目标函数值为40 + (10-4)×4=64,将结点6加入表PT中;
⑦ 在表PT中选取目标函数值取得极大的结点6优先进行搜索;
⑧ 在结点8,将物品4装入背包,因此,背包的重量为12,不满足约束条件,将结点8丢弃;在结点9,没有将物品4装入背包,因此,背包的重量和获得的价值与结点6相同,目标函数值为65;
⑨ 由于结点9是叶子结点,同时结点9的目标函数值是表PT中的极大值,所以,结点9对应的解即是问题的最优解,搜索结束。
总结:
★ 剪枝函数给出每个可行结点相应的子树可能获得的最大价值的上界。
★ 如这个上界不会比当前最优值更大,则可以剪去相应的子树。
★ 也可将上界函数确定的每个结点的上界值作为优先级,以该优先级的非增序抽取当前扩展结点。由此可快速获得最优解。