给袜子颜色的队列
进行区间询问[l,r]
输出该区间内随机抽两次抽到相同颜色袜子的概率
莫队算法可用于解决一类可离线且在得到区间[l,r]的答案后
可以O(1)或O(log2 n)时间内求出区间[l-1,r],[l+1,r],[l,r+1],[l,r-1]的答案的问题
两者区间只差了一个元素(此题为一个颜色的袜子的数量++或--)
只考虑这个元素所带来的差异,进行计算转移
方法
1.排序时以左端点所在的块为第一关键字,以右端点为第二关键字
即对于两个询问,若在其左端点在同块,那么就排序右端点,若左端点不在同块,就将左端点作为关键字排序
2.从左往右处理询问(离线)
3.不断调整l,r的位置解决询问
设每种颜色袜子个数为a,b,c……

化简后得
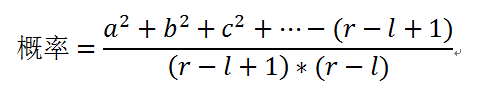
转化为求每个区间内各个颜色袜子的数目的平方和
1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 #define ll long long 7 using namespace std; 8 const int N=50010; 9 struct qiu 10 { 11 int l,r,tim; //tim存储是第几个询问 12 ll A,B; //A为分子,B为分母 13 }q[N]; 14 ll gcd(ll a,ll b) //输出要求最简分数 15 { 16 if(b==0) return a; 17 else return gcd(b,a%b); 18 } 19 int n,m,col[N],K,bl[N]; 20 ll sum[N],ans; 21 bool cmp1(qiu a,qiu b) //双关键字排序 22 { 23 if(bl[a.l]==bl[b.l]) return a.r<b.r; 24 else return a.l<b.l; 25 } 26 bool cmp2(qiu a,qiu b) 27 { 28 return a.tim<b.tim; //最后按询问顺序输出 29 } 30 void aa(int x,int add) //每次改变一个颜色袜子的数量++或-- 31 { 32 ans-=sum[col[x]]*sum[col[x]]; 33 sum[col[x]]+=add; 34 ans+=sum[col[x]]*sum[col[x]]; 35 } 36 int main() 37 { 38 scanf("%d%d",&n,&m); 39 K=sqrt(n); 40 for(int i=1;i<=n;i++) 41 { 42 scanf("%d",&col[i]); 43 bl[i]=i/K+1; 44 } 45 for(int i=1;i<=m;i++) 46 { 47 scanf("%d%d",&q[i].l,&q[i].r); 48 q[i].tim=i; 49 } 50 sort(q+1,q+m+1,cmp1); 51 int l=1,r=0; 52 for(int i=1;i<=m;i++) 53 { 54 while(l<q[i].l) 55 { 56 aa(l,-1); 57 l++; 58 } 59 while(l>q[i].l) 60 { 61 aa(l-1,1); 62 l--; 63 } 64 while(r<q[i].r) 65 { 66 aa(r+1,1); 67 r++; 68 } 69 while(r>q[i].r) 70 { 71 aa(r,-1); 72 r--; 73 } 74 if(q[i].l==q[i].r) 75 { 76 q[i].A=0; 77 q[i].B=1; 78 continue; 79 } 80 q[i].A=ans-(q[i].r-q[i].l+1); 81 q[i].B=1LL*(q[i].r-q[i].l+1)*(q[i].r-q[i].l); 82 ll gg=gcd(q[i].A,q[i].B); 83 q[i].A/=gg; 84 q[i].B/=gg; 85 } 86 sort(q+1,q+m+1,cmp2); 87 for(int i=1;i<=m;i++)printf("%lld/%lld ",q[i].A,q[i].B); 88 return 0; 89 }