L1范数损失函数,也被称为最小绝对值偏差(LAD),最小绝对值误差(LAE)
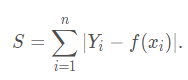
L2范数损失函数,也被称为最小平方误差(LSE)

| L2损失函数 | L1损失函数 |
|---|---|
| 不是非常的鲁棒(robust) | 鲁棒 |
| 稳定解 | 不稳定解 |
| 总是一个解 | 可能多个解 |
鲁棒性
最小绝对值偏差之所以是鲁棒的,是因为它能处理数据中的异常值。如果需要考虑任一或全部的异常值,那么最小绝对值偏差是更好的选择。
L2范数将误差平方化(如果误差大于1,则误差会放大很多),模型的误差会比L1范数来得大,因此模型会对这个样本更加敏感,这就需要调整模型来最小化误差。如果这个样本是一个异常值,模型就需要调整以适应单个的异常值,这会牺牲许多其它正常的样本,因为这些正常样本的误差比这单个的异常值的误差小。
稳定性
最小绝对值偏差方法的不稳定性意味着,对于数据集的一个小的水平方向的波动,回归线也许会跳跃很大。
相反地,最小平方法的解是稳定的,因为对于一个数据点的任何微小波动,回归线总是只会发生轻微移动
总结
MSE对误差取了平方,如果存在异常值,那么这个MSE就很大。
MAE更新的梯度始终相同,即使对于很小的值,梯度也很大,可以使用变化的学习率。MSE就好很多,使用固定的学习率也能有效收敛。
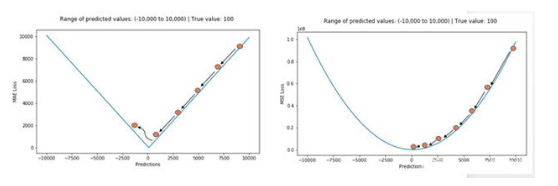
总而言之,处理异常点时,L1损失函数更稳定,但它的导数不连续,因此求解效率较低。L2损失函数对异常点更敏感,但通过令其导数为0,可以得到更稳定的封闭解。
Huber
l1和l2都存在的问题:
若数据中90%的样本对应的目标值为150,剩下10%在0到30之间。
那么使用MAE作为损失函数的模型可能会忽视10%的异常点,而对所有样本的预测值都为150,因为模型会按中位数来预测;
MSE的模型则会给出很多介于0到30的预测值,因为模型会向异常点偏移。
这些情况下最简单的办法是对目标变量进行变换。而另一种办法则是换一个损失函数,这就引出了下面要讲的第三种损失函数,即Huber损失函数。
Huber损失,平滑的平均绝对误差
Huber损失对数据中的异常点没有平方误差损失那么敏感。
本质上,Huber损失是绝对误差,只是在误差很小时,就变为平方误差。误差降到多小时变为二次误差由超参数δ(delta)来控制。当Huber损失在[0-δ,0+δ]之间时,等价为MSE,而在[-∞,δ]和[δ,+∞]时为MAE。
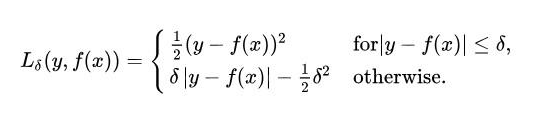
Huber损失结合了MSE和MAE的优点,对异常点更加鲁棒。