在看完这两个视频之后萌生出了我也来写个程序模拟下的想法,看了下简介里面好像没给出源码, up 用的是 c/cpp 写的,笔者人生苦短,就用 python 实现了,效率确实要差很多,下面的很多过程和思路都是参考了 up 视频完成的
https://www.bilibili.com/video/BV1MZ4y1p7Ff
https://www.bilibili.com/video/BV1Nk4y1B78W视频中首先表示公示概率是包含了保底的综合概率,因此需要反推原始的单抽概率,因此使用几何分布求出货时所消耗补给卡数量的期望,设单抽的概率为 p
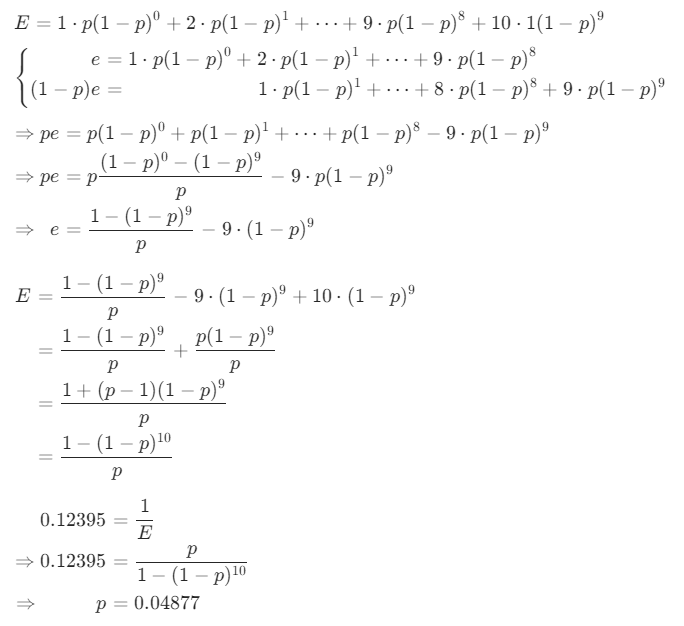
最后一步求解是使用 Mathematica 求解的,排除掉复数解,概率 p 则为 0.04877

因此可知四星装备的综合概率与原始单抽概率的比值为 (12.395 / 4.877) ,根据游戏公告,四星装备和UP四星装备的概率呈比例,因此可以直接直接乘以系数得到所有的原始概率
| 综合概率 | 单抽概率 | ||
| 精准/扩充 | 四星装备 | 12.395% | 4.877% |
| 精准 | 四星武器 | 4.958% | 1.951% |
| 精准 | 四星圣痕 | 7.437% | 2.962% |
| 精准 | UP武器 | 2.479% | 0.975% |
| 精准 | UP圣痕 | 1.240% | 0.488% |
| 扩充 | 四星武器 | 4.580% | 1.802% |
| 扩充 | 四星圣痕 | 7.815% | 3.075% |
| 扩充 | UP武器 | 1.831% | 0.720% |
| 扩充 | UP圣痕 | 0.916% | 0.360% |
有了概率之后只需要模拟抽卡逻辑进行大量抽样即可,程序已开源在 GITHUB ,以下为笔者对精准和扩充卡池各进行 12 亿人次抽样得到的结果。目前只完成了基础的框架,两个卡池均使用许愿机制且均抽齐四件套。结论和 up 视频中的有些许不同,望发现 bug 的舰长能帮忙指出,图中数据的分析可以参考 up 的视频
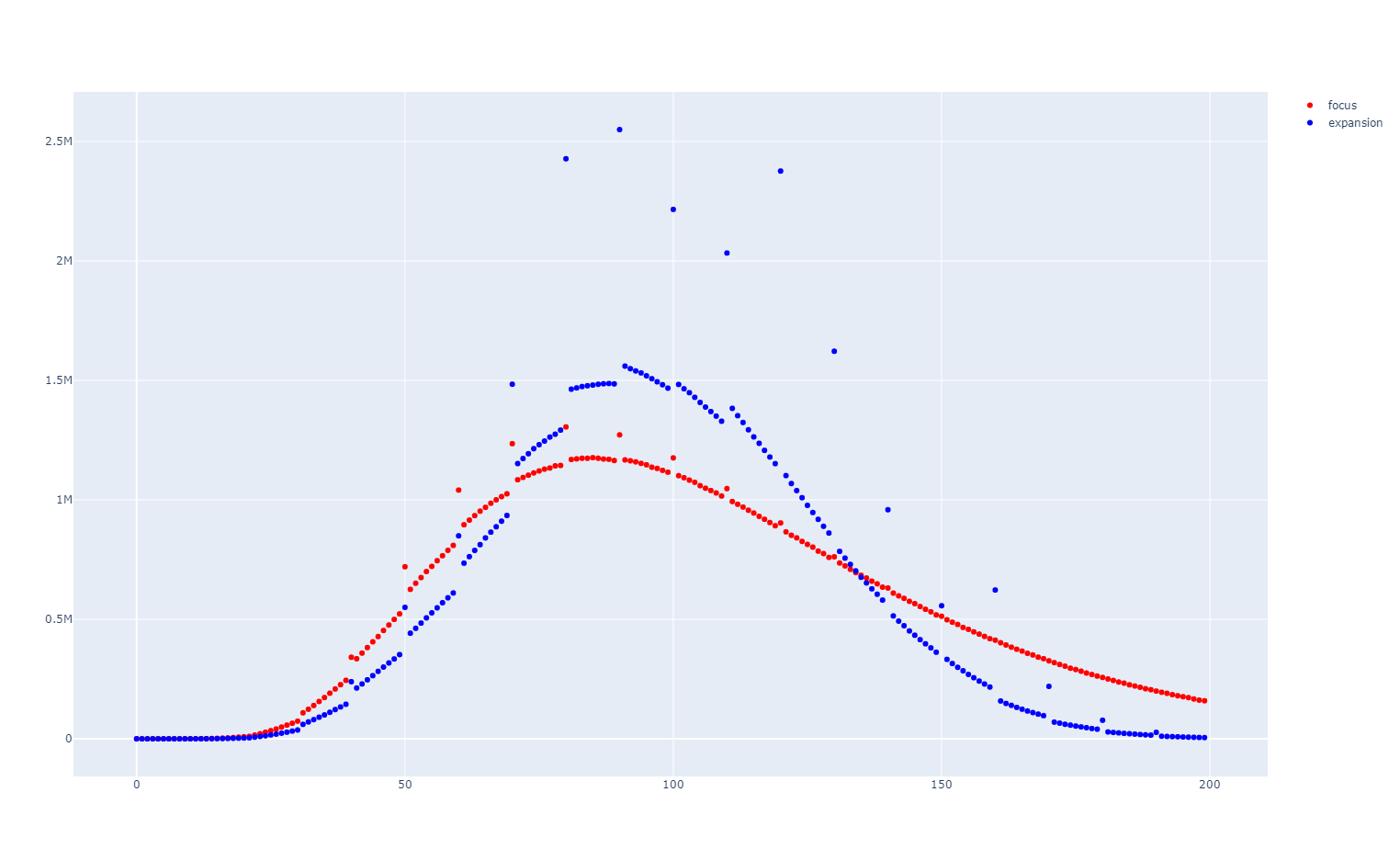
精准补给平均数: 103.27446421087244
扩充补给平均数: 99.35898730322731
精准补给中位数: 99
扩充补给中位数: 98
开源链接
https://github.com/Pyrokine/honkai_impact_3_gacha_simulator