本文算是对其他人答案的解释吧
根据石头数量(即数组长度N)生成NxN的矩阵,每个位置 [i, j] 表示的含义为 i 到 j 的所有合成方式中的最小值
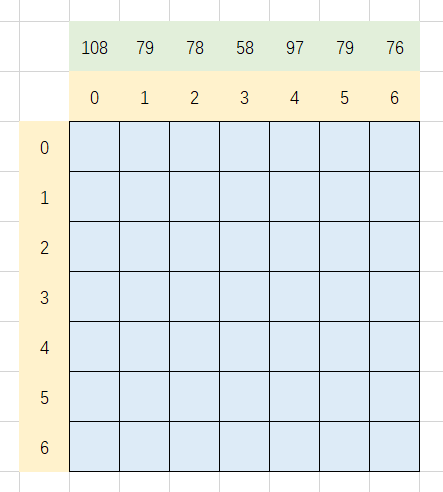
假设数据如上图所示,合成为三个一合并,那么,只有下图中深蓝色区域为有效区域,其他位置赋0。以第一行为例,0-0和0-1为无效合并,0-2为第一个有效的合并,直到0-6都是有效合并,第四行唯一有效的为4-6,这也是长度为3时最后一个有效的合并

那么,需要确定计算顺序,最后一次计算是 0-6 全部合并,即填入右上角那个格子,合并三个石头,这三个中其中两个可以是由其他石头合并来的,如下图左,也可以其中一个是由其他合并来的,另外两个来自最初的石头,如下图右,当然,如果石头更多,则可以全都来自于合并后的石头

但如果是K个合并,则问题会变得很复杂,因此将合并简化为左侧石头和右侧石头合并,并保证每侧都是有效的,如果将左侧定义为1个石头(原始的1个或者合并成后的一个),右侧为 K-1 个石头,这样左侧就有固定解了,而右侧长度小于原长度,即变为子问题,即
step = K - 1, left = 1 + n * step ①
两侧的数量:[left, N - left] ② n取所有可能的值,例如在合并长度为7时,所有子问题为 [1, 6]、[3, 4]、[5, 2] ③
注:式①变形可得(left - 1) / (K - 1) = n,意为该长度有效,这也是最开始用来检测命题是否有效的公式
这样就将问题拆解为重复子问题了,子问题为每个区间 [i, j] 的最小合并值,然后对②的所有子问题求最小值,即两侧分别为 1 个和 6 个、 3 个和 4 个、 5 个和 2 个时,哪种合并能得到最小值,然后子问题递归求解,而递归的逆运算即为递推(动态规划)了,dp 不会求解重复子问题,自然速度也快一些
再对③推一层,假设 [3, 4] 是最小的解,这里面 3 是能够通过同样方式计算出来的,4 就有点不同,拆开是 [1, 3] 和 [3, 1] ,可以理解为一个存在解的石头 3 和一个多余的石头 1 ,计算时就用存在解的 3 的合并值额外加那 1 个石头的值即可,不存在额外的加分
而额外加分指的是题目中的合并后需要将当前合累加进合并值,即 i 到 j 所有值累加后加到合并值上,观察最小子问题可发现,可以换一个角度理解什么时候需要额外加分,即假设 K = 5 ,已经存在一组合并好的石头,然后额外多 1 个、 2 个......这并不会额外加分,只用累加每个的值即可,如果这个是命题,则直接判否,直到额外多了 4 个,可以和最开始合并好的石头组成 5 个时,即可额外加分
因此,在后续每层计算时,采用相同的思路,如果没有达到倍数时,就单纯找到最小值,然后累加,当达到倍数时,额外加分,其中某些子问题不是真命题,但是有实际意义
附上代码
https://www.jiuzhang.com/solution/minimum-cost-to-merge-stones/#tag-other-lang-python
1 class Solution: 2 def mergeStones(self, stones, K): 3 n = len(stones) 4 5 if (n - 1) % (K - 1) != 0: 6 return -1 7 8 f = [[0 for _ in range(n)] for _ in range(n)] 9 10 prefix = [0 for _ in range(n + 1)] 11 for i in range(n): 12 prefix[i + 1] = prefix[i] + stones[i] 13 14 for l in range(K - 1, n): 15 for i in range(n - l): 16 j = i + l 17 f[i][j] = float('inf') 18 for m in range(i, j, K - 1): 19 f[i][j] = min(f[i][j], f[i][m] + f[m + 1][j]) 20 if (j - i) % (K - 1) == 0: 21 f[i][j] += prefix[j + 1] - prefix[i] 22 23 return f[0][n - 1]