提示:非O(n)解,另一种直观的理解
最终结果满足几个条件:
1、水面是水平的
2、高度时离散的
3、当确定x1、x2为能维持当前水平面高度的最外侧两个边,则不存在更外侧的边使得在当前水平面高度下水箱面积更大
4、最少有两个边(高度可以为0)
5、假设水平面高度为a时,可以将大于a的边看作高度为a
那么,程序思路就很简单了,(按已有的边)从最高的边开始往低遍历,然后所有高度更高的边都看作当前高度的边,之后求当前高度所有边中扩张到最大宽度的两个边,然后更新面积(笔者是记录所有面积然后max,效率是相同的,写的简洁些)
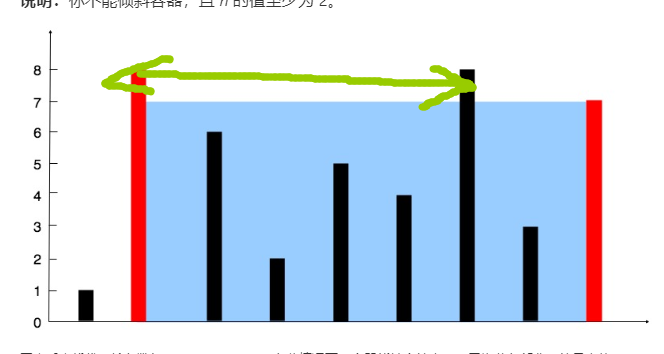
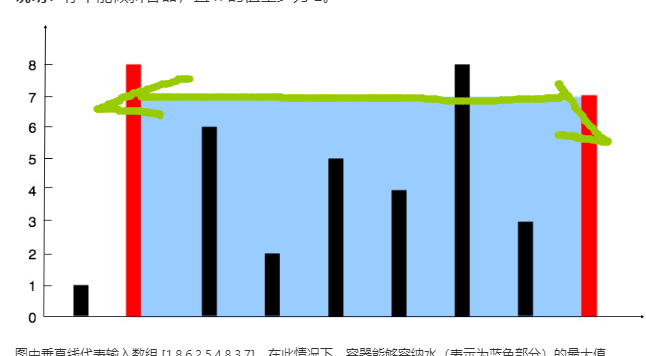
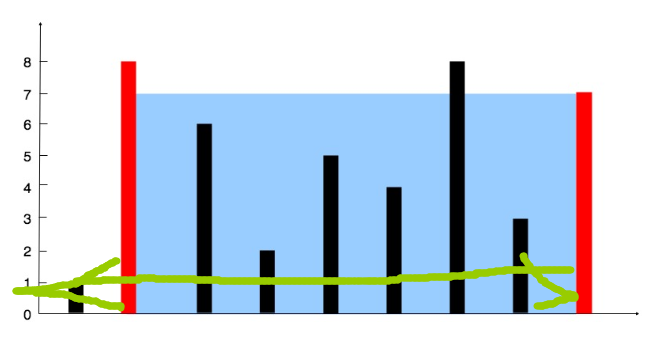
一个小trick,为了降低运算量,在使用归并排序时,在高度相同时对相同高度的边按出现顺序从左到右排序,那么若两个相邻的边高度不同时,则一定是上一层的最右侧边和下一层的最左侧边,更新高度然后继续遍历即可
效率为归并排序o(nlogn)和一遍遍历o(n),时间复杂度稍高,但是很好理解,并且不需要过多推导
1 class Solution(object): 2 def maxArea(self, height): 3 arry = [] 4 for i in range(len(height)): 5 arry.append([height[i], i]) 6 arry = sorted(arry, key=lambda x: (-x[0], x[1])) 7 arry.append([0, 0]) 8 # print(arry) 9 aa = [arry[0][1], arry[0][1]] 10 bb = [] 11 temp = arry[0][0] 12 len_arry = len(arry) - 1 13 for i in range(0, len_arry): 14 if temp != arry[i + 1][0]: 15 if arry[i][1] > aa[1]: 16 aa[1] = arry[i][1] 17 bb.append(arry[i][0] * (aa[1] - aa[0])) 18 if arry[i + 1][1] < aa[0]: 19 aa[0] = arry[i + 1][1] 20 bb.append(arry[i + 1][0] * (aa[1] - aa[0])) 21 temp = arry[i + 1][0] 22 # print(bb) 23 if bb: 24 return max(bb) 25 else: 26 return 0