数据结构开发(25)：二叉树中属性操作、层次遍历与典型遍历

0.目录

1.二叉树的比较与相加

2.二叉树的线索化实现

3.二叉树的经典面试题分析

• 3.1 单度结点删除
• 3.2 中序线索化二叉树

4.小结

1.二叉树的比较与相加

二叉树的克隆操作：

• SharedPointer< BTree<T> > clone() const
  1. 克隆当前树的一份拷贝
  2. 返回值为堆空间中的一棵新二叉树 ( 与当前树相等 )

二叉树的克隆：

• 定义功能：clone(node)
  1. 拷贝 node 为根结点的二叉树 ( 数据元素在对应位置相等 )

在BTree.h中实现二叉树的克隆操作：

protected:
    BTreeNode<T>* clone(BTreeNode<T>* node) const
    {
        BTreeNode<T>* ret = NULL;

        if( node != NULL )
        {
            ret = BTreeNode<T>::NewNode();

            if( ret != NULL )
            {
                ret->value = node->value;

                ret->left = clone(node->left);
                ret->right = clone(node->right);

                if( ret->left != NULL )
                {
                    ret->left->parent = ret;
                }

                if( ret->right != NULL )
                {
                    ret->right->parent = ret;
                }
            }
            else
            {
                THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create new node ...");
            }
        }

        return ret;
    }
public:
    SharedPointer< BTree<T> > clone() const
    {
        BTree<T>* ret = new BTree<T>();

        if( ret != NULL )
        {
            ret->m_root = clone(root());
        }
        else
        {
            THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create new tree ...");
        }

        return ret;
    }

二叉树比较操作的定义：

• 判断两棵二叉树中的数据元素是否对应相等
  1. bool operator == (const BTree<T>& btree)
  2. bool operator != (const BTree<T>& btree)

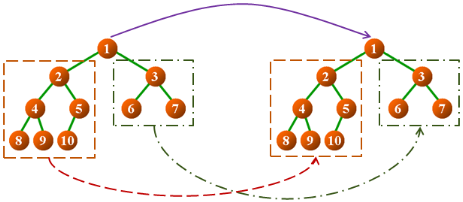
二叉树的比较：

• 定义功能：equal(lh, rh)
  1. 判断 Ih 为根结点的二叉树与 rh 为根结点的二叉树是否相等

在BTree.h中实现二叉树的比较操作：

protected:
    bool equal(BTreeNode<T>* lh, BTreeNode<T>* rh) const
    {
        if( lh == rh )
        {
            return true;
        }
        else if( (lh != NULL) && (rh != NULL) )
        {
            return (lh->value == rh->value) && equal(lh->left, rh->left) && equal(lh->right, rh->right);
        }
        else
        {
            return false;
        }
    }
public:
    bool operator == (const BTree<T>& btree)
    {
        return equal(root(), btree.root());
    }

    bool operator != (const BTree<T>& btree)
    {
        return !(*this == btree);
    }

统一mian.cpp测试：

#include <iostream>
#include "BTree.h"

using namespace std;
using namespace StLib;

int main()
{
    BTree<int> bt;
    BTreeNode<int>* n = NULL;

    bt.insert(1, NULL);

    n = bt.find(1);
    bt.insert(2, n);
    bt.insert(3, n);

    n = bt.find(2);
    bt.insert(4, n);
    bt.insert(5, n);

    n = bt.find(4);
    bt.insert(8, n);
    bt.insert(9, n);

    n = bt.find(5);
    bt.insert(10, n);

    n = bt.find(3);
    bt.insert(6, n);
    bt.insert(7, n);

    SharedPointer< BTree<int> > btClone = bt.clone();

    int a[] = {8, 9, 10, 6, 7};

    cout << "Clone: " << endl;
    for(int i=0; i<5; i++)
    {
        TreeNode<int>* node = btClone->find(a[i]);

        while( node )
        {
            cout << node->value << " ";
            node = node->parent;
        }
        cout << endl;
    }
    cout << endl;

    cout << "Old BTree: " << endl;
    for(int i=0; i<5; i++)
    {
        TreeNode<int>* node = bt.find(a[i]);

        while( node )
        {
            cout << node->value << " ";
            node = node->parent;
        }
        cout << endl;
    }
    cout << endl;

    cout << "bt == *btClone : " << (bt == *btClone) << endl;

    return 0;
}

运行结果为：

Clone: 
8 4 2 1 
9 4 2 1 
10 5 2 1 
6 3 1 
7 3 1 

Old BTree: 
8 4 2 1 
9 4 2 1 
10 5 2 1 
6 3 1 
7 3 1 

bt == *btClone : 1

二叉树的相加操作：

• SharedPointer< BTree<T> > add(const BTree<T>& btree) const
  1. 将当前二叉树与参数 btree 中的数据元素在对应位置处相加
  2. 返回值 ( 相加的结果 ) 为堆空间中的一棵新二叉树

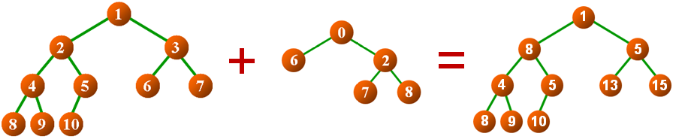
二叉树的加法：

• 定义功能：add(Ih, rh)
  1. 将 Ih 为根结点的二叉树与 rh 为根结点的二叉树相加

在BTree.h中实现二叉树的相加操作：

protected:
    BTreeNode<T>* add(BTreeNode<T>* lh, BTreeNode<T>* rh) const
    {
        BTreeNode<T>* ret = NULL;

        if( (lh == NULL) && (rh != NULL) )
        {
            ret = clone(rh);
        }
        else if( (lh != NULL) && (rh == NULL) )
        {
            ret = clone(lh);
        }
        else if( (lh != NULL) && (rh != NULL) )
        {
            ret = BTreeNode<T>::NewNode();

            if( ret != NULL )
            {
                ret->value = lh->value + rh->value;

                ret->left = add(lh->left, rh->left);
                ret->right = add(lh->right, rh->right);

                if( ret->left != NULL )
                {
                    ret->left->parent = ret;
                }

                if( ret->right != NULL )
                {
                    ret->right->parent = ret;
                }
            }
            else
            {
                THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create new node ...");
            }
        }

        return ret;
    }
public:
    SharedPointer< BTree<T> > add(const BTree<T>& btree) const
    {
        BTree<T>* ret = new BTree<T>();

        if( ret != NULL )
        {
            ret->m_root = add(root(), btree.root());
        }
        else
        {
            THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create new tree ...");
        }

        return ret;
    }

mian.cpp测试：

#include <iostream>
#include "BTree.h"

using namespace std;
using namespace StLib;

int main()
{
    BTree<int> bt;
    BTreeNode<int>* n = NULL;

    bt.insert(1, NULL);

    n = bt.find(1);
    bt.insert(2, n);
    bt.insert(3, n);

    n = bt.find(2);
    bt.insert(4, n);
    bt.insert(5, n);

    n = bt.find(4);
    bt.insert(8, n);
    bt.insert(9, n);

    n = bt.find(5);
    bt.insert(10, n);

    n = bt.find(3);
    bt.insert(6, n);
    bt.insert(7, n);


    BTree<int> nbt;

    nbt.insert(0, NULL);

    n = nbt.find(0);
    nbt.insert(6, n);
    nbt.insert(2, n);

    n = nbt.find(2);
    nbt.insert(7, n);
    nbt.insert(8, n);

    SharedPointer< BTree<int> > r = bt.add(nbt);

    int a[] = {8, 9, 10, 13, 5};

    cout << "Add result: " << endl;
    for(int i=0; i<5; i++)
    {
        TreeNode<int>* node = r->find(a[i]);

        while( node )
        {
            cout << node->value << " ";
            node = node->parent;
        }
        cout << endl;
    }
    cout << endl;

    SharedPointer< Array<int> > tr = r->traversal(PreOrder);

    cout << "先序遍历：" << endl;
    for(int i=0; i<(*tr).length(); i++)
    {
        cout << (*tr)[i] << " ";
    }
    cout << endl;

    return 0;
}

运行结果为：

Add result: 
8 1 
9 4 8 1 
10 5 8 1 
13 5 1 
5 8 1 

先序遍历：
1 8 4 8 9 5 10 5 13 15 

2.二叉树的线索化实现

什么是线索化二叉树？

• 将二叉树转换为双向链表的过程 ( 非线性 → 线性 )
• 能够反映某种二叉树的遍历次序 ( 结点的先后访问次序 )
  1. 利用结点的 right 指针指向遍历中的后继结点
  2. 利用结点的 left 指针指向遍历中的前驱结点

如何对二叉树进行线索化？
思维过程：

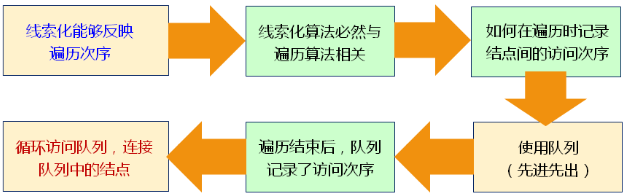
二叉树的线索化：

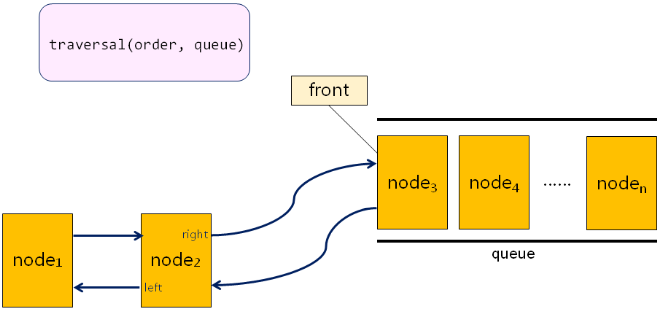
本节目标：

• 新增功能函数 traversal(order, queue)
• 新增遍历方式 BTTraversal::LevelOrder
• 新增公有函数 BTreeNode<T>* thread(BTTraversal order)
• 消除遍历和线索化的代码冗余 ( 代码重构 )

层次遍历算法小结：

1. 将根结点压入队列中
2. 访问队头元素指向的二叉树结点
3. 队头元素弹出，将队头元素的孩子压入队列中
4. 判断队列是否为空 ( 非空：转 2，空：结束 )

层次遍历算法示例：

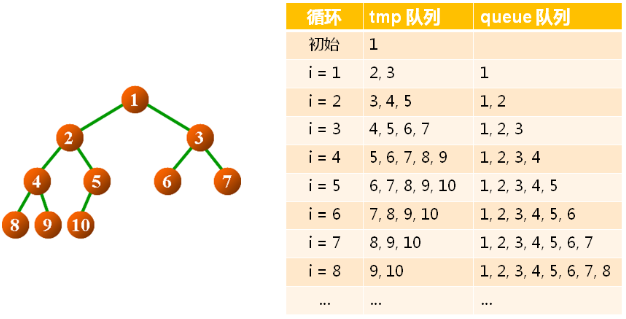
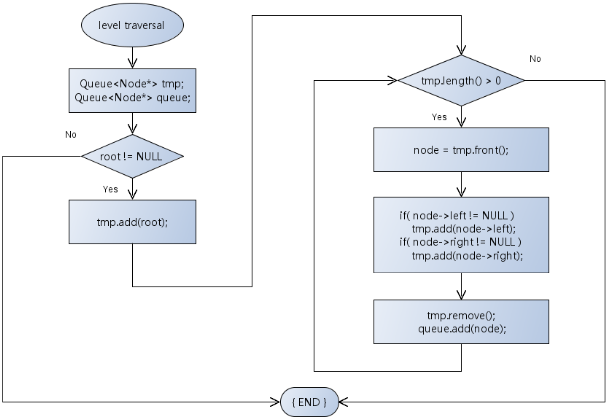
函数接口设计：

• BTreeNode<T>* thread(BTTraversal order)
  1. 根据参数 order 选择线索化的次序 ( 先序，中序，后序，层次 )
  2. 返回值线索化之后指向链表首结点的指针
  3. 线索化执行结束之后对应的二叉树变为空树

线索化流程：

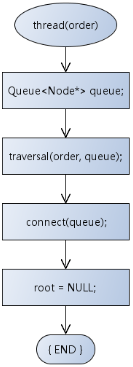
队列中结点的连接算法 [ connect(queue) ]：

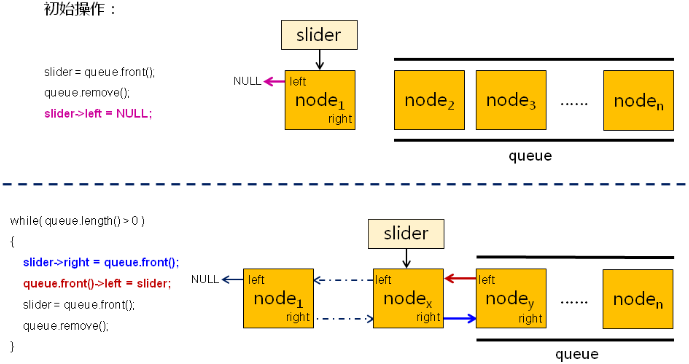
枚举中加入层次遍历：

enum BTTraversal
{
    PreOrder,
    InOrder,
    PostOrder,
    LevelOrder
};

二叉树的线索化：

protected:
    void levelOrderTraversal(BTreeNode<T>* node, LinkQueue<BTreeNode<T>*>& queue) // 层次遍历
    {
        if( node != NULL )
        {
            LinkQueue<BTreeNode<T>*> tmp;

            tmp.add(node);

            while( tmp.length() > 0 )
            {
                BTreeNode<T>* n = tmp.front();

                if( n->left != NULL )
                {
                    tmp.add(n->left);
                }

                if( n->right != NULL )
                {
                    tmp.add(n->right);
                }

                tmp.remove();
                queue.add(n);
            }
        }
    }
    void traversal(BTTraversal order, LinkQueue<BTreeNode<T>*>& queue)
    {
        switch (order)
        {
            case PreOrder:
                preOrderTraversal(root(), queue);
                break;
            case InOrder:
                inOrderTraversal(root(), queue);
                break;
            case PostOrder:
                postOrderTraversal(root(), queue);
                break;
            case LevelOrder:
                levelOrderTraversal(root(), queue);
                break;
            default:
                THROW_EXCEPTION(InvalidParameterException, "Parameter order is invalid ...");
                break;
        }
    }

    BTreeNode<T>* connect(LinkQueue<BTreeNode<T>*>& queue)
    {
        BTreeNode<T>* ret = NULL;

        if( queue.length() > 0 )
        {
            ret = queue.front();

            BTreeNode<T>* slider = queue.front();

            queue.remove();

            slider->left = NULL;

            while( queue.length() > 0 )
            {
                slider->right = queue.front();
                queue.front()->left = slider;
                slider = queue.front();
                queue.remove();
            }

            slider->right = NULL;
        }

        return ret;
    }
public:
    SharedPointer< Array<T> > traversal(BTTraversal order)
    {
        DynamicArray<T>* ret = NULL;
        LinkQueue<BTreeNode<T>*> queue;

        traversal(order, queue);

        ret = new DynamicArray<T>(queue.length());

        if( ret != NULL )
        {
            for(int i=0; i<ret->length(); i++, queue.remove())
            {
                ret->set(i, queue.front()->value);
            }
        }
        else
        {
            THROW_EXCEPTION(NoEnoughMemoryException, "No memory to create return array ...");
        }

        return ret;
    }

    BTreeNode<T>* thread(BTTraversal order)
    {
        BTreeNode<T>* ret = NULL;
        LinkQueue<BTreeNode<T>*> queue;

        traversal(order, queue);

        ret = connect(queue);

        this->m_root = NULL;

        m_queue.clear();

        return ret;
    }

main.cpp测试：

#include <iostream>
#include "BTree.h"

using namespace std;
using namespace StLib;

int main()
{
    BTree<int> bt;
    BTreeNode<int>* n = NULL;

    bt.insert(1, NULL);

    n = bt.find(1);
    bt.insert(2, n);
    bt.insert(3, n);

    n = bt.find(2);
    bt.insert(4, n);
    bt.insert(5, n);

    n = bt.find(4);
    bt.insert(8, n);
    bt.insert(9, n);

    n = bt.find(5);
    bt.insert(10, n);

    n = bt.find(3);
    bt.insert(6, n);
    bt.insert(7, n);

    SharedPointer< Array<int> > tr = bt.traversal(LevelOrder);

    for(int i=0; i<(*tr).length(); i++)
    {
        cout << (*tr)[i] << " ";
    }
    cout << endl;

    BTreeNode<int>* head = bt.thread(LevelOrder);

    while( head != NULL )
    {
        cout << head->value << " ";
        head = head->right;
    }
    cout << endl;

    return 0;
}

运行结果为：

1 2 3 4 5 6 7 8 9 10 
1 2 3 4 5 6 7 8 9 10 

3.二叉树的经典面试题分析

准备代码：

#include <iostream>
#include "BTree.h"

using namespace std;
using namespace StLib;

template < typename T >
BTreeNode<T>* createTree()
{
    static BTreeNode<int> ns[9];

    for(int i=0; i<9; i++)
    {
        ns[i].value = i;
        ns[i].parent = NULL;
        ns[i].left = NULL;
        ns[i].right = NULL;
    }

    ns[0].left = &ns[1];
    ns[0].right = &ns[2];
    ns[1].parent = &ns[0];
    ns[2].parent = &ns[0];

    ns[1].left = &ns[3];
    ns[1].right = NULL;
    ns[3].parent = &ns[1];

    ns[2].left = &ns[4];
    ns[2].right = &ns[5];
    ns[4].parent = &ns[2];
    ns[5].parent = &ns[2];

    ns[3].left = NULL;
    ns[3].right = &ns[6];
    ns[6].parent = &ns[3];

    ns[4].left = &ns[7];
    ns[4].right = NULL;
    ns[7].parent = &ns[4];

    ns[5].left = &ns[8];
    ns[5].right = NULL;
    ns[8].parent = &ns[5];

    return ns;
}

template < typename T >
void printInOrder(BTreeNode<T>* node)
{
    if( node != NULL )
    {
        printInOrder(node->left);

        cout << node->value <<" ";

        printInOrder(node->right);
    }
}

template < typename T >
void printDualList(BTreeNode<T>* node)
{
    BTreeNode<T>* g = node;

    cout << "head -> tail: " << endl;

    while( node != NULL )
    {
        cout << node->value << " ";

        g = node;

        node = node->right;
    }

    cout << endl;

    cout << "tail -> head: " << endl;

    while( g != NULL )
    {
        cout << g->value << " ";

        g = g->left;
    }

    cout << endl;
}

int main()
{
    BTreeNode<int>* ns = createTree<int>();

    printInOrder(ns);
    cout << endl;

    return 0;
}

运行结果为：

3 6 1 0 7 4 2 8 5 

3.1 单度结点删除

面试题一：

• 单度结点删除
  1. 编写一个函数用于删除二叉树中的所有单度结点
  2. 要求：结点删除后，其唯一的子结点替代它的位置

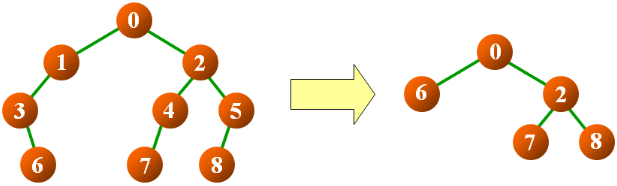
结点中包含指向父结点的指针：

• 定义功能：delOdd1(node)
  1. 删除 node 为根结点的二叉树中的单度结点

单度结点删除（结点中包含指向父结点的指针）：

template < typename T >
BTreeNode<T>* delOdd1(BTreeNode<T>* node)
{
    BTreeNode<T>* ret = NULL;

    if( node != NULL )
    {
        if(((node->left != NULL) && (node->right == NULL)) ||
           ((node->left == NULL) && (node->right != NULL)) )
        {
            BTreeNode<T>* parent = dynamic_cast<BTreeNode<T>*>(node->parent);
            BTreeNode<T>* node_child = (node->left != NULL) ? node->left : node->right;

            if( parent != NULL )
            {
                BTreeNode<T>*& parent_child = (parent->left == node) ? parent->left : parent->right;

                parent_child = node_child;
                node_child->parent = parent;
            }
            else
            {
                node_child->parent = NULL;
            }

            if( node->flag() )
            {
                delete node;
            }

            ret = delOdd1(node_child);
        }
        else
        {
            delOdd1(node->left);
            delOdd1(node->right);

            ret = node;
        }
    }

    return ret;
}

int main()
{
    BTreeNode<int>* ns = createTree<int>();

    printInOrder(ns);
    cout << endl;

    ns = delOdd1(ns);

    printInOrder(ns);
    cout << endl;

    int a[] = {6, 7, 8};
    for(int i=0; i<3; i++)
    {
        TreeNode<int>* n = ns + a[i];

        while( n != NULL )
        {
            cout << n->value << " ";

            n = n->parent;
        }
        cout << endl;
    }

    return 0;
}

运行结果为：

3 6 1 0 7 4 2 8 5 
6 0 7 2 8 
6 0 
7 2 0 
8 2 0 

结点中只包含左右孩子指针：

• 定义功能：delOdd2(node) // node为结点指针的引用
  1. 删除 node 为根结点的二叉树中的单度结点

单度结点删除（结点中只包含左右孩子指针）：

template < typename T >
void delOdd2(BTreeNode<T>*& node)
{
    if( node != NULL )
    {
        if(((node->left != NULL) && (node->right == NULL)) ||
           ((node->left == NULL) && (node->right != NULL)) )
        {
            BTreeNode<T>* node_child = (node->left != NULL) ? node->left : node->right;

            if( node->flag() )
            {
                delete node;
            }

            node = node_child;

            delOdd2(node);
        }
        else
        {
            delOdd2(node->left);
            delOdd2(node->right);
        }
    }
}

int main()
{
    BTreeNode<int>* ns = createTree<int>();

    printInOrder(ns);
    cout << endl;

    delOdd2(ns);

    printInOrder(ns);
    cout << endl;

    return 0;
}

运行结果为：

3 6 1 0 7 4 2 8 5 
6 0 7 2 8 

3.2 中序线索化二叉树

面试题二：

• 中序线索化二叉树
  1. 编写一个函数用于中序线索化二叉树
  2. 要求：不允许使用其它数据结构

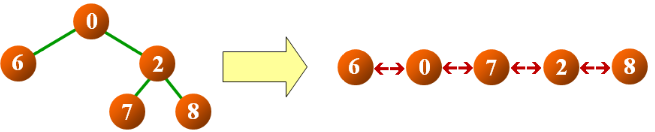
解法一：在中序遍历的同时进行线索化

• 思路：
  1. 使用辅助指针，在中序遍历时指向当前结点的前驱结点
  2. 访问当前结点时，连接与前驱结点的先后次序

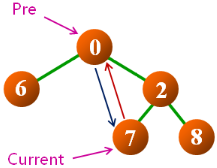
定义功能：inOrderThread(node, pre)

• node：根结点，也是中序访问的结点
• pre：为中序遍历时的前驱结点指针

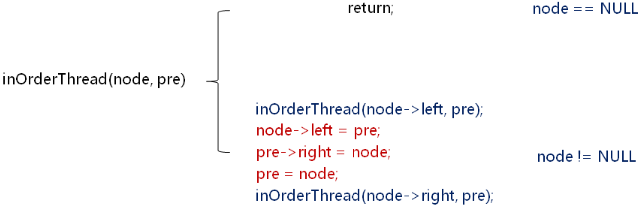
中序线索化二叉树：

template < typename T >
void inOrderThread(BTreeNode<T>* node, BTreeNode<T>*& pre)
{
    if( node != NULL )
    {
        inOrderThread(node->left, pre);

        node->left = pre;

        if( pre != NULL )
        {
            pre->right = node;
        }

        pre = node;

        inOrderThread(node->right, pre);
    }
}

template < typename T >
BTreeNode<T>* inOrderThread1(BTreeNode<T>* node)
{
    BTreeNode<T>* pre = NULL;

    inOrderThread(node, pre);

    while( (node != NULL) && (node->left != NULL) )
    {
        node = node->left;
    }

    return node;
}

int main()
{
    BTreeNode<int>* ns = createTree<int>();

    printInOrder(ns);
    cout << endl;

    delOdd2(ns);

    printInOrder(ns);
    cout << endl;

    ns = inOrderThread1(ns);

    printDualList(ns);

    return 0;
}

运行结果为：

3 6 1 0 7 4 2 8 5 
6 0 7 2 8 
head -> tail: 
6 0 7 2 8 
tail -> head: 
8 2 7 0 6 

解法二：中序遍历的结点次序正好是结点的水平次序

• 思路：
  1. 使用辅助指针，指向转换后双向链表的头结点和尾结点
  2. 根结点与左右子树转换的双向链表连接，成为完整双向链表

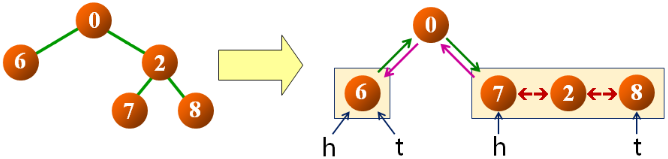
定义功能：inOrderThread(node, head, tail)

• node：根结点，也是中序访问的结点
• head：转换成功后指向双向链表的首结点
• tail：转换成功后指向双链表的尾结点

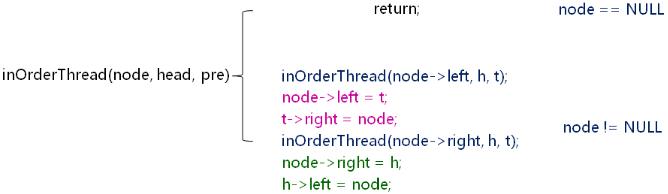
中序线索化二叉树：

template < typename T >
void inOrderThread(BTreeNode<T>* node, BTreeNode<T>*& head, BTreeNode<T>*& tail)
{
    if( node != NULL )
    {
        BTreeNode<T>* h = NULL;
        BTreeNode<T>* t = NULL;

        inOrderThread(node->left, h, t);

        node->left = t;

        if( t != NULL )
        {
            t->right = node;
        }

        head = (h != NULL) ? h : node;

        h = NULL;
        t = NULL;

        inOrderThread(node->right, h, t);

        node->right = h;

        if( h != NULL )
        {
            h->left = node;
        }

        tail = (t != NULL) ? t : node;
    }
}

template < typename T >
BTreeNode<T>* inOrderThread2(BTreeNode<T>* node)
{
    BTreeNode<T>* head = NULL;
    BTreeNode<T>* tail = NULL;

    inOrderThread(node, head, tail);

    return head;
}

int main()
{
    BTreeNode<int>* ns = createTree<int>();

    printInOrder(ns);
    cout << endl;

    ns = inOrderThread2(ns);

    printDualList(ns);

    return 0;
}

运行结果为：

3 6 1 0 7 4 2 8 5 
head -> tail: 
3 6 1 0 7 4 2 8 5 
tail -> head: 
5 8 2 4 7 0 1 6 3 

4.小结

• 比较操作判断两棵二叉树中的数据元素是否对应相等
• 克隆操作将当前二叉树在堆空间中进行复制
• 相加操作将两棵二叉树中的数据元素在对应位置处相加
• 相加操作的结果保存在堆空间的一棵二叉树中

---

• 线索化是将二叉树转换为双向链表的过程
• 线索化之后结点间的先后次序符合某种遍历次序
• 线索化操作将破坏原二叉树结点间的父子关系
• 线索化之后二叉树将不再管理结点的生命期