题目描述
KeineDuck热爱游戏。最近她沉迷于一款名叫“DuckGame”的纸牌。
DuckGame是一款颇有难度的纸牌游戏。在每一轮开始前,会有一些纸牌摆放在玩家的面前,从左到右的第孩堆有ai张纸牌。每张纸牌都是一样的。
游戏开始后,玩家可以选择一个区间[l,r](包括两个端点),并且把这个区中的每一堆纸牌增加或拿走一张纸牌。若每堆纸牌的个数都相同了,玩家即可获胜。我们称这个步骤为一次操作。
KeineDuck想要知道,她至少要进行多少次操作,才能够获胜。
输入
第一行输入一个正整数n,表示有多少堆纸牌。
接下来一行共n个数,第i个数表示第i堆有多少纸牌。
输出
一个整数,表示至少要多少次操作。
样例输入
5
2 1 2 3 3
样例输出
2
提示
样例解释
KeineDuck第一次选择了区间[2,2],将其中的每堆增加了一张纸牌。
KeineDuck第二次选择了区间[4,5],将其中的每堆拿走了一张纸牌。
总共用了2次操作。
对于10%的数据,n=2。
对于另外20%的数据,n=6。
对于另外10%的数据,n=10000,且纸牌的数量从左到右单调递增。
对于另外10%的数据,n=100000,且每堆纸牌的个数不超过2。
对于另外20%的数据,n=100000,且每堆纸牌的个数不超过20。
对于最后30%的数据,n=2000000,且每堆纸牌的个数不超过1000。
比赛完找题解的时候发现在 acwing 上有这道题,然后看各种题解也是发现有小问题,听了yxc大佬的讲解后感觉豁然开朗
附上视频链接:
https://www.acwing.com/problem/content/video/102/
在视频中讲到了四种消除的方法
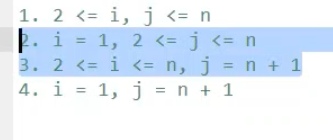
第2,3种方法只能是将一个数消除,第四种方法是无效的方法,没有意义
根据差分的性质,对一个区间进行操作的时候,区间的左端点加上或减去1,而右端点在 r+1上减去或加上 1;贪心一下就是将正数和负数进行匹配消除(第一种方法),(整数减一,负数加一)然后会剩下一些数;这样来说对于剩下的那些数就有两种方法:一个是和一消,一个是和n+1消;就是上面的操作二操作三。
总的次数就是差分数组中正元素的和与abs(负数)的最大值
在这里附上辅助理解的博客:
https://www.cnblogs.com/ZH-comld/p/9673056.html
#include <bits/stdc++.h>
#include <algorithm>
#include <map>
#include <queue>
#include <set>
#include <stack>
#include <string>
#include <vector>
using namespace std;
typedef long long ll;
#define HEAP(...) priority_queue<__VA_ARGS__ >
#define heap(...) priority_queue<__VA_ARGS__,vector<__VA_ARGS__ >,greater<__VA_ARGS__ > >
template<class T> inline T min(T &x,const T &y){return x>y?y:x;}
template<class T> inline T max(T &x,const T &y){return x<y?y:x;}
///#define getchar()(p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
///char buf[(1 << 21) + 1], *p1 = buf, *p2 = buf;
ll read(){ll c = getchar(),Nig = 1,x = 0;while(!isdigit(c) && c!='-')c = getchar();
if(c == '-')Nig = -1,c = getchar();
while(isdigit(c))x = ((x<<1) + (x<<3)) + (c^'0'),c = getchar();
return Nig*x;}
#define read read()
const ll inf = 1e15;
const ll INF = 0x3f3f3f3f;
const int maxn = 2e6 + 7;
const int mod = 1e9 + 7;
#define end return 0
ll maxx=-1;
ll minn=inf;
ll num[maxn];
ll a[maxn];
ll num2[maxn];
ll res,ans;
map<ll,ll> mp;
priority_queue <int ,vector<int> ,greater<int> > xiaogen;
bool cmp(ll a,ll b){
return a>b;
}
ll chafen[maxn];
int main()
{
int n=read;
for(int i=1;i<=n;i++) num[i]=read;
for(int i=2;i<=n;i++){
ll temp=num[i]-num[i-1];
if(temp>0) ans+=temp;
else res-=temp;
}
cout<<max(ans,res)<<endl;
return 0;
}
/**************************************************************
Problem: 15270
Language: C++
Result: 正确
Time:136 ms
Memory:64528 kb
****************************************************************/