动态规划解决机器人网格路径问题！

想获得更好的排版，请移步个人博客： https://pushy.site

无障碍物

题目（原题见 LeetCode - 62. 不同路径）：一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。问总共有多少条不同的路径？

示例 1:

输入: m = 3, n = 2
输出: 3
解释:
从左上角开始，总共有 3 条路径可以到达右下角。

1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右

通过观察我们我们得出以下两个特点：

1. 机器人所在的正东方向和正南方向，只能有一条路径可以走，即直走。
2. 到某个点的路径 = 到该点上一个单位的点路径 + 到该点左一个单位的点路径。

为了验证第二个特点，我们假设网格是 2 * 2。如下图所示，从 A 到达 D 点的路径总和就等于 A 点到达 B 点的路径 + 到达 C 点的路径总和。

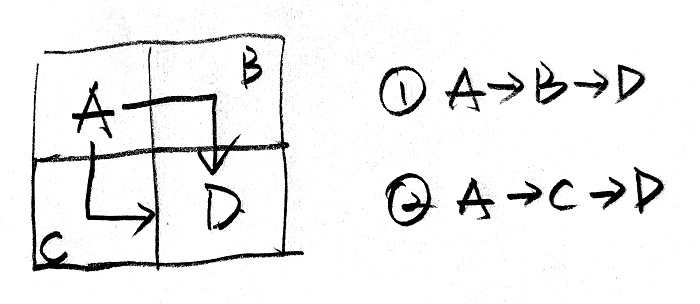
这样，我们不难写出递归代码：

public int solution(int m, int n) {
    if (m <= 0 || n <= 0)
        return 0;
    else if (m == 1 || n == 1)
        return 1;
    
    int result = 0;
    result += rec(m - 1, n);
    result += rec(m, n - 1);
    return result;
}

递归代码虽然简单，但是和斐波那契数列递归实现一样，会出现重复子树的情况。例如求 4 * 3 的路径时，就出现了递归计算重复子树的情况：

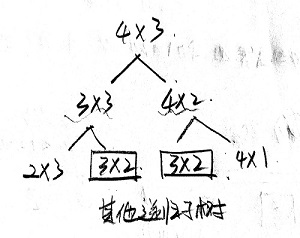
和斐波那契一样，可以用动态规划来优化复杂度，不难写出状态转移方程为：f(i, j) = f(i - 1)(j) + f(i)(j - 1)

public int solution(int m, int n) {
    int[][] dp = new int[n][m];

    for (int i = 0; i < n; i++) { // 第一列
        dp[i][0] = 1;
    }
    for (int i = 0; i < m; i++) { // 第一行
        dp[0][i] = 1;
    }
    for (int i = 1; i < n; i++) {
        for (int j = 1; j < m; j++) {
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        }
    }
    return dp[n - 1][m - 1];
}

有障碍物

现在，保持和无障碍物的题意，在网格中设置了障碍物（机器人无法越过障碍物），求到终点的路径总和。原题见 LeetCode - 63. 不同路径 II

虽然增加了障碍物，但是前面总结的两个特点还是适用的。但是，需要做一些改变：

• 对于正东和正南的方向路径，一旦遇到障碍物（1），代表无法通过，则后面的路径全是 0；
• 第二个特点仅使用于该点不是障碍物；如果为障碍物，则直接将该点路径设为 0，代表从该点无法通过。

LeetCode 官方图解如下：

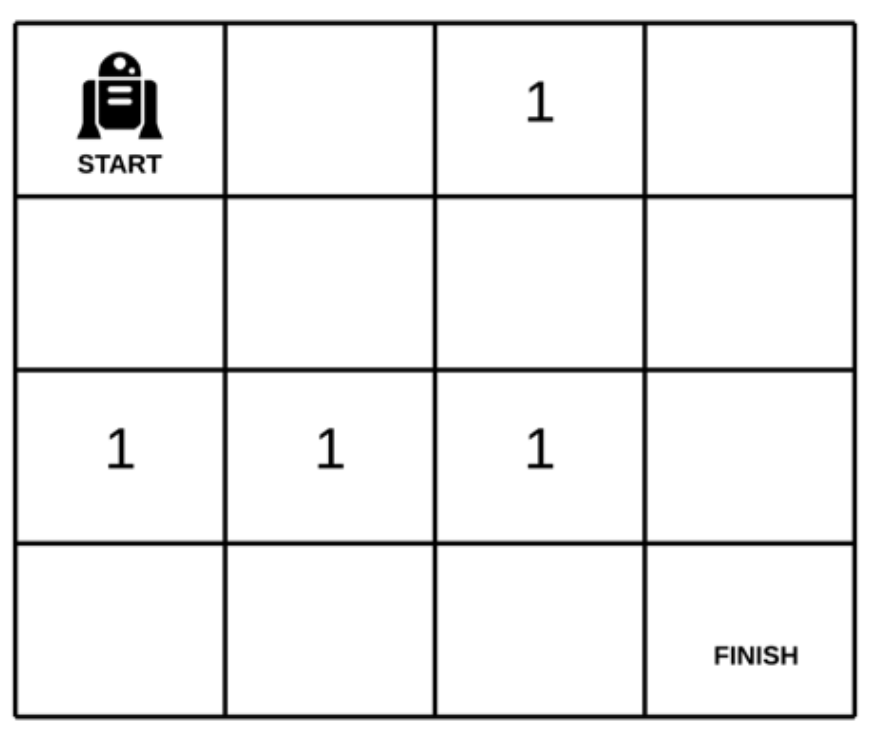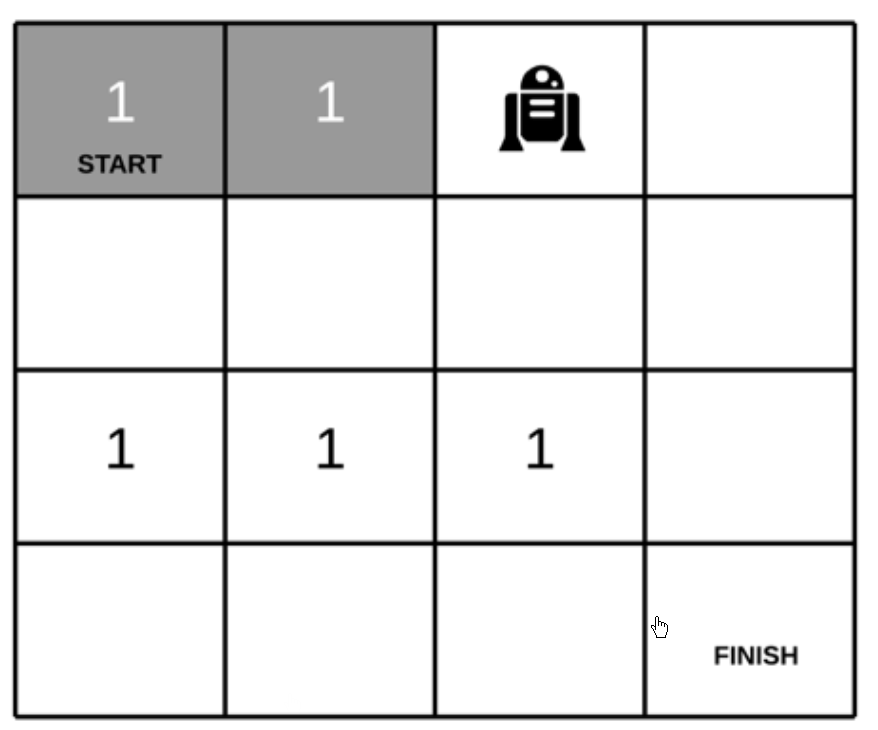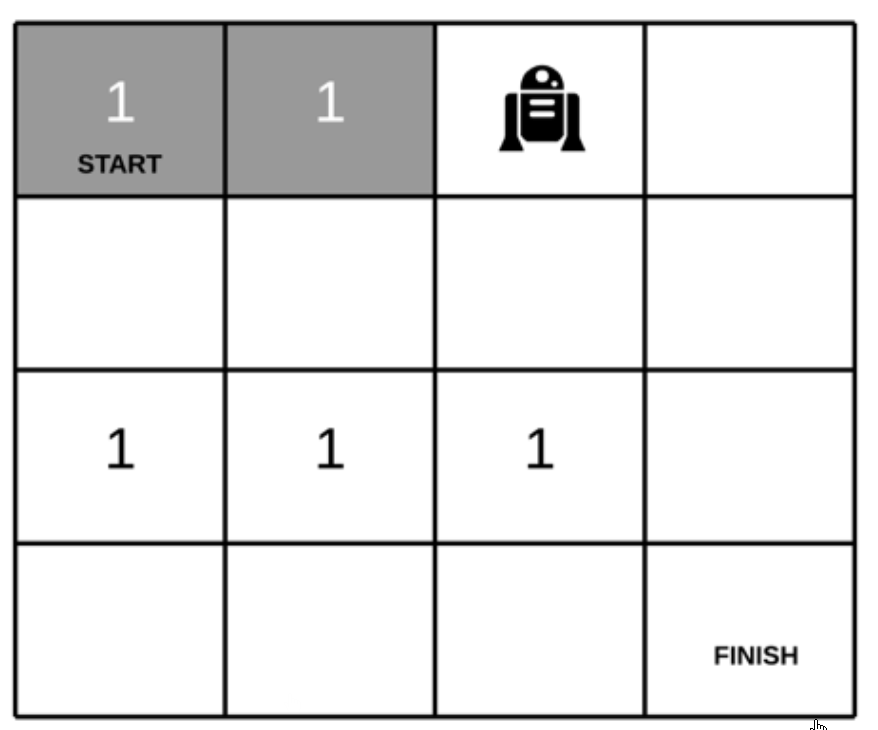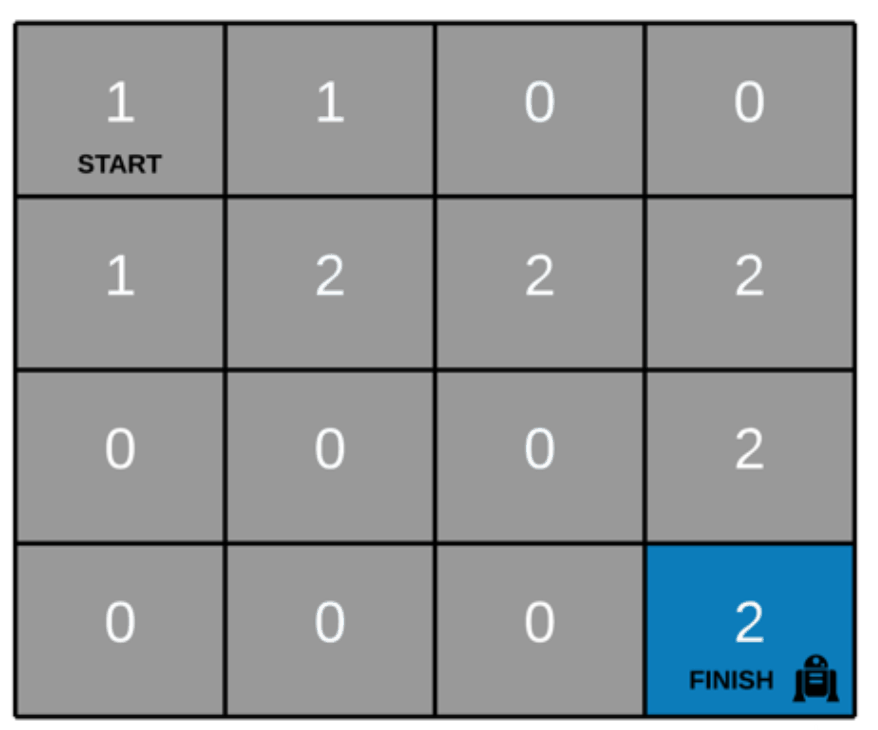
public int uniquePathsWithObstacles(int[][] matrix) {
    if (matrix == null) return 0;

    int n = matrix.length;
    int m = matrix[0].length;

    int[][] dp = new int[n][m];
    dp[0][0] = matrix[0][0] == 0 ? 1 : 0;
    if (dp[0][0] == 0) {
        return 0;
    }

    // 第一列
    for (int i = 1; i < n; i++) {
        if (matrix[i][0] != 1) {
            dp[i][0] = dp[i - 1][0];
        }
    }
    // 第一行
    for (int j = 1; j < m; j++) {
        if (matrix[0][j] != 1) {
            dp[0][j] = dp[0][j - 1];
        }
    }

    for (int i = 1; i < n; i++) {
        for (int j = 1; j < m; j++) {
            if (matrix[i][j] != 1) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
    }
    return dp[n - 1][m - 1];
}