我们知道,n代表的是table的长度length,之前一再强调,表table的长度需要取2的整数次幂,就是为了这里等价这里进行取模运算时的方便——取模运算转化成位运算公式:a%(2^n) 等价于 a&(2^n-1),而&操作比%操作具有更高的效率。
当length=2n时,(length - 1)正好相当于一个"低位掩码","与"操作的结果就是散列值的高位全部归零,只保留低位,用来做数组下标访问:

可以看到,当我们的length为16的时候,哈希码(字符串“abcabcabcabcabc”的key对应的哈希码)对(16-1)与操作,对于多个key生成的hashCode,只要哈希码的后4位为0,不论不论高位怎么变化,最终的结果均为0。也就是说,如果支取后四位(低位)的话,这个时候产生"碰撞"的几率就非常大(当然&运算中产生碰撞的原因很多,这里只是举个例子)。为了解决低位与操作碰撞的问题,于是便有了第二步中高16位异或低16位的“扰动函数”。
右移16位,自己的高半区和低半区异或,就是为了混合原始哈希码的高位和低位,以此来加大低位随机性。
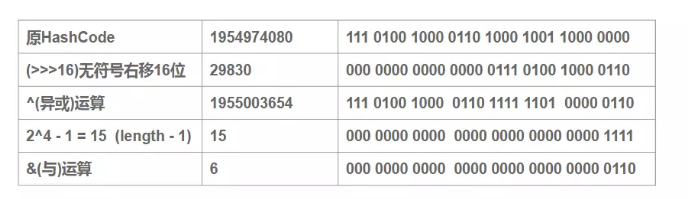
可以看到: 扰动函数优化前:1954974080 % 16 = 1954974080 & (16 - 1) = 0 扰动函数优化后:1955003654 % 16 = 1955003654 & (16 - 1) = 6 很显然,减少了碰撞的几率。