第1讲 第1部分 层次分析法模型讲解
数学建模三大块:建模+编程+写作
模型讲解
从简单的例子开始,慢慢的引出模型。(体验真正的建模过程)
编程讲解
不需要MATLAB基础,先讲基础语法和函数,再讲模型的实现(注释详细)。
写作训练
每一讲结束后都会有相应的作业供你练习。
每个算法都会配有拓展资料。(看看优秀论文是如何写作的吧)
第一讲:层级分析法
(The analytic hierarchy process,简称AHP)
建模比赛中最基础的模型之一。其主要用于解决评价类问题(例如:选择哪种方案最好、哪位运动员或者员工表现得更优秀)。
评价类问题可用打分解决

小明最关心大学里面的这四个方面:
学习氛围(\(0.4\))
就业前景(\(0.3\))
男女比例(\(0.2\))
校园景色(\(0.1\))
括号里面的数值表示小明认为的重要性程度(权重),其和为\(1\)。
注:本例子仅用于学习,大家可暂时忽略真实情况下应考虑到的更多细节(例如学校中的具体专业)。


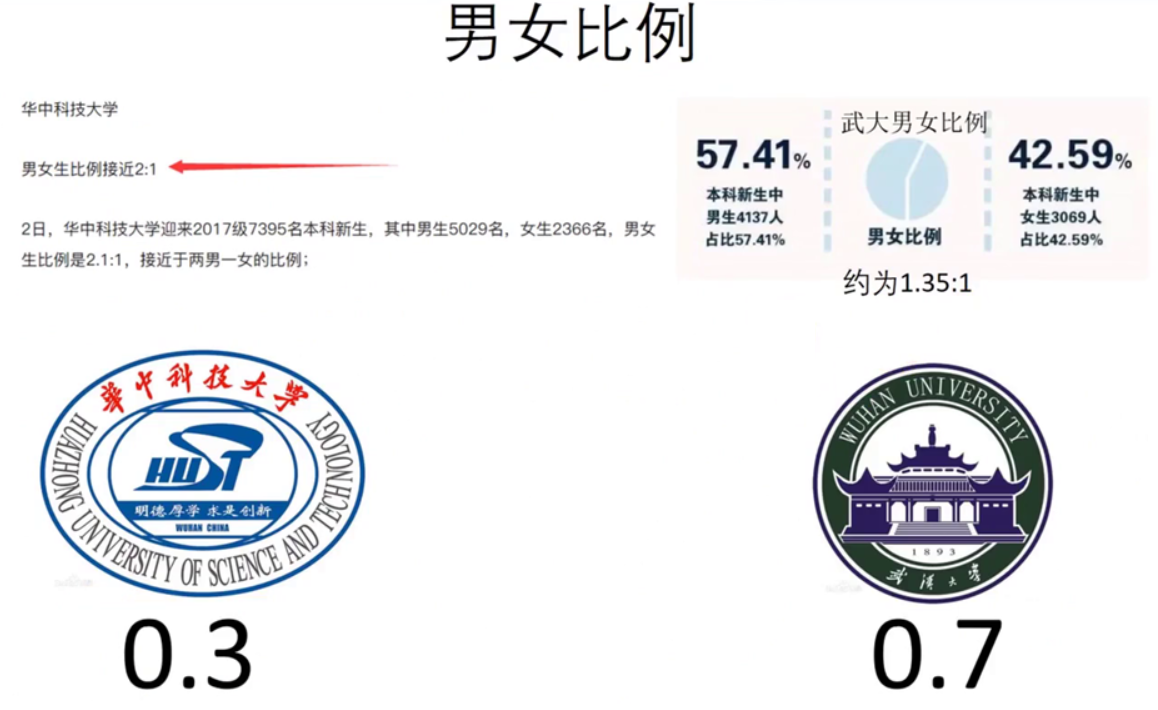

小明整理好了这张权重表格:
| 指标权重 | 华科 | 武大 | |
|---|---|---|---|
| 学习氛围 | \(0.4\) | \(\color{CornflowerBlue}{0.7}\) | \(\color{OrangeRed}{0.3}\) |
| 就业前景 | \(0.3\) | \(\color{CornflowerBlue}{0.5}\) | \(\color{OrangeRed}{0.5}\) |
| 男女比例 | \(0.2\) | \(\color{CornflowerBlue}{0.3}\) | \(\color{OrangeRed}{0.7}\) |
| 校园景色 | \(0.1\) | \(\color{CornflowerBlue}{0.25}\) | \(\color{OrangeRed}{0.75}\) |
华科最终得分:\(0.515\)
武大最终得分:\(0.485\)
由于华科分数高于武大,小明最终选择了华科。。。
一个小小的总结
用打分法解决评价问题,只需要我们补充完成下面这张表格即可:
| 指标权重 | 方案1 | 方案2 | \(\cdots\) | |
|---|---|---|---|---|
| 指标1 | \(\color{RoyalBlue}{1}\) | \(\color{Salmon}{2}\) | \(\color{Salmon}{2}\) | \(\color{Salmon}{2}\) |
| 指标2 | \(\color{RoyalBlue}{1}\) | \(\color{YellowGreen}{3}\) | \(\color{YellowGreen}{3}\) | \(\color{YellowGreen}{3}\) |
| 指标3 | \(\color{RoyalBlue}{1}\) | \(\color{DarkOrchid}{4}\) | \(\color{DarkOrchid}{4}\) | \(\color{DarkOrchid}{4}\) |
| \(\cdots\) | \(\color{RoyalBlue}{1}\) | \(\color{Brown}{5}\) | \(\color{Brown}{5}\) | \(\color{Brown}{5}\) |
同颜色数字的单元格的和为\(1\),它们表示的针对某一因素所占的权重。
一道引出层次分析法的例题
填好志愿后,小明同学想出去旅游。在查阅了网上的攻略后,他初步选择了苏杭、北戴河和桂林三地之一作为目标景点。
请你确定评价指标、形成评价体系来为小明同学选择最佳的方案。
评价类问题
解决评价类问题,大家首先要想到以下三个问题:
① 我们评价的目标是什么?
答:为小明同学选择最佳的旅游景点。
② 我们为了达到这个目标有哪几种可选的方案?
答:三种,分别是去苏杭、去北戴河和去桂林
③ 评价的准则或者说指标是什么?(我们根据什么东西来评价好坏)
答:题目没给相关数据支撑,需要我们查阅相关的资料。
一般而言,前两个问题的答案是显而易见的,第三个问题的答案需要我们根据题目中的背景材料、常识以及网上搜集到的参考资料进行结合,从中筛选出最合适的指标。
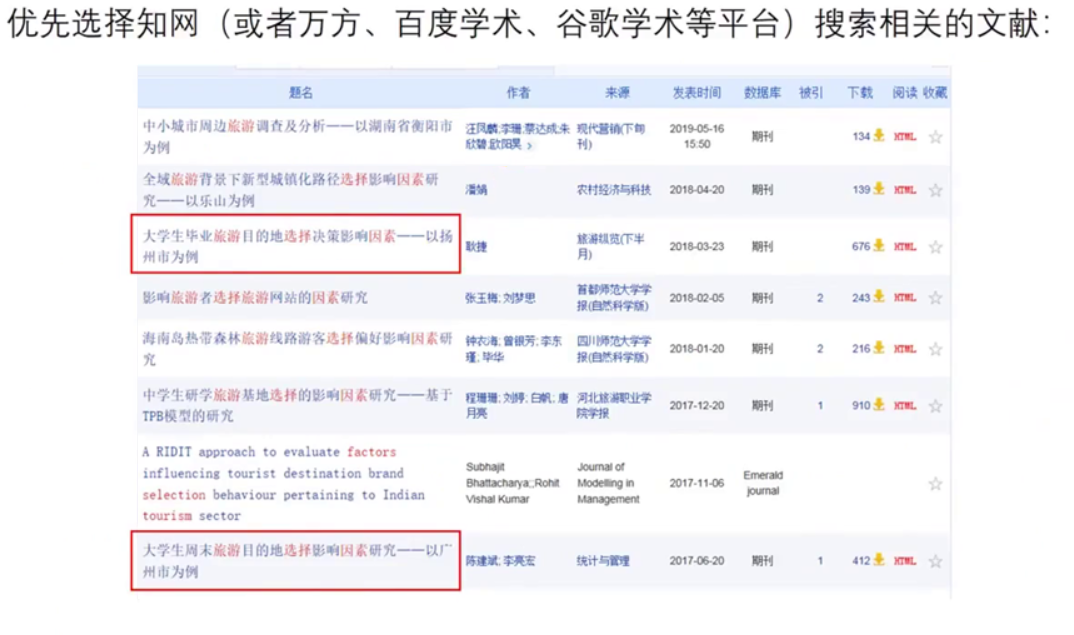
为什么优先再别人发表的论文中寻找指标?
显得专业
另外,别人研究使用的方法你也可以借鉴
假如你没有找到相关文献怎么办?
和小组成员来场头脑风暴+在平台上搜索别人或者专家的看法呗
强烈推荐一个很腻害的网站:
虫部落-快搜
优先级
- 谷歌搜索(国内进不去的话就使用百度搜索吧)
- 微信搜索
- 知乎搜索
例如本题我们可以搜索关键字:
旅游选择因素、根据什么因素选择旅游景点、旅游景点评价指标等
假如我们查询了资料后选择了以下五个指标
① 景点景色
② 旅游花费
③ 居住环境
④ 饮食情况
⑤ 交通便利程度
脑洞:假如现在小明就在我们面前,我们要对他提哪些问题才能帮他合理地做决定?
还记得这张权重表格吗?
| 指标权重 | 苏杭 | 北戴河 | 桂林 | |
|---|---|---|---|---|
| 景色 | \(\color{RoyalBlue}{1}\) | \(\color{Salmon}{2}\) | \(\color{Salmon}{2}\) | \(\color{Salmon}{2}\) |
| 花费 | \(\color{RoyalBlue}{1}\) | \(\color{YellowGreen}{3}\) | \(\color{YellowGreen}{3}\) | \(\color{YellowGreen}{3}\) |
| 居住 | \(\color{RoyalBlue}{1}\) | \(\color{DarkOrchid}{4}\) | \(\color{DarkOrchid}{4}\) | \(\color{DarkOrchid}{4}\) |
| 饮食 | \(\color{RoyalBlue}{1}\) | \(\color{Brown}{5}\) | \(\color{Brown}{5}\) | \(\color{Brown}{5}\) |
| 交通 | \(\color{RoyalBlue}{1}\) | \(\color{Tan}{6}\) | \(\color{Tan}{6}\) | \(\color{Tan}{6}\) |
有同学可能会想,直接叫小明填好这张表不就完事啦~
这样往往比较片面和不周全(隔一天问他答案可能就变了)
在确定影响某因素的诸因子在该因素中所占的比重时,遇到的主要困难是这些比重常常不易定量化。此外,当影响某因素的因子较多时,直接考虑各因子对该因素有多大程度的影响时,常常会因考虑不周全、顾此失彼而使决策者提出与他实际认为的重要性程度不相一致的数据,甚至有可能提出一组隐含矛盾的数据。
——选自司守奎老师的《数学建模算法与应用教材》
分而治之的思想
分而治之:我们先来确定指标的权重吧~
问题:一次性考虑这五个指标之间的关系,往往考虑不周。
解决方法:两个两个指标进行比较,最终根据两两比较的结果来推算出权重。
层次分析法的思想登场
如果用\(1-9\)表示重要程度(见下表),请你两两比较上述这五个指标对于选择最终的旅游景点的重要性。
| 标度 | 含义 |
|---|---|
| \(1\) | 表示两个因素相比,具有相同重要性 |
| \(3\) | 表示两个因素相比,一个因素比另一个因素稍微重要 |
| \(5\) | 表示两个因素相比,一个因素比另一个因素明显重要 |
| \(7\) | 表示两个因素相比,一个因素比另一个因素强烈重要 |
| \(9\) | 表示两个因素相比,一个因素比另一个因素极端重要 |
| \(2,4,6,8\) | 上述两相邻判断的中值 |
| 倒数 | A和B相比如果标度为\(3\),那么B和A相比就是\(\frac{1}{3}\) |
注:这里的重要性有时候解释为满意度更方便理解
| 景色 | 花费 | 居住 | 饮食 | 交通 | |
|---|---|---|---|---|---|
| 景色 | \(1\) | \(\color{OrangeRed}{\frac{1}{2}}\) | \(\color{RoyalBlue}{4}\) | \(3\) | \(3\) |
| 花费 | \(\color{OrangeRed}{2}\) | \(1\) | \(7\) | \(5\) | \(5\) |
| 居住 | \(\color{RoyalBlue}{\frac{1}{4}}\) | \(\frac{1}{7}\) | \(1\) | \(\frac{1}{2}\) | \(\frac{1}{3}\) |
| 饮食 | \(\frac{1}{3}\) | \(\frac{1}{5}\) | \(2\) | \(1\) | \(1\) |
| 交通 | \(\frac{1}{3}\) | \(\frac{1}{5}\) | \(3\) | \(1\) | \(1\) |
\(\color{OrangeRed}{Q1}\):根据上面这个表,请你比较景色和花费的重要程度。
\(\color{OrangeRed}{A1}\):我认为花费比景色略微重要(介于同等重要\(1\)和稍微重要\(3\)之间吧)
\(\color{RoyalBlue}{Q2}\):根据上面这个表,请你比较景色和居住的重要程度。
\(\color{RoyalBlue}{A1}\):我认为景色比居住要重要一点(介于稍微重要\(3\)和明显重要\(5\)之间吧)
就这样,小明回答了\(10\)次(组合数\(C_5^2\)),你根据他所回答的填好了上面这张表。
注:实际情况下没有小明帮我们回答,层级分析法种这张表是交给“专家”填的,具体我们等后面再说。
总结:上面这个表是一个\(5 \times 5\)的方阵,我们记为\(A\),对应的元素为\(a_{ij}\)。
这个方阵有如下特点:
(1)\(a_{ij}\)表示的意义是,与指标\(j\)相比,\(i\)的重要程度。
(2) 当\(i=j\)时,两个指标相同,因此同等重要记为\(1\),这就解释了主对角线元素为\(1\)。
(3) \(a_{ij}>0\)且满足\(a_{ij} \times a_{ji}=1\)(我们称满足这一条件的矩阵为正互反矩阵)
实际上,上面这个矩阵就是层次分析法中的判断矩阵。
得到了判断矩阵,就可以计算出权重了。具体方法我们稍后再讲。
如何计算苏杭、北戴河与桂林在景色方面所占的权重(得分)呢?
填写判断矩阵
| 景色 | 苏杭 | 北戴河 | 桂林 |
|---|---|---|---|
| 苏杭 | \(1\) | \(2\) | \(5\) |
| 北戴河 | \(\frac{1}{2}\) | \(1\) | \(2\) |
| 桂林 | \(\frac{1}{5}\) | \(\frac{1}{2}\) | \(1\) |
Q1:你觉得苏杭的风景和北戴河相比如何?
A1:稍微好一点点吧(介于\(1-3\)之间)
Q2:你觉得苏杭的风景和桂林相比如何?
A2:要明显的好哦(\(5\))
Q3:你觉得北戴河的风景和桂林相比如何?
A3:稍微好一点点吧(介于\(1-3\)之间)
| 花费 | 苏杭 | 北戴河 | 桂林 |
|---|---|---|---|
| 苏杭 | \(1\) | \(\frac{1}{3}\) | \(\frac{1}{8}\) |
| 北戴河 | \(3\) | \(1\) | \(\frac{1}{3}\) |
| 桂林 | \(8\) | \(3\) | \(1\) |
| 居住 | 苏杭 | 北戴河 | 桂林 |
|---|---|---|---|
| 苏杭 | \(1\) | \(1\) | \(3\) |
| 北戴河 | \(1\) | \(1\) | \(3\) |
| 桂林 | \(\frac{1}{3}\) | \(\frac{1}{3}\) | \(1\) |
| 饮食 | 苏杭 | 北戴河 | 桂林 |
|---|---|---|---|
| 苏杭 | \(1\) | \(3\) | \(4\) |
| 北戴河 | \(\frac{1}{3}\) | \(1\) | \(1\) |
| 桂林 | \(\frac{1}{4}\) | \(1\) | \(1\) |
| 交通 | 苏杭 | 北戴河 | 桂林 |
|---|---|---|---|
| 苏杭 | \(1\) | \(1\) | \(\frac{1}{4}\) |
| 北戴河 | \(1\) | \(1\) | \(\frac{1}{4}\) |
| 桂林 | \(4\) | \(4\) | \(1\) |
一个有可能出问题的地方
苏杭\(=A\),北戴河\(=B\),桂林\(=C\)
苏杭比北戴河景色好一点\(A>B\)
苏杭和桂林景色一样好\(A=C\)
北戴河比桂林景色好一点\(B>C\)
| 景色 | 苏杭 | 北戴河 | 桂林 |
|---|---|---|---|
| 苏杭 | \(1\) | \(2\) | \(\color{Red}{1}\) |
| 北戴河 | \(\frac{1}{2}\) | \(1\) | \(2\) |
| 桂林 | \(\color{Red}{1}\) | \(\frac{1}{2}\) | \(1\) |
出现了矛盾之处(不一致的现象)
要是把上表中的\(2\)换成更大的数,那么不一致会更加严重
一致矩阵
\(a_{ij}=\frac{i的重要程度}{j的重要程度},\;a_{jk}=\frac{j的重要程度}{k的重要程度}\)
\(a_{ik}=\frac{i的重要程度}{k的重要程度}=a_{ij} \times a_{jk}\)
一致矩阵的例子
| 景色 | 苏杭 | 北戴河 | 桂林 |
|---|---|---|---|
| 苏杭 | \(1\) | \(2\) | \(4\) |
| 北戴河 | \(\frac{1}{2}\) | \(1\) | \(2\) |
| 桂林 | \(\frac{1}{4}\) | \(\frac{1}{2}\) | \(1\) |
| 景色 | 花费 | 居住 | 饮食 | 交通 | |
|---|---|---|---|---|---|
| 景色 | \(1\) | \(\frac{1}{2}\) | \(4\) | \(3\) | \(3\) |
| 花费 | \(2\) | \(1\) | \(8\) | \(6\) | \(6\) |
| 居住 | \(\frac{1}{4}\) | \(\frac{1}{8}\) | \(1\) | \(\frac{3}{4}\) | \(\frac{3}{4}\) |
| 饮食 | \(\frac{1}{3}\) | \(\frac{1}{6}\) | \(\frac{4}{3}\) | \(1\) | \(1\) |
| 交通 | \(\frac{1}{3}\) | \(\frac{1}{6}\) | \(\frac{4}{3}\) | \(1\) | \(1\) |
观察上面这两个矩阵的特点:各行(各列)之间成倍数关系
【一致矩阵的定义】
若矩阵中每个元素\(a_{ij}>0\)且满足\(a_{ij} \times a_{jk}=1\),则我们称该矩阵为正互反矩阵。
在层次分析法中,我们构造的判断矩阵均是正互反矩阵。
若正互反矩阵满足\(a_{ij} \times a_{jk}=a_{ik}\),则我们称其为一致矩阵。
注意:在使用判断矩阵求权重之前,必须对其进行一致性检验。
一致性检验
【原理】:检验我们构造的判断矩阵和一致矩阵是否有太大的差别。
下面的知识需要用到线性代数的知识,没学过的同学可以忽略掉证明过程,只需要了解如何计算即可。
\(\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix}\)为一致矩阵的充要条件:\(\begin{cases} a_{ij}>0 \\a_{11}=a_{22}=\cdots=a_{nn}=1\\ [a_{i1},a_{i2},\cdots,a_{in}]=k_i[a_{11},a_{12},\cdots,a_{1n}] \end{cases}\)
引理:\(A\)为\(n\)阶方阵,且\(r(A)=1\),则\(A\)有一个特征值为\(tr(A)\),其余特征值均为\(0\)。
因为一致矩阵的各行成比例,所以一致矩阵的秩一定为\(1\)。
由引理可知:一致矩阵有一个特征值为\(n\),其余特征值均为\(0\)。
另外,我们很容易得到,特征值为\(n\)时,对应的特征向量刚好为\(k[\frac{1}{a_{11}},\frac{1}{a_{12}},\cdots,\frac{1}{a_{1n}}]^T(k \not= 0)\)
计算可看:EIG_consistent_matrix.m(提取码:ncst)
若正互反矩阵满足\(a_{ij} \times a_{jk}=a_{ik}\),则我们称其为一致矩阵。
引理:\(n\)阶正互反矩阵\(A\)为一致矩阵时当且仅当最大特征值\(\lambda_{max}=n\)。
且当正互反矩阵\(A\)非一致时,一定满足\(\lambda_{max}>n\)。

判断矩阵越不一致时,最大特征值与\(n\)相差就越大。
代码文件名称:PPT_1.m(提取码:ncst)
一致性检验的步骤
第一步:计算一致性指标\(CI\)
第二步:查找对应的平均随机一致性指标\(RI\)
| \(n\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) | \(8\) | \(9\) | \(10\) | \(11\) | \(12\) | \(13\) | \(14\) | \(15\) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(RI\) | \(0\) | \(0\) | \(0.52\) | \(0.89\) | \(1.12\) | \(1.26\) | \(1.36\) | \(1.41\) | \(1.46\) | \(1.49\) | \(1.52\) | \(1.54\) | \(1.56\) | \(1.58\) | \(1.59\) |
注:在实际运用中,\(n\)很少超过\(10\),如果指标的个数大于\(10\),则可考虑建立二级指标体系
第三步:计算一致性比例\(CR\)
如果\(CR<0.1\),则可认为判断矩阵的一致性可以接收;否则需要对判断矩阵进行修正。
两个小问题
一致性指标\(CI=\frac{\lambda_{max}-n}{n-1}\),一致性比例\(CR=\frac{CI}{RI}\begin{cases}<0.1,判断矩阵一致\\\geqslant0.1,判断矩阵不一致\end{cases}\)
(1)平均随机一致性指标\(RI\)怎么计算来的?
\(RI\)的值是这样得到的,用随机方法构造\(500\)个样本矩阵:随机地从\(1 \sim 9\)及其倒数中抽取数字构造正互反矩阵,求得最大特征根的平均值\(\lambda'_{max}\),并定义
\[RI=\frac{\lambda'_{max}-n}{n-1} \]
(2)为什么要这样构造\(CI\),为什么要以\(0.1\)为划分依据?
大家有兴趣的话可以去查看作者的原论文,作者是通过多次蒙特卡罗模拟得到的最佳的方案。
一致矩阵怎么计算权重?
从最简单的开始入手,先来看一致矩阵:
| 景色 | 苏杭 | 北戴河 | 桂林 |
|---|---|---|---|
| 苏杭 | \(1\) | \(2\) | \(4\) |
| 北戴河 | \(\frac{1}{2}\) | \(1\) | \(2\) |
| 桂林 | \(\frac{1}{4}\) | \(\frac{1}{2}\) | \(1\) |
对于景色这点而言:
注:这里的重要性有时候解释为满意度更方便理解)
苏杭的重要性如果是\(1\),那么北戴河的重要性就是\(\frac{1}{2}\),桂林的重要性就是\(\frac{1}{4}\).
注意:权重一定要进行归一化处理:
判断矩阵计算权重
| 景色 | 苏杭 | 北戴河 | 桂林 |
|---|---|---|---|
| 苏杭 | \(1\) | \(2\) | \(5\) |
| 北戴河 | \(\frac{1}{2}\) | \(1\) | \(2\) |
| 桂林 | \(\frac{1}{5}\) | \(\frac{1}{2}\) | \(1\) |
仅使用第一列的数据,计算出来的权重:
使用第二列的数据,计算出来的权重:
使用第三列的数据,计算出来的权重:
综合上述三列,我们求平均权重:
方法1:算术平均法求权重
第一步:将判断矩阵按照列归一化(每一个元素除以其所在列的和)
| 景色 | 苏杭 | 北戴河 | 桂林 |
|---|---|---|---|
| 苏杭 | \(0.5882\) | \(0.5714\) | \(0.625\) |
| 北戴河 | \(0.2941\) | \(0.2857\) | \(0.25\) |
| 桂林 | \(0.1177\) | \(0.1429\) | \(0.125\) |
第二步:将归一化的各列相加(按行求和)
| 未归一化的权重 | |
|---|---|
| 苏杭 | \(0.5882+0.5714+0.625=1.7846\) |
| 北戴河 | \(0.2941+0.2857+0.25=0.8298\) |
| 桂林 | \(0.1177+0.1429+0.125=0.3856\) |
第三步:将相加后得到的向量中每个元素除以\(n\)即可得到权重向量
| 权重 | |
|---|---|
| 苏杭 | \(\frac{1.7846}{3}=0.5949\) |
| 北戴河 | \(\frac{0.8298}{3}=0.2766\) |
| 桂林 | \(\frac{0.3856}{3}=0.1285\) |
假设判断矩阵\(A=\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix}\),
那么算术平均法求得得权重向量\(\omega_i=\frac{1}{n}\sum_{j=1}^{n}\frac{a_{ij}}{\sum_{k=1}^n a_{kj}},(i=1,2,\cdots,n)\)
方法2:几何平均法求权重
几何平均法求权重也有三步:
第一步:将\(A\)的元素按照行相乘得到一个新的列向量
第二步:将新的向量的每个分量开\(n\)次方
第三步:对该列向量进行归一化即可得到权重向量
假设判断矩阵\(A=\begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix}\),
那么算术平均法求得得权重向量\(\omega_i=\frac{(\Pi_{j=1}^n a_{ij})^{\frac{1}{n}}}{\sum_{k=1}^{n}(\Pi_{j=1}^{n} a_{kj})^{\frac{1}{n}}},(i=1,2,\cdots,n)\)
| 算术平均法权重 | 几何平均法权重 | |
|---|---|---|
| 苏杭 | \(0.5949\) | \(0.5954\) |
| 北戴河 | \(0.2766\) | \(0.2764\) |
| 桂林 | \(0.1285\) | \(0.1283\) |
注:权重和应为\(1\),这里由于四舍五入所以会有可以忽略的差距。
方法3:特征值法求权重
一致矩阵有一个特征值为\(n\),其余特征值均为\(0\)。
另外,我们很容易得到,特征值为\(n\)时,对应的特征向量刚好为\(k[\frac{1}{a_{11}},\frac{1}{a_{12}},\cdots,\frac{1}{a_{1n}}]^T(k \not= 0)\)
这一特征向量刚好就是一致矩阵的第一列。
| 景色 | 苏杭 | 北戴河 | 桂林 |
|---|---|---|---|
| 苏杭 | \(\color{OrangeRed}{1}\) | \(2\) | \(4\) |
| 北戴河 | \(\color{OrangeRed}{\frac{1}{2}}\) | \(1\) | \(2\) |
| 桂林 | \(\color{OrangeRed}{\frac{1}{4}}\) | \(\frac{1}{2}\) | \(1\) |
注意:权重一定要进行归一化处理:
假如我们的判断矩阵一致性可以接受,那么我们可以仿照一致矩阵权重的求法。
第一步:求出矩阵\(A\)的最大特征值以及其对应的特征向量
第二步:对求出的特征向量进行归一化即可得到我们的权重
| 景色 | 苏杭 | 北戴河 | 桂林 |
|---|---|---|---|
| 苏杭 | \(1\) | \(2\) | \(\color{OrangeRed}{5}\) |
| 北戴河 | \(\frac{1}{2}\) | \(1\) | \(2\) |
| 桂林 | \(\color{OrangeRed}{\frac{1}{5}}\) | \(\frac{1}{2}\) | \(1\) |
最大特征值为\(3.0055\),一致性比例\(CR=0.0053\)
对应的特征向量:\([-0.8902,\;-0.4132,\;-0.1918]\)
对其归一化:\([0.5954,\;0.2764,\;0.1283]\)
| 算术平均法 | 几何平均法 | 特征值法 | |
|---|---|---|---|
| 苏杭 | \(0.5949\) | \(0.5954\) | \(\color{Salmon}{0.5954}\) |
| 北戴河 | \(0.2766\) | \(0.2764\) | \(\color{Salmon}{0.2764}\) |
| 桂林 | \(0.1285\) | \(0.1283\) | \(\color{Salmon}{0.1283}\) |
将计算结果填入权重表
| 指标权重 | 苏杭 | 北戴河 | 桂林 | |
|---|---|---|---|---|
| 景色 | \(\color{Salmon}{0.5954}\) | \(\color{Salmon}{0.2764}\) | \(\color{Salmon}{0.1283}\) | |
| 花费 | ||||
| 居住 | ||||
| 饮食 | ||||
| 交通 |
代码演示
(具体代码详讲在视频后半段)
| 景色 | 花费 | 居住 | 饮食 | 交通 | |
|---|---|---|---|---|---|
| 景色 | \(1\) | \(\frac{1}{2}\) | \(4\) | \(3\) | \(3\) |
| 花费 | \(2\) | \(1\) | \(8\) | \(6\) | \(6\) |
| 居住 | \(\frac{1}{4}\) | \(\frac{1}{8}\) | \(1\) | \(\frac{3}{4}\) | \(\frac{3}{4}\) |
| 饮食 | \(\frac{1}{3}\) | \(\frac{1}{6}\) | \(\frac{4}{3}\) | \(1\) | \(1\) |
| 交通 | \(\frac{1}{3}\) | \(\frac{1}{6}\) | \(\frac{4}{3}\) | \(1\) | \(1\) |
求上面这个判断矩阵的权重
代码文件名称:ccfx.m(提取码:ncst)