A - Candies
Time limit: 1000 ms
Memory limit: 262144 kB
Source: Codeforces Round #636 (Div. 3)
Tags: brute force math *900
Editorial: Announcement Tutorial
Recently Vova found \(n\) candy wrappers. He remembers that he bought \(x\) candies during the first day, \(2x\) candies during the second day, \(4x\) candies during the third day, …, \(2^{k−1}x\) candies during the \(k\)-th day. But there is an issue: Vova remembers neither \(x\) nor \(k\) but he is sure that \(x\) and \(k\) are positive integers and \(k>1\).
Vova will be satisfied if you tell him any positive integer \(x\)
so there is an integer \(k>1\) that \(x+2x+4x+⋯+2^{k−1}x=n\). It is guaranteed that at least one solution exists. Note that \(k>1\).
You have to answer \(t\)independent test cases.
Input
The first line of the input contains one integer \(t(1 \leqslant t \leqslant 10^4)\) — the number of test cases. Then \(t\) test cases follow.
The only line of the test case contains one integer \(n(3 \leqslant n \leqslant 10^9)\) — the number of candy wrappers Vova found. It is guaranteed that there is some positive integer \(x\) and integer \(k>1\) that \(x+2x+4x+⋯+2^{k−1}x=n\).
Output
Print one integer — any positive integer value of \(x\) so there is an integer \(k>1\) that \(x+2x+4x+⋯+2^{k−1}x=n\).
Example
Input
7
3
6
7
21
28
999999999
999999984
Output
1
2
1
7
4
333333333
333333328
Note
In the first test case of the example, one of the possible answers is \(x=1,k=2\). Then \(1⋅1+2⋅1\) equals \(n=3\).
In the second test case of the example, one of the possible answers is \(x=2,k=2\). Then \(1⋅2+2⋅2\) equals \(n=6\).
In the third test case of the example, one of the possible answers is \(x=1,k=3\). Then \(1⋅1+2⋅1+4⋅1\) equals \(n=7\).
In the fourth test case of the example, one of the possible answers is \(x=7,k=2\)
. Then \(1⋅7+2⋅7\) equals \(n=21\).
In the fifth test case of the example, one of the possible answers is \(x=4,k=3\)
. Then \(1⋅4+2⋅4+4⋅4\) equals \(n=28\).
题目大意
对于式子\(x+2x+4x+⋯+2^{k−1}x=n\),已知\(n\),求\(x\)(\(n,x,k\)均为正整数,只要求\(k>1\))。
PZ's Solution
直接累加\(2^{k-1}\),尝试能否整除\(n\)即可;
- TAG:数学
PZ.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,sum,pre2;
int main(){
int T; scanf("%d",&T); while(T--){
scanf("%d",&n);
sum=3; pre2=4;
while(n%sum){
sum+=pre2;
pre2*=2;
}
printf("%d\n",n/sum);
}
return 0;
}
B - Balanced Array
Time limit: 1000 ms
Memory limit: 262144 kB
Source: Codeforces Round #636 (Div. 3)
Tags: constructive algorithms math *800
Editorial: Announcement Tutorial
You are given a positive integer \(n\), it is guaranteed that \(n\) is even (i.e. divisible by \(2\)).
You want to construct the array \(a\) of length \(n\) such that:
- The first \(\frac{n}{2}\) elements of \(a\) are even (divisible by \(2\));
- the second \(\frac{n}{2}\) elements of \(a\) are odd (not divisible by \(2\));
- all elements of \(a\) are distinct and positive;
- the sum of the first half equals to the sum of the second half (\(\sum_{i=1}^{\frac{n}{2}}a_i=\sum_{i=\frac{n}{2}+1}^{n}a_i\)).
If there are multiple answers, you can print any. It is not guaranteed that the answer exists.
You have to answer \(t\) independent test cases.
Input
The first line of the input contains one integer \(t(1 \leqslant t \leqslant 10^4)\) — the number of test cases. Then \(t\) test cases follow.
The only line of the test case contains one integer \(n(2 \leqslant n \leqslant 2⋅10^5)\) — the length of the array. It is guaranteed that that \(n\) is even (i.e. divisible by \(2\)).
It is guaranteed that the sum of \(n\) over all test cases does not exceed \(2⋅10^5\) (\(\sum n \leqslant 2⋅10^5\)).
Output
For each test case, print the answer — NO (without quotes), if there is no suitable answer for the given test case or YES in the first line and any suitable array \(a_1,a_2,…,a_n\)(\(1\leqslant a_i \leqslant 10^9\)) satisfying conditions from the problem statement on the second line.
Example
Input
5
2
4
6
8
10
Output
NO
YES
2 4 1 5
NO
YES
2 4 6 8 1 3 5 11
NO
题目大意
要求构造一个长度为\(n\)(\(n\)为偶数)的数列\(a\),要求:
-
前\(\frac{n}{2}\)项均为偶数;
-
后\(\frac{n}{2}\)项均为奇数;
-
数列元素要求各不相同;
-
前\(\frac{n}{2}\)项和 等于 后\(\frac{n}{2}\)项和(即\(\sum_{i=1}^{\frac{n}{2}}a_i=\sum_{i=\frac{n}{2}+1}^{n}a_i\));
PZ's Solution
1.首先考虑何种情况无法构造出数列,考虑到:
奇数+奇数=偶数,偶数+奇数=奇数,偶数+偶数=偶数,
说明如果\(\frac{n}{2}\)是奇数,则 奇数个奇数相加,只可能是奇数;但 奇数个偶数相加,只可能是偶数;
这样,可以判断出如果\(\frac{n}{2}\)是奇数,则数列\(a\)不可能被构造出来;
2.如何构造数列?实际上乱搞就可以了,偶数可以使用\(2,4,6,8,\cdots\)乱搞一波;
然后奇数就使用\(1,3,5,7,\cdots\),最后一位可以结合偶数部分计算,
因为偶数相对应的每个数都大\(1\),所以最后一个数直接在规律基础上加上\(\frac{n}{2}\)即可;
- TAG:构造
PZ.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n;
int main(){
int T; scanf("%d",&T); while(T--){
scanf("%d",&n);
if((n/2)%2==1){ puts("NO"); continue; }
else puts("YES");
int x=2;
for(int i=1;i<=n/2;++i){
printf("%d ",x);
x+=2;
}
int y=1;
for(int i=1;i<n/2;++i){
printf("%d ",y);
y+=2;
}
printf("%d\n",y+n/2);
}
return 0;
}
C - Alternating Subsequence
Time limit: 1000 ms
Memory limit: 262144 kB
Source: Codeforces Round #636 (Div. 3)
Tags: dp greedy two pointers *1200
Editorial: Announcement Tutorial
Recall that the sequence \(b\) is a a subsequence of the sequence \(a\) if \(b\) can be derived from \(a\) by removing zero or more elements without changing the order of the remaining elements. For example, if \(a=[1,2,1,3,1,2,1]\), then possible subsequences are: \([1,1,1,1], [3]\) and \([1,2,1,3,1,2,1]\), but not \([3,2,3]\) and \([1,1,1,1,2]\).
You are given a sequence \(a\) consisting of \(n\) positive and negative elements (there is no zeros in the sequence).
Your task is to choose maximum by size (length) alternating subsequence of the given sequence (i.e. the sign of each next element is the opposite from the sign of the current element, like positive-negative-positive and so on or negative-positive-negative and so on). Among all such subsequences, you have to choose one which has the maximum sum of elements.
In other words, if the maximum length of alternating subsequence is \(k\)
then your task is to find the maximum sum of elements of some alternating subsequence of length \(k\).
You have to answer \(t\)independent test cases.
Input
The first line of the input contains one integer \(t(1 \leqslant t \leqslant 10^4)\) — the number of test cases. Then \(t\) test cases follow.
The first line of the test case contains one integer \(n(1 \leqslant n \leqslant 2⋅10^5)\) — the number of elements in \(a\). The second line of the test case contains \(n\) integers \(a_1,a_2,…,a_n (−10^9 \leqslant a_i \leqslant 10^9,a_i≠0)\), where \(a_i\) is the \(i\)-th element of \(a\).
It is guaranteed that the sum of \(n\) over all test cases does not exceed \(2⋅10^5 (\sum n \leqslant 2⋅10^5)\).
Output
For each test case, print the answer — the maximum sum of the maximum by size (length) alternating subsequence of \(a\).
Example
Input
4
5
1 2 3 -1 -2
4
-1 -2 -1 -3
10
-2 8 3 8 -4 -15 5 -2 -3 1
6
1 -1000000000 1 -1000000000 1 -1000000000
Output
2
-1
6
-2999999997
Note
In the first test case of the example, one of the possible answers is \([1,2,\underline{3},\underline{−1},−2]\).
In the second test case of the example, one of the possible answers is \([−1,−2,\underline{−1},−3]\).
In the third test case of the example, one of the possible answers is \([\underline{−2},8,3,\underline{8},\underline{−4},−15,\underline{5},\underline{−2},−3,\underline{1}]\).
In the fourth test case of the example, one of the possible answers is \([\underline{1},\underline{−1000000000},\underline{1},\underline{−1000000000},\underline{1},\underline{−1000000000}]\).
题目大意
给出一个长度为\(n\)的,只包含正数和负数的序列,要求从中选出一个子序列,保证:
1.子序列相邻两项符号相反;
2.子序列的长度为满足1.情况下的最长长度;
3.子序列的和在2.的基础上尽可能大;
PZ's Solution
1.由于题目要求子序列长度最长,可以做这样的处理:
对于当前元素,如果其与前一项元素的符号相反,则答案就可以从 前一项元素所在的相同符号的一段中选择一个最大的元素 累加;
2.随后便是开头和结尾的细节处理即可,这样不仅可以保证长度最长,也可以保证和尽可能大;
- TAG:模拟
PZ.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n,a,res,pre;
long long sum;
int check(int a){ return a>0 ? 1 : -1; }
int main(){
int T;
scanf("%d",&T);
while(T--){
scanf("%d",&n);
pre=sum=0;
for(int i=1;i<=n;++i){
scanf("%d",&a);
if(pre==0) res=a;
if(check(a)!=pre&&pre!=0){
sum+=res;
res=a;
}
else res=max(a,res);
pre=check(a);
}
sum+=res;
printf("%lld\n",sum);
}
return 0;
}
D - Guessing the Greatest (easy version)
Time limit: 1000 ms
Memory limit: 262144 kB
Source: Codeforces Round #703 (Div. 2)
Tags: binary search interactive
Editorial: Announcement Tutorial (en)
The only difference between the easy and the hard version is the limit to the number of queries.
This is an interactive problem.
There is an array \(a\) of \(n\) different numbers. In one query you can ask the position of the second maximum element in a subsegment \(a[l..r]\). Find the position of the maximum element in the array in no more than \(40\) queries.
A subsegment \(a[l..r]\) is all the elements \(a_l,a_{l+1},...,a_r\). After asking this subsegment you will be given the position of the second maximum from this subsegment in the whole array.
Input
The first line contains a single integer \(n (2\leqslant n \leqslant 10^5)\) — the number of elements in the array.
Interaction
You can ask queries by printing ? l r$ (1 \leqslant l<r \leqslant n)$. The answer is the index of the second maximum of all elements \(a_l,a_{l+1},…,a_r\). Array a is fixed beforehand and can't be changed in time of interaction.
You can output the answer by printing ! p, where \(p\) is the index of the maximum element in the array.
You can ask no more than \(40\) queries. Printing the answer doesn't count as a query.
After printing a query do not forget to output end of line and flush the output. Otherwise, you will get Idleness limit exceeded. To do this, use:
fflush(stdout)orcout.flush()in C++;System.out.flush()in Java;flush(output)in Pascal;stdout.flush()in Python;- see documentation for other languages
Hacks
To make a hack, use the following test format.
In the first line output a single integer \(n (2 \leqslant n \leqslant 10^5)\). In the second line output a permutation of n integers \(1\) to \(n\). The position of \(n\) in the permutation is the position of the maximum
Example
Input
5
3
4
Output
? 1 5
? 4 5
! 1
Note
In the sample suppose \(a\) is \([5,1,4,2,3]\). So after asking the \([1..5]\) subsegment \(4\) is second to max value, and it's position is \(3\). After asking the \([4..5]\) subsegment \(2\) is second to max value and it's position in the whole array is \(4\).
Note that there are other arrays \(a\) that would produce the same interaction, and the answer for them might be different. Example output is given in purpose of understanding the interaction.
题目大意
本题为交互题;
给定一个数组\(a\),其大小为\(n\)(下标从\(1\)开始),其中的元素各不相同;
你可以询问一个区间\(a[l,r]\)$ (1 \leqslant l<r \leqslant n)$不超过\(40\)次,每次询问都会给出 该区间第二大值的下标;
通过这些有限次的询问,你需要得出数组\(a\) 中 最大值的下标;
Solution
思路来自cyhforlight的CF Round #703 Div2 解题补题报告
1.题目的描述可以直接猜想到使用二分算法;
2.考虑第二大值的下标对答案有何贡献,设\(x=query(L,R),y=query(L,mid)\),
可以发现,如果\(x=y\),说明在区间\([L,mid]\)存在这个数组的最大值,限制着第二大值的下标不变;
3.用更加具体的操作来表述,设\(x=query(L,R),y=query(L,mid),z=query(mid+1,R)\),可以这样思考:
当\(L \leqslant x \leqslant mid\)时,如果\(x=y\),则最大值一定在\([L,mid]\)之间;如果\(x \not= y\),那么最大值就在\([mid+1,R]\)之间;
当\(mid+1 \leqslant x \leqslant R\)时,如果\(x=z\),则最大值一定在\([mid,R]\)之间;如果\(x \not= y\),那么最大值就在\([L,mid]\)之间;
4.考虑只有两个数的情况,设\(x=query(L,L+1)\),这样第二大值知道后,最大值一定是另一个坐标;
5.考虑只有三个数的情况,设\(x=query(L,R)\),
如果第二大数在\(L\),则直接进入两个数\((L+1,R)\)的情况;
如果第二大数在\(R\),则直接进入两个数\((L,L+1)\)的情况;
如果第二大数在\(L+1\),询问\(y=query(L,L+1)\),如果\(x=y\),回到2.的情况,最大值必为\(L\),否则最大值必为\(R\);
5.注意题目要求每次输出后要清空缓冲区,C++在每次输出后使用fflush(stdout);即可;
- TAG:二分;交互
std.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
int n;
int query(int L,int R){
printf("? %d %d\n",L,R);
fflush(stdout);
int x; scanf("%d",&x);
return x;
}
void Solve2(int L,int R){
int x=query(L,R);
printf("! %d\n",x==L? L+1 : L);
fflush(stdout);
}
int main(){
scanf("%d",&n);
int L=1,R=n;
while(L<R){
if(R-L+1==2){
Solve2(L,R);
return 0;
}
if(R-L+1==3){
int x=query(L,R);
if(x==L) Solve2(L+1,R);
if(x==R) Solve2(L,L+1);
if(x==L+1){
int y=query(L,L+1);
printf("! %d\n",x==y ? L : R);
fflush(stdout);
}
return 0;
}
int mid=L+R>>1;
int x=query(L,R);
if(L<=x&&x<=mid){
int y=query(L,mid);
if(x==y) R=mid;
else L=mid+1;
} else {
int y=query(mid+1,R);
if(x==y) L=mid+1;
else R=mid;
}
}
printf("! %d\n",L);
fflush(stdout);
return 0;
}
E - Constant Palindrome Sum
Time limit: 1000 ms
Memory limit: 262144 kB
Source: Codeforces Round #636 (Div. 3)
Tags: brute force data structures greedy two pointers *1700
Editorial: Announcement Tutorial
You are given an array \(a\) consisting of \(n\) integers (it is guaranteed that \(n\) is even, i.e. divisible by \(2\)). All \(a_i\) does not exceed some integer \(k\).
Your task is to replace the minimum number of elements (replacement is the following operation: choose some index \(i\) from \(1\) to \(n\) and replace \(a_i\) with some integer in range \([1,k]\)) to satisfy the following conditions:
- after all replacements, all \(a_i\) are positive integers not greater than \(k\);
- for all \(i\) from \(1\) to \(\frac{n}{2}\) the following equation is true: \(a_i+a_{n−i+1}=x\), where \(x\) should be the same for all \(\frac{n}{2}\) pairs of elements.
You have to answer \(t\) independent test cases.
Input
The first line of the input contains one integer \(t (1 \leqslant t \leqslant 10^4)\) — the number of test cases. Then \(t\) test cases follow.
The first line of the test case contains two integers \(n\) and \(k (2\leqslant n \leqslant 2⋅10^5,1 \leqslant k \leqslant 2⋅10^5)\) — the length of \(a\) and the maximum possible value of some \(a_i\) correspondingly. It is guaranteed that \(n\) is even (i.e. divisible by \(2\)). The second line of the test case contains \(n\) integers \(a_1,a_2,…,a_n (1 \leqslant a_i \leqslant k)\), where \(a_i\) is the \(i\)-th element of \(a\).
It is guaranteed that the sum of \(n\) (as well as the sum of \(k\)) over all test cases does not exceed \(2⋅10^5 (\sum n \leqslant 2⋅10^5, \sum k \leqslant 2⋅10^5)\).
Output
For each test case, print the answer — the minimum number of elements you have to replace in \(a\) to satisfy the conditions from the problem statement.
Example
Input
4
4 2
1 2 1 2
4 3
1 2 2 1
8 7
6 1 1 7 6 3 4 6
6 6
5 2 6 1 3 4
Output
0
1
4
2
题目大意
给定义一个 正整数 数组\(a\),大小为\(n\)(\(n\)为偶数);给定正整数\(k\),保证\(a_i \leqslant k\);
你可以任意次修改数组的任意一个数,将此数变为\([1,k]\)之间的任意一个数,要求:
修改操作结束后,对于任意\(i \in [1,\frac{n}{2}]\),都有\(a_i+a_{n−i+1}=x\),\(x\)为一定值;
求修改操作的最少次数;
Solution
思路来自StelaYuri的Codeforces 1343D - Constant Palindrome Sum (差分数组)
1.考虑使用 差分数组\(S\),对于每对\(a_i,a_{n-i+1}\),设\(sum=a_i+a_{n-i+1},a_{min}=min(a_i,a_{n-i+1}),a_{max}=max(a_i,a_{n-i+1})\);
2.进行分类讨论:
1).如果\(x\)在\([2,a_{min}]\)之间,即使将\(a_{max}\)改为\(1\),和也为\(a_{min}+1 >x\),故两个数都需要修改,即差分数组\(S\)的\([2,a_{min}]+2\);
2).如果\(x\)在\([a_{min}+1,a_{max}+k]\)之间,则只需要将其中一个值改变即可满足要求,特殊的,如果此时\(x=sum\),则不需要修改操作,即差分数组\(S\)的\([a_{min}+1,sum-1]+1,[sum+1,a_{max}+k]+1\);
3).如果\(x\)在\([a_{max}+k+1,2*k]\)之间,即使将\(a_{min}\)改为\(k\),和也为\(a_{max}+k<x\),故两个数都需要修改,差分数组\(S\)的\([a_{max}+k+1,2*k]+2\);
3.通过分类讨论,可以得出差分数组的处理代码:
S[2]+=2;
S[amin+1]-=2;
//对应1)
S[amin+1]+=1;
S[sum]-=1;
S[sum+1]+=1;
S[amax+k+1]-=1;
//对应2)
S[amax+k+1]+=2;
S[2*k+1]-=2;
//对应3)
4.整理差分数组的处理代码,利用前缀和,这时差分数组的前缀和意义为 当定值为\(x\)时需要的修改次数,寻找最小值即可;
- TAG:差分
std.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<climits>
using namespace std;
const int N=2e5+10;
int T,n,k,ans,sum,maxa,mina,a[N],s[2*N];
int main(){
scanf("%d",&T);
while(T--){
ans=INT_MAX;
memset(s,0,sizeof(s));
scanf("%d %d",&n,&k);
for(int i=1;i<=n;++i){
scanf("%d",&a[i]);
if(i>n/2){
sum=a[i]+a[n-i+1];
mina=min(a[i],a[n-i+1]);
maxa=max(a[i],a[n-i+1]);
s[2]+=2;
s[mina+1]--;
s[sum]--;
s[sum+1]++;
s[maxa+k+1]++;
s[2*k+1]-=2;
}
}
for(int i=2;i<=2*k;++i){
s[i]=s[i-1]+s[i];
ans=min(ans,s[i]);
}
printf("%d\n",ans);
}
return 0;
}
F - Weights Distributing
Time limit: 2000 ms
Memory limit: 262144 kB
Source: Codeforces Round #636 (Div. 3)
Tags: brute force graphs greedy shortest paths sortings *2100
Editorial: Announcement Tutorial
You are given an undirected unweighted graph consisting of \(n\) vertices and \(m\) edges (which represents the map of Bertown) and the array of prices \(p\) of length \(m\). It is guaranteed that there is a path between each pair of vertices (districts).
Mike has planned a trip from the vertex (district) \(a\) to the vertex (district) \(b\) and then from the vertex (district) \(b\) to the vertex (district) \(c\). He can visit the same district twice or more. But there is one issue: authorities of the city want to set a price for using the road so if someone goes along the road then he should pay the price corresponding to this road (he pays each time he goes along the road). The list of prices that will be used \(p\) is ready and they just want to distribute it between all roads in the town in such a way that each price from the array corresponds to exactly one road.
You are a good friend of Mike (and suddenly a mayor of Bertown) and want to help him to make his trip as cheap as possible. So, your task is to distribute prices between roads in such a way that if Mike chooses the optimal path then the price of the trip is the minimum possible. Note that you cannot rearrange prices after the start of the trip.
You have to answer \(t\) independent test cases.
Input
The first line of the input contains one integer \(t (1\leqslant t \leqslant 10^4)\) — the number of test cases. Then \(t\) test cases follow.
The first line of the test case contains five integers \(n,m,a,b\) and \(c (2 \leqslant n \leqslant 2⋅10^5, n−1 \leqslant m \leqslant min(\frac{n(n−1)}{2},2⋅10^5), 1 \leqslant a,b,c \leqslant n)\) — the number of vertices, the number of edges and districts in Mike's trip.
The second line of the test case contains \(m\) integers \(p_1,p_2,…,p_m (1 \leqslant p_i \leqslant 10^9)\), where \(p_i\) is the \(i\)-th price from the array.
The following \(m\) lines of the test case denote edges: edge \(i\) is represented by a pair of integers \(v_i, u_i (1≤v_i,u_i≤n, u_i≠v_i)\), which are the indices of vertices connected by the edge. There are no loops or multiple edges in the given graph, i. e. for each pair \((v_i,u_i)\) there are no other pairs \((v_i,u_i)\) or \((u_i,v_i)\) in the array of edges, and for each pair \((v_i,u_i)\) the condition \(v_i≠u_i\) is satisfied. It is guaranteed that the given graph is connected.
It is guaranteed that the sum of \(n\) (as well as the sum of \(m\)) does not exceed \(2⋅10^5 (\sum n \leqslant 2⋅10^5 , \sum m \leqslant 2⋅10^5)\).
Output
For each test case, print the answer — the minimum possible price of Mike's trip if you distribute prices between edges optimally.
Example
Input
2
4 3 2 3 4
1 2 3
1 2
1 3
1 4
7 9 1 5 7
2 10 4 8 5 6 7 3 3
1 2
1 3
1 4
3 2
3 5
4 2
5 6
1 7
6 7
Output
7
12
Note
One of the possible solution to the first test case of the example:
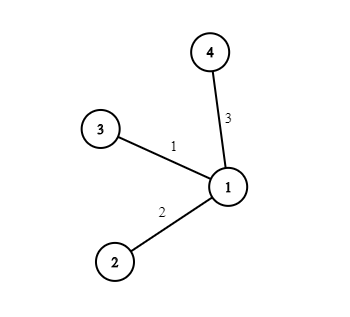
One of the possible solution to the second test case of the example:
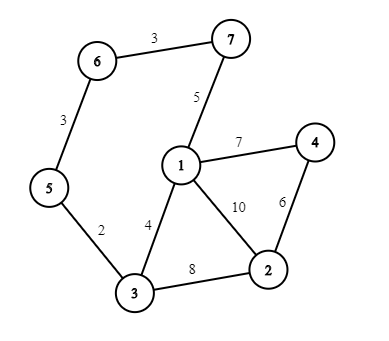
题目大意
给定一个\(n\)个点\(m\)条边的无向图,其不包含环、重边、自环,给出\(m\)个边权,可以任意分配给每条边;
给定三个点\(a,b,c\),要求寻找一条路径(可以重复走 走过的路)满足\(a \rightarrow b \rightarrow c\),并且使用恰当的分配方法使得路径费用最少(重复的路段按重复次数收费);
Solution
思路来自我永远相信赵安之的CF1343E Weights Distributing(BFS+贪心)
1.第一种情况,直接找到一条没有重复道路的\(a \rightarrow b \rightarrow c\)的道路;
2.第二种情况,\(a \rightarrow b \rightarrow c\)的道路有重复的情况,则或多或少必然有一个点\(x\)被遍历过两次;
3.对于第二种情况,有\(a \rightarrow x \rightarrow b \rightarrow x \rightarrow c\),可以发现重复的边只有\(x \rightarrow b \rightarrow x\),那么考虑使用BFS;
3.先只考虑边数,对\(a,b,c\)三个起点进行BFS,记录每个点分别到\(a,b,c\)的最短边数;
4.对边权进行从小到大排序,方便分配的边权最小,并处理出前缀和\(sum\);
5.设\(dis[x][a,b,c]\)分别为\(a,b,c\)到点\(x\)的边数处理出来后,答案即为:
因为\(x \rightarrow b\)等价于\(b \rightarrow x\),所以实际为\(b \rightarrow x\)被计算了两次,为了保证边权和最小,有了上式;
6.实际上,第一种情况是第二种情况的特例,即\(x\)等同于\(b\),而\(b\)到自己当然没有路径,\(dis[b][b]=0\),5.的式子也成立;
- TAG:贪心;BFS广度优先搜索
std.cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
#define N 200005
#define int long long
int n,m,a,b,c,T,p[N],dis[N][5];
int ans,sump[N];
bool vis[N];
vector<int>e[N];
queue<int>q;
void bfs(int u,int x){
for(int i=1;i<=n;++i) vis[i]=0;
q.push(u); dis[u][x]=0; vis[u]=1;
while(!q.empty()){
u=q.front(); q.pop();
for(int v,i=0;i<e[u].size();++i){
v=e[u][i];
if(!vis[v]){
dis[v][x]=dis[u][x]+1;
q.push(v); vis[v]=1;
}
}
}
}
signed main(){
scanf("%lld",&T);
while(T--){
ans=0x3f3f3f3f3f3f3f3f;
scanf("%lld %lld %lld %lld %lld",&n,&m,&a,&b,&c);
for(int i=1;i<=m;++i) scanf("%lld",&p[i]);
sort(p+1,p+1+m);
for(int u,v,i=1;i<=m;++i){
sump[i]=sump[i-1]+p[i];
scanf("%lld %lld",&u,&v);
e[u].push_back(v);
e[v].push_back(u);
}
bfs(a,1);
bfs(b,2);
bfs(c,3);
for(int i=1;i<=n;++i){
if(dis[i][1]+dis[i][2]+dis[i][3]>m) continue;
ans=min(ans,sump[dis[i][1]+dis[i][2]+dis[i][3]]+sump[dis[i][2]]);
}
printf("%lld\n",ans);
for(int i=1;i<=n;++i) e[i].clear();
}
return 0;
}