2018牛客多校第五场

A.gpa（01分数规划）

题意：

　　有n门科目。第i门科目的学分为S_i，分数为C_i。根据学校的规定，最终的得分为 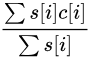。求删掉k门科目后的最大得分。

题解：

　　二分答案，假设当前二分的答案为P，排序求出S_i*(C_i-P)值前n-k大的科目判断可行性。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5+10;
double eps = 1e-8;
int n, k;
double p;
double l, r;
struct node {
    double s, c;
    bool operator < (const node &x) {
        return s*(c-p) > x.s*(x.c-p);
    }
}a[N];
bool check(double x) {
    p = x;
    sort(a+1, a+n+1);
    double res = 0;
    for(int i = 1; i <= n-k; i++) res += a[i].s*(a[i].c-x);
    if(res >= eps) return 1;
    return 0;
}
int main() {
    scanf("%d%d", &n, &k);
    for(int i = 1; i <= n; i++) scanf("%lf", &a[i].s);
    for(int i = 1; i <= n; i++) {
        scanf("%lf", &a[i].c);
        r = max(r, a[i].c);
    }
    for(int i = 1; i <= 100; i++) {
        double mid = (l+r)/2.0;
        if(check(mid)) l = mid+eps;
        else r = mid-eps;
    }
    printf("%.11lf", l);
}

B.div

题意：

　　给出m(1<=m<=10¹⁰⁰⁰)。求出不小于m的n的最小值，使得存在一个x∈[n²+1,n²+2n]且x|n⁴。

题解：

　　假设(n²+a)|n⁴。因为(n²+a)|(n²+a)*(n²-a)，所以(n²+a)|n⁴-(n²+a)*(n²-a)。n⁴-(n²+a)*(n²-a) = a²，所以(n²+a)|a²。

　　令a² = t(n²+a)，因为a²<=4n²<4(n²+a)，所以t = 1，2，3。

　　t = 1时，a² = n²+a，a*(a-1) = n²，无解。

　　t = 2时，n_k+2 = 6n_k+1-n_k。(n₀ = 0，n₁ = 2)

　　t = 3时，n_k+2 = 14n_k+1-n_k。(n₀ = 0，n₁ = 6)

　　(假装自己会python)

m = int(input())
a, b = 0, 2
c, d = 0, 6
while m > b:
    a, b = b, 6*b-a
while m > d:
    c, d = d, 14*d-c
print(min(b, d))

C.grf

留坑。

D.inv（线段树+树状数组）

题意：

　　给出一个偶数n以及1~n之间偶数的排列。将1~n之间的奇数插入排列中，求最小的逆序数。

题解：

　　按从小到大的顺序插入每个奇数，很容易看出每个奇数都是在前一个奇数的后面插入。

　　有m = n/2 个偶数，m+1个插入位置。用m+1个位置插入1时的逆序数初始化线段树。

　　每插入一个新的数时进行区间加减，然后求出最小值更新答案。

　　例如插入3时，3在m+1个位置中的逆序数情况用1的情况来更新。把2位置前面的区间+1，后面的区间-1即为3的情况。

　　还要用树状数组维护求出m个偶数自身的逆序数。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5+10;
int n, m, k;
ll ans;
int pos[N<<1], tre[N];
int minn[N<<2], lzy[N<<2];
void push_up(int id) {
    minn[id] = min(minn[id<<1], minn[id<<1|1]);
}
void build(int id, int l, int r) {
    if(l == r) {
        minn[id] = l-1;
        return ;
    }
    int mid = l+r>>1;
    build(id<<1, l, mid);
    build(id<<1|1, mid+1, r);
    push_up(id);
}
void push_down(int id) {
    lzy[id<<1] += lzy[id];
    lzy[id<<1|1] += lzy[id];
    minn[id<<1] += lzy[id];
    minn[id<<1|1] += lzy[id];
    lzy[id] = 0;
}
void update(int id, int l, int r, int ql, int qr, int val) {
    if(ql<=l && r<=qr) {
        lzy[id] += val;
        minn[id] += val;
        return ;
    }
    if(lzy[id]) push_down(id);
    int mid = l+r>>1;
    if(ql <= mid) update(id<<1, l, mid, ql, qr, val);
    if(qr > mid) update(id<<1|1, mid+1, r, ql, qr, val);
    push_up(id);
}
void add(int pos) {
    while(pos > 0) {
        tre[pos]++;
        pos -= pos&(-pos);
    }
}
int sum(int pos) {
    int res = 0;
    while(pos <= n) {
        res += tre[pos];
        pos += pos&(-pos);
    }
    return res;
}
int main() {
    scanf("%d", &n);
    n >>= 1;
    for(int i = 1; i <= n; i++) {
        scanf("%d", &k);
        ans += sum(k>>1);
        add(k>>1);
        pos[k] = i;
    }
    build(1, 1, n+1);
    for(int i = 2; i <= n; i++) {
        int num = 2*i-2;
        update(1, 1, n+1, 1, pos[num], 1);
        update(1, 1, n+1, pos[num]+1, n+1, -1);
        ans += minn[1];
    }
    printf("%lld
", ans);
} 

E.room（费用流）

题意：

　　一共有n个宿舍，每个宿舍有4个人。给出第一年的人员分布和第二年的人员分布，问至少有多少人需要移动。

题解：

　　2018牛客多校第五场 E.room

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 205;
const int INF = 0x3f3f3f3f;
int n, k;
int x[405], y[405];
int g[105][5];
typedef pair<int, int> P;
struct edge { int to, cap, cost, rev; };
int V; 
vector<edge> G[N];         
int h[N];               
int dist[N];       
int prevv[N], preve[N];  
void add_edge(int from, int to, int cap, int cost) {
    G[from].push_back((edge){to, cap, cost, (int)G[to].size()});
    G[to].push_back((edge){from, 0, -cost, (int)G[from].size()-1});
}
int min_cost_flow(int s, int t, int f) {
    int res = 0;
    fill(h, h + V, 0);
    while(f > 0) {
        priority_queue<P, vector<P>, greater<P> > que;
        fill(dist, dist + V, INF);
        dist[s] = 0;
        que.push(P(0, s));
        while(!que.empty()) {
            P p = que.top(); que.pop();
            int v = p.second;
            if(dist[v] < p.first) continue;
            int len = G[v].size();
            for(int i = 0; i < len; i++) {
                edge &e = G[v][i];
                if(e.cap > 0 && dist[e.to] > dist[v] + e.cost + h[v] - h[e.to]) {
                    dist[e.to] = dist[v] + e.cost + h[v] - h[e.to];
                    prevv[e.to] = v;
                    preve[e.to] = i;
                    que.push(P(dist[e.to], e.to));
                }
            }
        }
        if(dist[t] == INF) return -1;
        for(int v = 0; v < V; v++) h[v] += dist[v];
        int d = f;
        for(int v = t; v != s; v = prevv[v]) d = min(d, G[prevv[v]][preve[v]].cap);
        f -= d;
        res += d*h[t];
        for(int v = t; v != s; v = prevv[v]) {
            edge &e = G[prevv[v]][preve[v]];
            e.cap -= d;
            G[v][e.rev].cap += d;
        }
    }
    return res;
}
int main() {
    scanf("%d", &n);
    for(int i  = 1; i <= n; i++)
        for(int j = 1; j <= 4; j++) {
            scanf("%d", &k);
            x[k] = i;
            y[k] = j;
        }
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= 4; j++) {
            scanf("%d", &k);
            g[x[k]][y[k]] = i;
        }
    for(int i = 1; i <= n; i++) add_edge(0, i, 1, 0);
    for(int i = n+1; i <= 2*n; i++) add_edge(i, 2*n+1, 1, 0);
    for(int i = 1; i <= n; i++) {
        for(int j = n+1; j <= 2*n; j++) {
            int cnt = 4;
            for(int k = 1; k <= 4; k++) if(g[i][k] == j-n) cnt--;
            add_edge(i, j, 1, cnt);
        }
    }
    V = 2*n+2;
    printf("%d
", min_cost_flow(0, 2*n+1, n));
}

F.take

题意：

　　有n个盒子，每个盒子有p_i的概率有一颗大小为d_i的钻石。初始时有一颗大小为0的钻石，从小到大开盒子，每开到比当前钻石大的钻石就会交换一次。求交换次数的期望值。

题解：

　　求出每个盒子的期望值，最终求和。用树状数组维护每个盒子前面比他大的钻石的(1-p_i)的积。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5+10;
const int mod = 998244353;
int n;
int ans;
int id[N];
int tre[N];
struct node {
    int p, d;
}a[N];
void add(int pos, int val) {
    while(pos > 0) {
        tre[pos] = (1ll*tre[pos]*val)%mod;
        pos -= pos&(-pos);
    }
}
int sum(int pos) {
    int res = 1;
    while(pos <= n) {
        res = (1ll*res*tre[pos])%mod;
        pos += pos&(-pos);
    }
    return res;
}
ll quick_mod(int n, int m) {
    int res = 1, t = n;
    while(m) {
        if(m & 1) res = (1ll * res * t) % mod;
        t = (1ll * t * t) % mod;
        m >>= 1;
    }
    return res;
}
int main() {
    scanf("%d", &n);
    int inv = quick_mod(100, mod-2);
    for(int i = 1; i <= n; i++) {
        scanf("%d%d", &a[i].p, &a[i].d);
        id[i] = a[i].d;
        tre[i] = 1;
    }
    sort(id + 1, id + n + 1);
    for(int i = 1; i <= n; i++) {
        int p = lower_bound(id+1, id+n+1, a[i].d)-id;
        ans += (1ll * sum(p+1) * a[i].p % mod) * inv % mod;
        ans %= mod;
        add(p, 1ll*(100-a[i].p)*inv%mod);
    }
    printf("%d
", ans);
}

G.max

题意：

　　给出c，n。求不大于n的两个数的最大乘积，使得两个数的最大公约数为c。

题解：

　　有一个性质是数k和k-1是互质的。

　　所以n<c时无解。 n/c = 1时两个数都为n/c*c。 否则两个数为n/c*c和(n/c-1)*c。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int c, n;
int main() {
    scanf("%d%d", &c, &n);
    if(c > n) {
        puts("-1");
        return 0;
    }
    n /= c;
    if(n == 1) printf("%lld
", 1ll*c*c);
    else printf("%lld
", 1ll*c*c*n*(n-1));
}

H.subseq（树状数组）

题意：

　　给出a数组的排列。求出字典序第k小的b数组的排列，满足1<=b_i<=n，b_i<b_i+1，a[b[i]]<a[b[i+1]]，m>0。

题解：　

　　2018牛客多校第五场 H.subseq

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5e5+10;
const ll inf = 1e18+10;
int n, tot, pre;
ll k, sum;
int a[N], id[N], ans[N];
ll tre[N], val[N];
ll add(ll x, ll y) { return min(x + y, inf); }
void update(int pos, ll val) {
    while(pos > 0) {
        tre[pos] = add(tre[pos], val);
        pos -= pos&(-pos);
    }
}
ll query(int pos) {
    ll res = 0;
    while(pos <= n) {
        res = add(res, tre[pos]);
        pos += pos&(-pos);
    }
    return res;
}
int main() {
    scanf("%d%lld", &n, &k);
    for(int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        id[i] = a[i];
    }
    sort(id+1, id+n+1);
    for(int i = n; i >= 1; i--) {
        int p = lower_bound(id+1, id+n+1, a[i])-id;
        val[i] = query(p+1)+1;
        update(p, val[i]);
    }
    for(int i = 1; i <= n; i++) sum = add(sum, val[i]);
    if(sum < k) {
        puts("-1");
        return 0;
    }
    for(int i = 1; i <= n; i++) {
        if(k == 0) break;
        if(a[i] <= a[pre]) continue;
        if(val[i] < k) k -= val[i];
        else {
            ans[++tot] = i;
            k--;
            pre = i;
        }
    }
    printf("%d
", tot);
    for(int i = 1; i < tot; i++) printf("%d ", ans[i]);
    printf("%d
", ans[tot]);
}

I.vcd（树状数组）

题意：　

　　定义一个无限的集合H为{(x,y)|x>=a,l<=y<=r}，其中a，l，r为任意值。给出n个坐标点。求出有多少个点集S，使得S的任意一个子集T满足H∩S = T。

题解：

　　画图可以分析出点集S一共只有3种情况，即点数不可能大于3。

　　1、包含一个点时，共有n种。

　　2、包含二个点时，从1~n扫一遍，每次加上前面（点的个数 - 和他纵坐标相同的个数）

　　3、包含三个点时，这三个点呈<号状。将这n个点按照x排序，每次加上前面（横坐标不等于当前点&&纵坐标大于当前点）*（横坐标不等于当前点&&纵坐标小于当前点）的个数。

　　对于横坐标不等于当前点的要求，可以在当前点的横坐标不等于上一个点的横坐标时再更新所有跟上一个点横坐标相等的点。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5+10;
const int mod = 998244353;
int n;
int ans;
int id[N], vis[N];
int tre[N];
struct node {
    int x, y;
    bool operator < (const node &a) {
        return x > a.x;
    }
}a[N];
void add(int pos) {
    while(pos <= n) {
        tre[pos]++;
        pos += pos&(-pos);
    }
}
int sum(int pos) {
    int res = 0;
    while(pos > 0) {
        res += tre[pos];
        pos -= pos&(-pos);
    }
    return res;
}
int main() {
    scanf("%d", &n);
    ans = n;
    for(int i = 1; i <= n; i++) {
        scanf("%d%d", &a[i].x, &a[i].y);
        id[i] = a[i].y;
    }
    sort(a+1, a+n+1);
    sort(id+1, id+n+1);
    int l = 1;
    for(int i = 1; i <= n; i++) {
        if(i != 1 && a[i].x != a[i-1].x) {
            for(int j = l; j < i; j++) {
                int y = lower_bound(id+1, id+n+1, a[j].y)-id;
                add(y);
            }
            l = i;
        }
        int y = lower_bound(id+1, id+n+1, a[i].y)-id;
        ans = (ans+i-1-vis[y])%mod;
        vis[y]++;
        ans = (1ll*sum(y-1)*(l-1-sum(y))%mod+ans)%mod;
    }
    printf("%d
", ans);
}

J.plan

题意：

　　给出人数，双人间及三人间的费用。求总的最小费用。

题解：

　　　贪心即可。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main() {
    ll ans = 0;
    ll n, p2, p3;
    scanf("%lld%lld%lld", &n, &p2, &p3); 
    if(p2 * 3 <= p3 * 2) {
        ans += p2 * (n / 2);
        if(n & 1) {
            if(p2 * 2 <= p3) ans += p2;
            else ans += p3 - p2;
        }
    }
    else {
        ll cnt = n / 3;
        ll res = n % 3;
        ans += cnt * p3;
        if(res == 2) {
            if(p2 <= p3) ans += p2;
            else ans += p3;
        }
        else if(res == 1) {
            if(p2 <= p3) ans += 2 * p2 - p3;
            else ans += p3;
        }
    }
    printf("%lld
", ans);
}