代码随想录：二叉树的属性

二叉树的深度

递归法获得二叉树的深度

树的深度 -> 后序遍历求根节点的高度 

思路：递归三步骤。求根节点的高度，即最大深度，可以用后序遍历的逻辑

1.确定函数形式，返回类型，参数：输入一个TreeNode,返回一个int深度，so

int getMaxDepth(treeNode * node)

2. 确定终止条件： 如果node为空，就返回0，表示高度为0

if(node == NULL) return 0;

3. 确定递归逻辑：对一个节点而言，看左右子节点返回的高度，哪个高度大作为该节点的返回（+1是加了当前节点的高度1）

int leftDepth = getMaxDepth(node->left);
int rightDepth = getMaxDepth(node->right);
int maxDepth = 1 + max(leftDepth, rightDepth);
return maxDepth;

　　

整合代码

class Solution {
public:
    int getdepth(TreeNode* root) {
        if (root == NULL) return 0;
        int leftdepth = getdepth(root->left);       // 左
        int rightdepth = getdepth(root->right);     // 右
        int depth = 1 + max(leftdepth, rightdepth); // 中
        return depth;
    }
    int maxDepth(TreeNode* root) {
        return getdepth(root);
    }
};

还可以精简代码：

class solution {
public:
    int maxdepth(treenode* root) {
        if (root == null) return 0;
        return 1 + max(maxdepth(root->left), maxdepth(root->right));
    }
};

　

前序遍历求深度

实际上前序遍历才能体现求深度的真正逻辑：

class Solution {
public:
    int result;
    void getdepth(TreeNode* root, int depth){
        //前序遍历 中 左 右
        result = depth > result?depth : result;//中
        if(root->left==NULL &&root->right==NULL) return;
        if(root->left){//左
            depth++;
            getdepth(root->left,depth);
            depth--;//回溯
        }
        if(root->right){//右
            depth++;
            getdepth(root->right,depth);
            depth--;//回溯
        }
        return;
    }

    int maxDepth(TreeNode* root) {
        result = 0;
        if(root==NULL) return result;
        getdepth(root,1);
        return result;
    }
}

　　

上面有步骤可以简化代码：

if(root->left) getDepth(node->left, depth + 1);
if(root->right) getDepth(node->right, depth + 1);

　　

迭代法获得二叉树的深度

 可以用层序遍历法来得到二叉树的最大深度和最小深度

二叉树的最大深度

104. 二叉树的最大深度 - 力扣（LeetCode） (leetcode-cn.com)

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点

思路：层序遍历，当每遍历一层，就把深度加1，当遍历完最后一层，队列为空，退出。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        queue<TreeNode*> queueNode;
        if(root != NULL) queueNode.push(root);
        //空二叉树拳头警告
        //vector<vector<int>> res;
        int depth = 0;
        while(!queueNode.empty()){
            //每次遍历一层，一层的节点在进入while时候确定，后面会改变，所以for循环中不能用size()，而应该用固定长度
            int layerSize = queueNode.size();
            for(int i =0;i<layerSize;i++){
                TreeNode *tempNode = queueNode.front();
                queueNode.pop();
                if(tempNode->left) queueNode.push(tempNode->left);
                if(tempNode->right) queueNode.push(tempNode->right);
            }
            depth+=1;
        }
        return depth;  
    }
};

二叉树的最小深度

111. 二叉树的最小深度 - 力扣（LeetCode） (leetcode-cn.com)

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

错的思路：当某层节点数不为2^(k-1)时，就可能为最小深度

思路：注意，只有当左右孩子都为空的时候，才说明遍历的最低点了。如果其中一个孩子为空则不是最低点

所以只有当某个节点左右孩子都指向NULL，才作为最小深度的层的节点，从顶层往下做，当遇到第一个左右子节点为空时，说明遇到了叶子节点，可直接返回深度

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        queue<TreeNode*> queueNode;
        if(root != NULL) queueNode.push(root);
        if(root == NULL) return 0;
        //空二叉树拳头警告
        //vector<vector<int>> res;
        int minDepth = 1;
        while(!queueNode.empty()){
            //每次遍历一层，一层的节点在进入while时候确定，后面会改变，所以for循环中不能用size()，而应该用固定长度
            int layerSize = queueNode.size();
            
            for(int i =0;i<layerSize;i++){
                TreeNode *tempNode = queueNode.front();
                queueNode.pop();
                if(tempNode->left) queueNode.push(tempNode->left);
                if(tempNode->right) queueNode.push(tempNode->right);
                if(!tempNode->left && !tempNode->right) return minDepth;
            }
            minDepth+=1;
        }
        return minDepth;  
    }
};

对称二叉树

101. 对称二叉树 - 力扣（LeetCode） (leetcode-cn.com)

也叫镜像二叉树，即判断给定root的二叉树是不是镜像/对称的。

对称的二叉树：

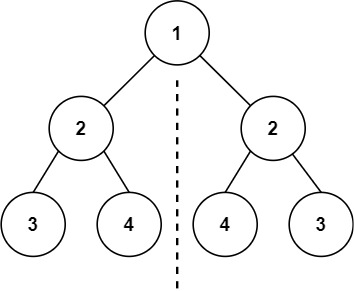
不对称的二叉树：

 

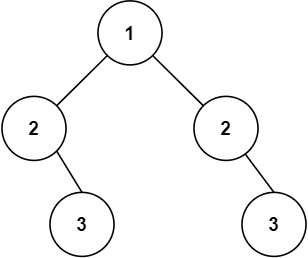
递归判断对称二叉树

思路：递归。

关于中间对称轴对称的两节点是否相同，而不仅仅是左右节点相同。so比较对称的两棵子树是否是相互翻转的。。

一个递归 左右中，一个递归 右左中，来比较对称的子树（左边看和右边看过去是一样的）

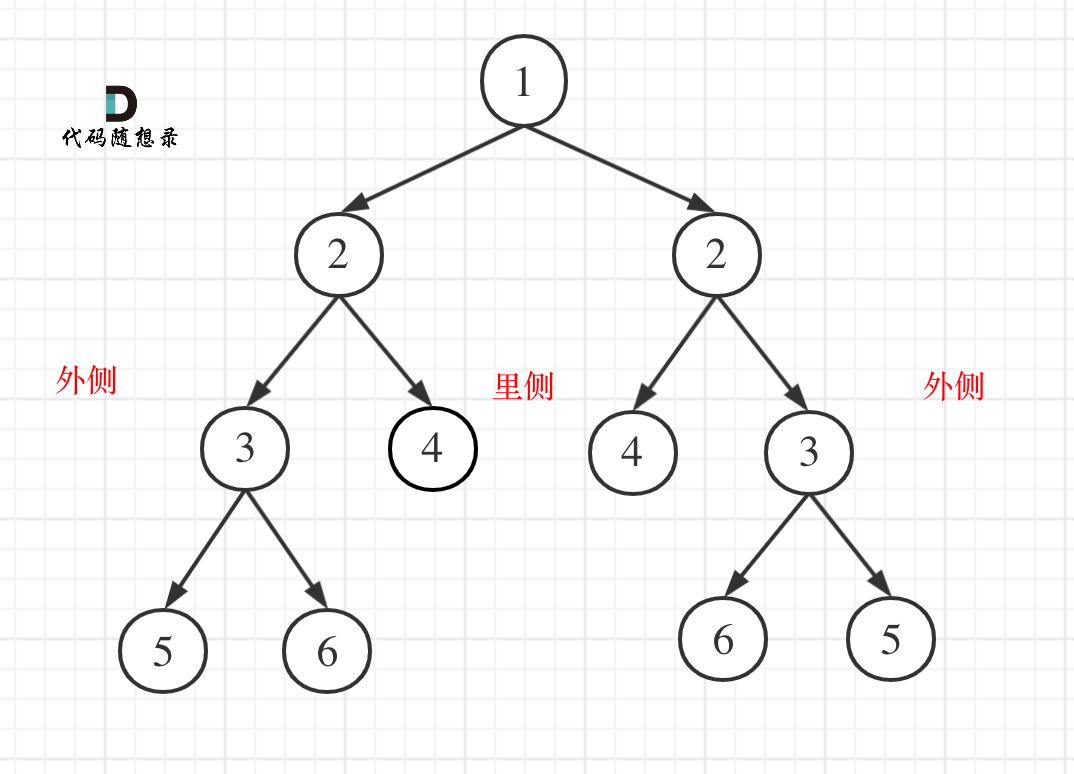
既然是递归方法，递归三部曲：背（确定函数参数和返回值，确定终止条件，确定递归逻辑）

确定函数参数和返回值

这里，要递归比较两棵对称的子树是否是相互翻转，参数为两棵子树的root，返回值是true 或者false.

bool cmp(TreeNode * left, TreeNode * right){
    //递归函数
}

确定终止条件

什么时候不对称呢返回false？外侧空节点不对称，内测空节点不对称，当前root的val不相等

什么时候对称呢返回true？左右节点都不为空，且数值相同的情况(p.s. 另外还有一种情况，左右子树都为空，即到了叶子节点)

if(left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left->val != right->val) return false;
else if (left == NULL && right == NULL) return true;

确定递归逻辑

处理左右子树都不为空，且数值相同的情况。

要递归比较左子树的外侧和右子树的外侧 left->left vs right->right

要递归比较左子树的内测和右子树的内测 left->right vs right->left

只有当以上两个比较都返回true时候，才返回true

bool outside = cmp(left->left, right->right);
bool inside = cmp(left->right, right->left);
return ouside&&inside;

　　

完成代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool cmp(TreeNode * left, TreeNode * right){
    //递归函数
    if(left == NULL && right != NULL) return false;
    else if (left != NULL && right == NULL) return false;
    else if (left == NULL && right == NULL) return true;
    else if (left->val != right->val) return false;//这一条要放到下面，不然可能会出现子节点为空就读取val的错误

    //左右对称节点不空，val相等的情况
    bool outside = cmp(left->left, right->right);
    bool inside = cmp(left->right, right->left);
    return outside && inside;
    }

    bool isSymmetric(TreeNode* root) {
        if(root==NULL) return true;
        return cmp(root->left, root->right);
    }
};

“迭代逻辑”判断对称二叉树

使用队列来遍历二叉树，把对应的元素按特定的顺序放入队列。每次比较两个节点，看看相对应的节点是否相等

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if(root==NULL) return true;
        //队列存放比较节点
        queue<TreeNode*> que;
        que.push(root->left);
        que.push(root->right);
        while(!que.empty()){
            //把要比较的节点弹出来暂存 队列先进先出
            TreeNode * leftTemp = que.front();
            que.pop();
            TreeNode * rightTemp = que.front();
            que.pop();
            //当相对的两个节点都为空，则局部对称
            if(!leftTemp && !rightTemp) continue;
            //相对的两个节点一空一有值，或者是都不为空但是值不相等
            if(leftTemp&&!rightTemp || !leftTemp&&rightTemp || (leftTemp->val!=rightTemp->val)) return false;

            //因为上面两个if排除了为有空节点的情况，只剩下两个节点不为空，且值相等，所以push没毛病
            que.push(leftTemp->left);
            que.push(rightTemp->right);
            que.push(leftTemp->right);
            que.push(rightTemp->left);
        }
        return true;
    }
};

上面代码其实是把左右两个子树要比较的元素顺序放进一个容器，然后成对成对的取出来进行比较。那么除了队列，使用栈也可以啊，只要把容器替换一下，队列改为栈（因为成对成对弹出压入，不用改什么顺序）。

平衡二叉树

110. 平衡二叉树 - 力扣（LeetCode） (leetcode-cn.com)

给定一个二叉树，判断它是否是高度平衡的二叉树。本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

思路：重点是平衡怎么判断？左右子树的高度差绝对值小于等于1，既然是比较高度，递归+后序遍历就可以了：

递归函数的参数和返回值：返回的是当前节点的高度，参数为当前节点的指针

int getHeight(TreeNode * root){
      //递归函数  
}

终止条件：如果遇到空节点（叶子节点指向的NULL）,即返回 0

if(root == NULL) return 0;

单层递归逻辑: 先递归读取左子树高度，再递归读取右子树高度，相比较返回大的，并且差值如果大于等于2就不是平衡二叉树（但是因为是递归算法，不是很好直接退出函数返回，使用一个flag:-1 如果某一次的高度差大于1，那就是不平衡，一直影响到最后的输出）

int leftHeight = getHeight(root->left);
if(leftHeight==-1) return -1;

int rightHeight = getHeight(root->right);
if(rightHeight==-1) return -1;

return abs(leftHeight - rightHeight) > 1? -1 :max(leftHeight, rightHeight)+1;

　　

写出代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int getHeight(TreeNode* root){
        if(root == NULL) return 0;

        int leftHeight = getHeight(root->left);
        if(leftHeight==-1) return -1;
        int rightHeight = getHeight(root->right);
        if(rightHeight==-1) return -1;
        return abs(rightHeight-leftHeight) > 1? -1:max(rightHeight,leftHeight)+1;
    }
    bool isBalanced(TreeNode* root) {
        int heigh = getHeight(root);
        if(heigh==-1) return false;
        else return true;
    }
};

完全二叉树的节点个数

普通二叉树的节点个数

思路1，迭代法，统计每一层的节点个数，复杂度$O(n), O(n)$

class Solution {
public:
    int countNodes(TreeNode* root) {
        int res = 0;
        queue<TreeNode*> queueNode;
        if(root != NULL) queueNode.push(root);
        //空二叉树拳头警告
        while(!queueNode.empty()){
            //每次遍历一层，一层的节点在进入while时候确定，后面会改变，所以for循环中不能用size()，而应该用固定长度
            int layerSize = queueNode.size();
            res+=layerSize;
            vector<int> layerRes;
            for(int i =0;i<layerSize;i++){
                //先弹出队首元素，再check他的左右儿子
                TreeNode *tempNode = queueNode.front();
                queueNode.pop();
                layerRes.push_back(tempNode->val);
                if(tempNode->left) queueNode.push(tempNode->left);
                if(tempNode->right) queueNode.push(tempNode->right);
            }
            
        }
        return res;
    }
};

但是，看看AC之后的效率，内存消耗太大了，想办法提高空间复杂度O(n) -> O(\log(n))

思路2，递归法，复杂度$O(n), O(\log(n))$; 求节点个数，递归三部曲

函数参数和返回值：返回传入的节点作为根节点的子树有多少个节点，参数为当前节点

int countNodes(TreeNode* root){
     //递归函数  
}

终止条件：当root为NULL时，返回0

if(root==NULL) return 0;

单层递归逻辑

int leftNodes = get(root->left);
int rightNodes = get(root->right);
return leftNodes + rightNodes + 1;

　　

写出代码：

class Solution {
public:
    int count(TreeNode* root){
        if(root == NULL) return 0;
        return count(root->left) + count(root->right) + 1;
    }
    int countNodes(TreeNode* root) {
        return count(root);
    }
};

还可以简化

class Solution {
public:
    int countNodes(TreeNode* root) {
        if(root == NULL) return 0;
        return count(root->left) + count(root->right) + 1;
    }
};

完全二叉树的节点个数优化上面算法

222. 完全二叉树的节点个数 - 力扣（LeetCode） (leetcode-cn.com)

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：

在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 $1~ 2^h$ 个节点。p.s. 根节点为第0层

 那么，相对于普通二叉树，可以根据二叉树性质优化什么呢？

1. 如果是满二叉树，深度为k，那么节点个数为 $2^k-1$.
2. 如果是缺最后一层右侧节点的满二叉树，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照上面情况来计算。但如果不是满二叉树，就老老实实 $左+右+1$

即要么递归返回，要么使用满二叉树根据深度求节点返回（问题是既要返回节点个数又要求某个节点的深度）

求当前节点深度可以，根据满二叉树的性质和完全二叉树的性质，写如下代码：

int leftHeight = 0, rightHeight = 0; // 这里初始为0是有目的的，为了下面求指数方便
while (left) {  // 求左子树高度
    left = left->left;
    leftHeight++;
}
while (right) { // 求右子树高度
    right = right->right;
    rightHeight++;
}

• 时间复杂度：$O(\log n × \log n)$
• 空间复杂度：$O(\log n)$

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:

    int countNodes(TreeNode* root) {
        if(root == NULL) return 0;
        TreeNode* left = root->left;
        TreeNode* right = root->right;
        int leftHeight = 0, rightHeight = 0; // 这里初始为0是有目的的，为了下面求指数方便
        while (left) {  // 求左子树高度
            left = left->left;
            leftHeight++;
        }
        while (right) { // 求右子树高度
            right = right->right;
            rightHeight++;
        }
        if(leftHeight==rightHeight) return (2<<leftHeight)-1;



        return countNodes(root->left) + countNodes(root->right) + 1;
    }
};

二叉树的所有路径

257. 二叉树的所有路径 - 力扣（LeetCode） (leetcode-cn.com)

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

思路：递归（回溯）+前序遍历（为了方便父节点指向子节点）；

递归函数参数和返回值：记录路径，用string输出，所以参数为当前节点、记录路径的容器、记录输出的容器。

void catchPath(TreeNode* cur, vector<int>& path, vector<int>&res){
      //递归函数  
}

终止条件：当递归到叶子节点的时候就回溯

if(cur->left==NULL && cur->right==NULL){
    //终止逻辑  
}

具体的终止逻辑就是，当遇到叶子的时候，把当前路径加到res,

string tempPath;
for(int i=0;i<path.size()-1;i++){
     tempPath += to_string(path[i]);
     tempPath += "->";    
}
tempPath += to_string(path[path.size()-1]);
res.push_back(tempPath);
return;

　　

单层递归逻辑: 在哪里做回溯

递归完，为什么要做回溯？因为path 不能一直加入节点，它还要删节点，然后才能加入新的节点。一个递归对应一个回溯

if (cur->left) {
    catchPath(cur->left, path, res);
    path.pop_back(); // 回溯
}
if (cur->right) {
    catchPath(cur->right, path, res);
    path.pop_back(); // 回溯
}

　　

写出代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void catchPath(TreeNode* cur, vector<int>& path, vector<string>&res){
        //更新路径
        path.push_back(cur->val);
        //递归函数  
        if(cur->left==NULL && cur->right==NULL){
            //终止逻辑  
            string tempPath;
            for(int i=0;i<path.size()-1;i++){
                tempPath += to_string(path[i]);
                tempPath += "->";    
            }
            tempPath += to_string(path[path.size()-1]);
            res.push_back(tempPath);
            return;
        }  
        if (cur->left) {
            catchPath(cur->left, path, res);
            path.pop_back(); // 回溯
        }
        if (cur->right) {
            catchPath(cur->right, path, res);
            path.pop_back(); // 回溯
        } 
    }
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> res;
        vector<int> path;
        if (root == NULL) return res;
        catchPath(root,path,res);
        return res;
    }
};

左叶子之和

找树左下角的值

路径总和