近一段时间有个刚刚入行开发的朋友问我一些计数问题,
他说,它命名使用 toFixed() 方法来截取小数的长度了,虽然大部分都正常,但是有部分会出现结果不准确的问题。
先看图:
例如:

结果是:

但是:下面的就不是想要的结果了。


按道理结果应该是 82.1%的,但是实际上却不是这样。
先不说是什么原因导致的。
然后我让他改一下:变成:


就改变了一下运算位置,但是结果大不同。
到底哪一个才是正确的呢?我们来借助一下计算器:

结果已经很明显了,正确答案是 82.21%
我朋友他的想法是,先将5755 / 7000 然后得出的结果通过 toFixed() 方法 来截取3位小数,然后再乘以 100 来做一个百分百。
按道理来说,在平时的计算中这两个写法都是正确的才对啊,但是为什么会出现这样的情况呢?
先不要急,我们先来看一个最简单的例子:
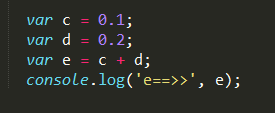
看到这里的时候你是不是第一时间觉得答案是 0.3 ?
那看一下js打印的结果是怎么样的。
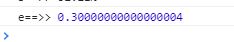
what?
0.1 + 0.2 竟然不是等于 0.3 ?
没错,这个就是 js 的计算问题了。所以上面出现答案不正确的问题就是因为js的计算方式导致的。
要弄清这个问题,首先我们需要了解的是:在计算机中数字是如何存储和运算的。
在计算机中,数字无论是整点数还是浮点数都是以多位二进制的方式进行存储的。
在JS中数字采用的IEEE 754的双精度标准进行存储,我们可以无需知道他的存储形式,
只需要简单的理解成就是存储一个数值所使用的二进制位数比较多而已,这样得到的数会更加精确。
这里为了简单直观,我们使用定点数来说明问题。在定点数中,如果我们以8位二进制来存储数字。
对于整数来说,十进制的35会被存储为: 00100011 其代表 2^5 + 2^1 + 2^0。
对于纯小数来说,十进制的0.375会被存储为: 0.011 其代表 1/2^2 + 1/2^3 = 1/4 + 1/8 = 0.375
而对于像0.1这样的数值用二进制表示你就会发现无法整除,最后算下来会是 0.000110011....由于存储空间有限,最后计算机会舍弃后面的数值,所以我们最后就只能得到一个近似值。
在JS中采用的IEEE 754的双精度标准也是一样的道理,我们且不管这个标准下的存储方式跟定点数存储有何不同,单单在这一点上他们都是相同的,也就是存储空间有限,
当出现这种无法整除的小数的时候就会取一个近似值,在js中如果这个近似值足够近似,那么js就会认为他就是那个值。
所以我们现在应该可以理解,就是说由于0.1转换成二进制时是无限循环的,所以在计算机中0.1只能存储成一个近似值。除了那些能表示成 x/2^n 的数可以被精确表示以外,其余小数都是以近似值得方式存在的。
在0.1 + 0.2这个式子中,0.1和0.2都是近似表示的,在他们相加的时候,两个近似值进行了计算,导致最后得到的值是0.30000000000000004,此时对于JS来说,
其不够近似于0.3,于是就出现了0.1 + 0.2 != 0.3 这个现象。 当然,也并非所有的近似值相加都得不到正确的结果。
有时两个近似值进行计算的时候,得到的值是在JS的近似范围内的,于是就可以得到正确答案。至于哪些值计算后能得到正确结果,哪些不能,我们也不需要去记。
最好的方法就是我们想办法规避掉这类小数计算时的精度问题就好了,那么最常用的方法就是将浮点数转化成整数计算。因为整数都是可以精确表示的。
所以,要解决类似问题,方法很简单,将浮点数转化成整数来计算就可以解决精度丢失问题了。