
协方差
对于变量X、Y,协方差的定义为每个时刻的“X值与其均值之差”乘以“Y值与其均值之差”的均值(其实是求“期望”)。因此,如果x与x的均值差与y与y的均值差的符号相同,则协方差值大于0,符号相反,则协方差值小于0,总结如下:
图2
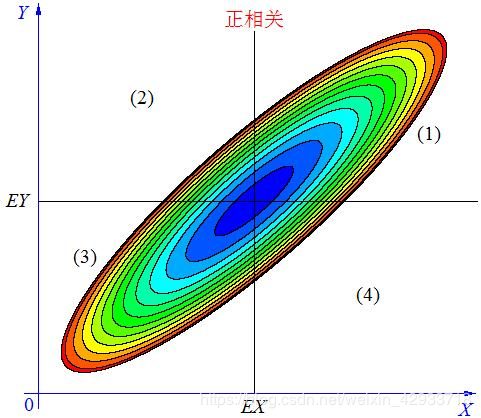
图3

图4
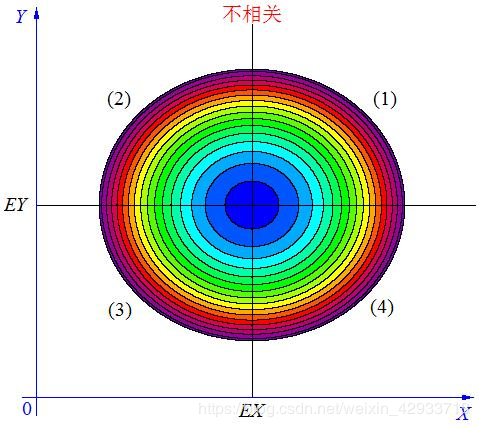
解释一:
X 越大 Y 也越大, X 越小 Y 也越小,这种情况,我们称为“正相关”。
X 越大Y 反而越小,X 越小 Y 反而越大,这种情况,我们称为“负相关”。
既不是X 越大Y 也越大,也不是 X 越大 Y 反而越小,这种情况我们称为“不相关”。
解释二:
在图2、3、4中的区域(1)中,有 X>EX ,Y-EY>0 ,所以(X-EX)(Y-EY)>0;
在图2、3、4中的区域(2)中,有 X<EX ,Y-EY>0 ,所以(X-EX)(Y-EY)<0;
在图2、3、4中的区域(3)中,有 X<EX ,Y-EY<0 ,所以(X-EX)(Y-EY)>0;
在图2、3、4中的区域(4)中,有 X>EX ,Y-EY<0 ,所以(X-EX)(Y-EY)<0。
当X 与Y 正相关时,它们的分布大部分在区域(1)和(3)中,小部分在区域(2)和(4)中,所以平均来说,有E(X-EX)(Y-EY)>0 。
当 X与 Y负相关时,它们的分布大部分在区域(2)和(4)中,小部分在区域(1)和(3)中,所以平均来说,有(X-EX)(Y-EY)<0 。
当 X与 Y不相关时,它们在区域(1)和(3)中的分布,与在区域(2)和(4)中的分布几乎一样多,所以平均来说,有(X-EX)(Y-EY)=0 。
所以,我们可以定义一个表示X, Y 相互关系的数字特征,也就是协方差
cov(X, Y) = E(X-EX)(Y-EY)。
当 cov(X, Y)>0时,表明 X与Y 正相关;
当 cov(X, Y)<0时,表明X与Y负相关;
当 cov(X, Y)=0时,表明X与Y不相关。
参考:https://blog.csdn.net/weixin_42933718/article/details/87983459