CF比赛题目地址:http://codeforces.com/contest/862
A. Mahmoud and Ehab and the MEX
·英文题,述大意:
输入n,x(n,x<=100),然后输入n个数作为一个集合。现在可以进行多次操作,每次操作为删除一个数或者添加一个数,求最少操作数使得集合Mex值等于x。
·分析:
也许是考察Mex的吧~那就当复习了,我们的策略是,如果当前集合的 Mex比x小,那就一直添加数;如果Mex比x大,那么就删除那个和x相同的元素就可以了。最后Mex==x输出0即可。
·代码:
1 #include"stdio.h"
2 #define go(i,a,b) for(int i=a;i<=b;i++)
3 int n,x,a,ans;bool exist[105];
4 int main()
5 {
6 scanf("%d%d",&n,&x);
7 go(i,1,n)scanf("%d",&a),exist[a]=1;
8 go(i,0,x-1)ans+=exist[i]^1;if(exist[x])ans++;printf("%d
",ans);return 0;
9 }//Paul_Guderian
B. Mahmoud and Ehab and the bipartiteness
·英文题,述大意:
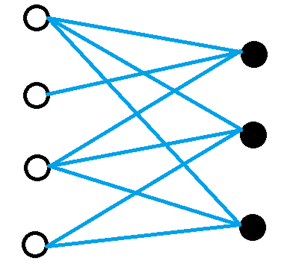
输入一个二分图,保证它是一个树(二分树……)。现在要使得原树变成完全二分图,求最多加入边数。完全二分图长这个样子:
·分析:
如上图,我们可以知道最后的总边数为:4*3(即两边点数相乘)。由于树的边数等于节点数减一,所以呢答案就是a*b-树边数(a,b分别为二分图两边的点数)。所以这道题清晰地告诉我们,它只需要一个二分图染色统计二分图两边的个数就可以了。
·呆呆的代码:
1 #include<stdio.h>
2 #define go(i,a,b) for(int i=a;i<=b;i++)
3 #define fo(i,a,x) for(int i=a[x],v=e[i].v;i;i=e[i].next,v=e[i].v)
4 const int N=100003;
5 struct E{int v,next;}e[N*2];int n,head[N],k=1,c[N],w;
6 void ADD(int u,int v){e[k]=(E){v,head[u]};head[u]=k++;}
7 void Dye(int u,int fa){fo(i,head,u)if(v!=fa)w+=(c[v]=3-c[u])==2,Dye(v,u);}
8 int main()
9 {
10 scanf("%d",&n);go(i,2,n){int u,v;scanf("%d%d",&u,&v);ADD(u,v);ADD(v,u);}
11 c[1]=1;Dye(1,1);printf("%I64d
",1ll*w*(n-w)-n+1);return 0;
12 }//Paul_Guderian
C. Mahmoud and Ehab and the xor
·英文题,述大意:
输入n,x(0<n<=105,0<=x<=105),表示现在需要我们构造一个含有n个不同元素的集合,并且满足:①元素为不大于106的非负整数②所有元素的异或结果等于x。如果可以构造,输出YES并且输出这个集合中的所有元素(按照任何顺序);如果不能,那么输出NO即可。
·分析:
看见这道题可能会纠结于怎样判断输出no还是yes的情况。但是事实上,根据异或的美妙(后文就会体现),仅有一种情况会输出no—n=2,x=0。
所以其他的都是Yes,那么怎么找出集合的n个元素呢?
我们知道异或的一个巧妙性质:0^任何数=0,偶数个相同的数抑或的结果为0。既然挨着挨着找每个元素很麻烦,那我们尝试使用这个性质,使得我们可以先胡乱取数异或出一个结果,然后再试图调整这个混乱的结果使它和x相等。
为什么会这样想?因为题目中有关键信息:元素大小不超过106,但是x是不超过105,意思说有一段区间x不存在。那么结合上文的胡乱思想,我们可以这样:现在已经将一些数异或起来了,答案是y。我们分情况讨论:
(1)x!=y:我们的目的是将y变回x,根据上文发现的异或性质,我们可以给y先抑或上一个y,再异或上一个x,就成为答案了!但是伤心的是,y万一已经用过了呢?这很难保证有没有用过。所以我们想到了可以找一个较大的数字,即在105~106的数字,因为它的二进制最高位是不会被改变的,由于选择的元素小于105所以在(105,106)之内选出的数是不会重复的,我们设这个很大的数字为a,那么我们将y依次异或上a和(a^x^y)这两个数,那不就既保证元素不重复,又保证异或结果为x了吗?OK。
(2)x==y:继续用上文的a和(a^x^y)不行了,因为x==y,那么这两个元素也是相同的。我们将其改成:a,a*2和(a^(a*2))这三个数,那么也可以满足条件。
最终的方法是:先将1~n-3的数异或起来的到y,然后:
如果x!=y:剩下三个元素为{0,a,a^x^y}
如果x==y:剩下三个元素为{a,a*2,a^(a*2)}
Over,呆码如下:
1 #include"stdio.h"
2 #define R return 0
3 #define go(i,a,b) for(int i=a;i<=b;i++)
4 int n,x,a=(1<<17),b=(1<<18),y;
5 int main()
6 {
7 scanf("%d%d",&n,&x);//QAQ
8 if(n==2&&!x){puts("NO");R;}puts("Yes");
9 if(n==1){printf("%d
",x);R;}
10 if(n==2){printf("%d %d
",0,x);R;}
11 go(i,1,n-3)y^=i,printf("%d ",i);x!=y?
12 printf("%d %d %d
",0,a,a^x^y):
13 printf("%d %d %d
",a,b,a^b);return 0;
14 }//Paul_Guderian
D. Mahmoud and Ehab and the binary string
·[题外话:那天晚上和圆盘盘全卡在C题,然后我果断去了D题,AC掉了从而保住了Rating]
·英文题,述大意:
这是一道交互题。输入n(n<=1000),表示这里有一个隐秘的长度为n的01串。现在你可以询问系统最多15次,询问内容为:输出一个长度为n的01串,然后系统会告诉你那个隐秘的串和你的这个串的汉明距离。最终你需要输出的答案,答案内容是输出任意一个0和1的下标(即输出两个下标,比如0100,你就输出1 2……)。
·分析:
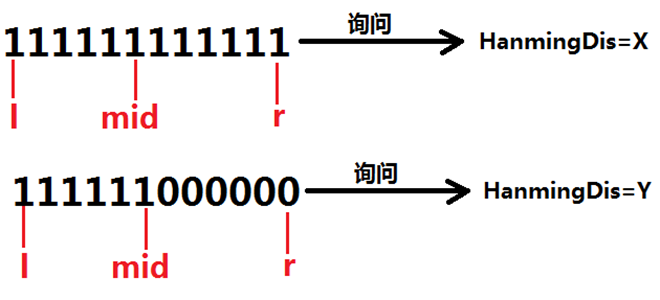
这样瞅瞅:n->1000,q->15有啥联系?至少我第一反应是:210=1024。因此我立下了用二分解决这道题的决心。初始情况下总要有一个串吧,所以可以初始化一个全为1的串。然后这样的结论可以高效解决问题:
·设右边半段长度为m,则有:
·如果X=Y+m,那么隐秘01串的右半段全是0;
·如果Y=X+m,那么隐秘01串的右半段全是1;
·若两种情况都不满足,那么:右半段必定同时含有01,我们就继续二分;
·因为答案在这里面都找得到,最终统计好了输出就是啦。
代码在这里:
1 #include<stdio.h>
2 #include<algorithm>
3 #define _ fflush(stdout)
4 #define go(i,a,b) for(int i=a;i<=b;i++)
5 int n,T=15,d,dis,_0,_1;char s[1003],t[1003];
6 void dfs(int l,int r)
7 {
8 if(l==r)
9 {
10 go(i,1,n)t[i]=s[i];t[l]='0';
11 putchar('?');putchar(' ');puts(t+1);_;
12 scanf("%d",&d);if(dis<d)_1=l;else _0=l;
13 }
14
15 if(_0&&_1){printf("! %d %d
",_0,_1);_;exit(0);}
16
17 int M=l+r>>1;go(i,1,n)t[i]=s[i];go(i,M+1,r)t[i]='0';
18 putchar('?');putchar(' ');puts(t+1);_;scanf("%d",&d);
19
20 if(d==dis-(r-M)){_0=r;dfs(l,M);return;}
21 if(d==dis+(r-M)){_1=r;dfs(l,M);return;}dfs(M+1,r);
22 }
23 int main()
24 {
25 scanf("%d",&n);go(i,1,n)s[i]='1';
26 putchar('?');putchar(' ');puts(s+1);_;
27 scanf("%d",&dis);dfs(1,n);return 0;
28 }//Paul_Guderian
我闻到初春的味道,那如同儿时梦境新鲜的芬芳;
也尝到思念的苦涩,这回望远方秋雨般无垠的萧索…——汪峰《无处安放》