这道题不就是简单的DP吗,BZOJ在水我!不,你是错的。
·本题特点:
不断向不同位置插入数字(按数字1,2,3,4,5,6……),需要求出每一次插入后的最长上升子序列。
·分析
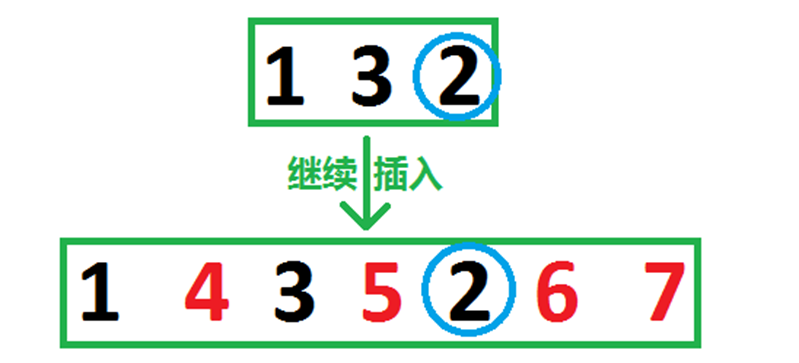
首先我们要着眼于“数字从小到大不断插入”这个行为的特点。如图:
我们设f[i]表示当前插入的数是i的时候(这道题特殊,i同样表示插入了i个数),那么我们发现,如果能够快速确定最终序列长什么样子,那么就可以按照读入(插入)顺序进行一次平凡的DP。
·一切都精确地指向这个序列最终的样子是什么这一问题。也就是说呀:我们需要一种高超的技术来维护区间插入操作。然后有人将两种方法分别称为“无脑”和“奇妙”。
[1]“无脑”数据结构——Treap
做了这题不经意间Treap就可以入门。Treap的特点是维护权值和优先级两个因素,这样的目的同时满足BST(可爱排序二叉树)和HEAP(堆)的性质,这样使得它可以维护序列的某种关键字下的排序(BST)和树的平衡(HEAP)。插入操作是Treap的基本玩法,但是插入要设法满足BST和HEAP的性质,也就是维护平衡和保证有序。维护平衡就是防止树的不当插入导致树退化成低级结构(最极端的是一条链,此时任何操作都是O(n)而不是O(logn)),维护平衡的方法就是旋转。旋转的特点是改变某些节点的父子关系以保证堆的性质,同时不会破坏维护的序列的排序(排序实际上就是树的中序遍历啦),对于一般的Treap,除了上述特点外,还会附带一个Maintain(大米饼常用Keep)函数来在旋转后维护节点信息(比如u的子树儿子节点个数等)。上述内容为Treap入门,然后使劲看代码搞懂Treap问题不大。
对于此题,我们的美妙Treap的排序权值是当前的插入位置,与其对应地,我们用SIZE[u]标记每一个子树的节点(表示一段区间内已插入的数的个数)。最后一旦我们拿到了最终序列,就自由了,你可以尽情的用任意优化方式进行一个nlongn的DP就可以啦(例如树状数组,zkw线段树,辅助数组二分法等)。
在数组版和指针版挣扎了一会,最终还是走上数组版Treap的道路。
大米饼习惯:ch[u][]表示左右儿子节点。一些基本操作在代码里很清晰。
1 #include<stdio.h> 2 #include<algorithm> 3 #define go(i,a,b) for(int i=a;i<=b;i++) 4 using namespace std;const int N=100010; 5 int n,v,ch[N][2],sz,P[N],siz[N],a[N],f[N],c[N],t,Re; 6 void Keep(int u){siz[u]=siz[ch[u][0]]+siz[ch[u][1]]+1;} 7 void ADD(int x,int d){while(x<=n)c[x]=max(c[x],d),x+=x&-x;} 8 void Get(int x){Re=0;while(x)Re=max(Re,c[x]),x-=x&-x;return;} 9 void Dfs(int u){if(!u)return;Dfs(ch[u][0]);a[++t]=u;Dfs(ch[u][1]);} 10 void Rotate(int &u,int d){ch[u][d]=ch[v=ch[u][d]][d^1];ch[v][d^1]=u;u=v;} 11 void Insert(int &u,int pos) 12 { 13 if(!u){siz[u=++sz]=1;P[u]=rand();return;} 14 int d=siz[ch[u][0]]<pos;siz[u]++; 15 Insert(ch[u][d],d?pos-1-siz[ch[u][0]]:pos); 16 if(P[u]<P[ch[u][d]])Rotate(u,d),Keep(ch[u][d^1]),Keep(u); 17 } 18 int main() 19 { 20 scanf("%d",&n);int _=0; 21 go(i,1,n)scanf("%d",&v),Insert(_,v);Dfs(_); 22 go(i,1,n)Get(a[i]),ADD(a[i],f[a[i]]=Re+1); 23 go(i,1,n)f[i]=max(f[i],f[i-1]),printf("%d ",f[i]); 24 return 0; 25 }//Paul_Guderian
跑出来800ms。然后就发现了接下来的方法,400ms。
[2]倒序构造法:对于构造最终序列,可以使用倒序的方法来反向模拟数的插入过程。可以理解我们现将所有数放进来,然后一个个拔出去。我们用一个数组表示:如果这个数还没有被拔出去,那么数组这一位为1,否则为0。如图:假设现在应该拔出a[i](即输入的:数字i插入到i位置上)
那么它在哪里?我们就在这个数组中查找第一个前缀和等于i的位置,那里就是它的真实位置(注意这里的i可以理解为第i个插入的),所以这一步我们使用二分法加一个维护前缀的东西就可以完成(偷懒就用个STL bound挺好的)。我们又一次的到了最终序列,然后就随意DP+优化就完成了。
在代码中,大米饼出于省空间和统一化等原因,直接用树状数组维护了前缀,自认为很方便呀!
(里面夹杂了一些读入优化输出优化)
1 #include<stdio.h> 2 #include<cstring> 3 #include<algorithm> 4 #define go(i,a,b) for(int i=a;i<=b;i++) 5 #define ro(i,a,b) for(int i=a;i>=b;i--) 6 using namespace std;const int N=100003; 7 int a[N],c[N],f[N],n,l,r,M,t; 8 inline void Add(int x,int d){while(x<=n)c[x]+=d,x+=x&-x;} 9 inline void Up(int x,int d){while(x<=n)c[x]=max(c[x],d),x+=x&-x;} 10 inline int Sum(int x){int res=0;while(x)res+=c[x],x-=x&-x;return res;} 11 inline int Max(int x){int M=0;while(x)M=max(M,c[x]),x-=x&-x;return M;} 12 inline void Nick(int x){if(x<0)putchar('-'),x=-x;if(x>9)Nick(x/10);putchar(x%10+'0');} 13 inline int Judy(int &x) 14 { 15 x=0;int w=1;char c=0; 16 while(c<'0'||c>'9'){if(c=='-')w=-1;c=getchar();} 17 while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar();x*=w;return 1; 18 } 19 int main() 20 { 21 Judy(n);go(i,1,n)Judy(a[i]),Add(i,1); 22 ro(i,n,1){l=1,r=n;while(l<r)M=l+r>>1,Sum(M)<a[i]+1?l=M+1:r=M;Add(a[i]=r,-1);} 23 go(i,1,n)Up(a[i],f[i]=Max(a[i])+1),f[i]=max(f[i],f[i-1]),Nick(f[i]),puts(""); 24 return 0; 25 }//Paul_Guderian
最后一个时间效率比较:
那天我见到他们在聚会上,
他们说那真是段糟糕的日子,
那不是他们想要的生活,
也许幸福是再次寻找在路上……——————汪峰《请把我在路上叫醒》