·英文题,述大意:
输入有向图一个(什么边的端点啊,边权啊)。每次可以选择一个节点和一个整数,然后把这个结点的出边边权加上该整数,入边边权减去该整数,目标:使得所有边的最小值非负且尽量大。
·分析:
修改结点周围的边权,题目中既没有限制次数,也没有规定在意先后顺序,这启示我们,每一个操作的效果是可以叠加的(同时就不分先后),所以可以将题目简化为:每一个节点只用一个整数操作一次。
差分约束的思想运用:如果我们设num(u)表示给节点u施加的那个整数值。则对于有向边(u,v)(权值为W),那么最终该边的边权为:
W'=W+num(u)-num(v)
读题目最后一句话,可以体会到这是一个美妙的二分。如果当前二分的值是X,表示最小边权。那么对于每一条边,都满足这个式子:
W+num(u)-num(v)>=X
=> num(v)-num(u)<=W-X
由于W-X在此时为定值,设P=W-X那么这些不等式都可以统一描述为:左边小于等于右边,左边两个节点信息之差,右边是一个定值。
扭一扭,泡一泡:那么原式为:num(v)<=num(u)+P
·然后这和最短路的if()中的东西是一样的,所以用这些元素依葫芦画瓢地建图(奥,这道题是帮你建好了的……)如果当前二分的X不符合条件,会出现什么情况————出现负环。
·为什么是出现负环就代表不能使所有不等式同时成立呢?
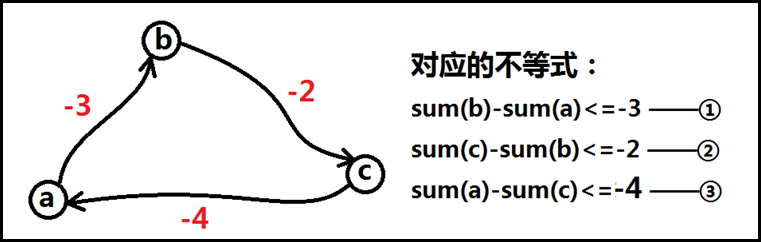
举例说明:(考虑一种建图状态)
如果将①③式相加,则会又得到一个关于b,c的不等式:
sum(c)-sum(b)>=7
该式子不幸地与②式矛盾。
总结归纳地说:只要一坨”连连不等式”(即图中一个环)右边的数值加起来的和为负数(这不是说每个值都是负数),那么对于任意其中点对{m,n},在原有的一个关于它们的不等式的基础上,可以通过其他等式相加再构造一个关于它俩的不等式中,必存在至少一组矛盾(一正一负,绝对爆炸)。所以负环就是不等式组不成立的直接表现。
·最后一个小提醒:在进行SPFA之前,该选谁作为起点呢?反正大家都是平等的,就一同压入队列吧。
1 #include<stdio.h>
2 #include<algorithm>
3 #include<queue>
4 #include<cstring>
5 #define go(i,a,b) for(int i=a;i<=b;i++)
6 #define fo(i,a,x) for(int i=a[x],v=e[i].v;~i;i=e[i].next,v=e[i].v)
7 #define inf 1000000000
8 #define mem(a,b) memset(a,b,sizeof(a))
9 using namespace std;const int N=503;struct E{int v,next,w;}e[N*80];
10 int n,m,head[N],k,max_W=-inf,ans,d[N],update_times[N];
11 void ADD(int u,int v,int w){e[k]=(E){v,head[u],w};head[u]=k++;}
12 bool SPFA(int x)
13 {
14 queue<int>q;bool inq[N]={0};
15 go(i,1,n)d[i]=update_times[i]=0,q.push(i),inq[i]=1;
16
17 while(!q.empty()){int u=q.front();q.pop();inq[u]=0;
18 fo(i,head,u)if(d[u]+e[i].w-x<d[v]){d[v]=d[u]+e[i].w-x;
19 if(!inq[v]){q.push(v);inq[v]=1;
20 if(++update_times[v]>n+1)return 0;}}}return 1;
21 }
22 int main(){while(~scanf("%d%d",&n,&m))
23 {
24 mem(head,-1);k=0;ans=-1;
25 go(i,1,m){int u,v,w;scanf("%d%d%d",&u,&v,&w);
26 max_W=max(max_W,w);ADD(u,v,w);}
27
28 int l=1,r=max_W+1,mid;
29 while(l<=r)mid=l+r>>1,SPFA(mid)?ans=mid,l=mid+1:r=mid-1;
30
31 if(ans==max_W+1){printf("Infinite
");continue;}
32 if(ans==-1){printf("No Solution
");continue;}
33 printf("%d
",ans);
34 }return 0;}//Paul_Guderian已经忘了回去的道路,走入独自一人的碎梦。————汪峰《碎梦》