- bzoj1074【Scoi2007】折纸
- 思路:考虑倒着做,每次将在折叠的直线右边的扔掉,左边的点再对称一次加入;
- 算几知识:求向量关于法向量的对称向量
- 点$A$关于点$B$对称的点$C = 2B - A$
- 如果要求$vec{A}$关于法向量$vec{l}$的对称向量$vec{A'}$;
- 可以考虑都平移到原点
- 利用点积求出$vec{A}$在$vec{l}$上的投影点$D$, 再将点$A$关于$D$对称到$A'$;
- $A'$的坐标就是向量$vec{A'}$
-
 bzoj1074
bzoj10741 #include<bits/stdc++.h> 2 #define db double 3 #define eps 1e-6 4 using namespace std; 5 const int N=1<<9; 6 int n,m,cnt,tmp; 7 int dcmp(db x){return fabs(x)<=eps?0:x<0?-1:1;} 8 struct point{ 9 db x,y; 10 point(db _x=0,db _y=0):x(_x),y(_y){}; 11 point operator +(const point&A)const{return point(x+A.x,y+A.y);} 12 point operator -(const point&A)const{return point(x-A.x,y-A.y);} 13 point operator *(const db&a)const{return point(x*a,y*a);} 14 db operator *(const point&A)const{return x*A.x+y*A.y;} 15 db operator ^(const point&A)const{return x*A.y-y*A.x;} 16 }p1[N],p2[N],q[N],qq[N]; 17 bool onleft(point A,point B,point C){ 18 return dcmp((C-B)^(A-B))>0; 19 } 20 point rev(point A,point B,point C){ 21 point D = C - B; 22 db l2 = D*D; 23 D = B + D*((A-B)*D/l2); 24 return D*2 - A; 25 } 26 int main(){ 27 #ifndef ONLINE_JUDGE 28 freopen("bzoj1074.in","r",stdin); 29 freopen("bzoj1074.out","w",stdout); 30 #endif 31 scanf("%d", &n); 32 for(int i=1;i<=n;i++)scanf("%lf%lf%lf%lf", &p1[i].x, &p1[i].y, &p2[i].x, &p2[i].y); 33 scanf("%d", &m); 34 for(int i=1;i<=m;i++){ 35 cnt=1;scanf("%lf%lf", &q[1].x, &q[1].y); 36 for(int j=n;j;j--){ 37 tmp=0; 38 for(int k=1;k<=cnt;k++)if(onleft(q[k],p1[j],p2[j])){ 39 qq[++tmp] = q[k]; 40 qq[++tmp] = rev(q[k],p1[j],p2[j]); 41 } 42 cnt=tmp; 43 if(!cnt)break; 44 for(int k=1;k<=cnt;k++)q[k]=qq[k]; 45 } 46 int ans=0; 47 // puts(""); 48 for(int j=1;j<=cnt;j++){ 49 // printf("%.2f %.2lf ",q[j].x, q[j].y); 50 if(dcmp(q[j].x)>0&&dcmp(q[j].y)>0&&dcmp(100-q[j].x)>0&&dcmp(100-q[j].y)>0){ 51 ans ++; 52 } 53 } 54 printf("%d ",ans); 55 } 56 return 0; 57 }
- bzoj1094【Zjoi207】粒子运动
- 思路:每个例子的路径是$k$段折线,枚举每对粒子和时间段计算最近距离;
- 算几知识:
- 1.求变化有的轨迹直接求出和圆的交点做出法向量求对称,对称的方法同上;
- 2.求圆和向量的交点(保证有交):
- 假设向量的起点$A$,方向$vec{B}$,圆C的圆心为$O$,半径为$R$
- 所以$( (A-O) + t vec{B} )^2 = R^2$
- 展开点积为常数,解二次方程即可;
-
 bzoj1094
bzoj10941 #include<bits/stdc++.h> 2 #define db double 3 #define il inline 4 using namespace std; 5 const int N=110; 6 int n,k; 7 db R,t[N][N]; 8 struct point{ 9 db x,y; 10 point(db _x=0,db _y=0):x(_x),y(_y){}; 11 point operator +(const point&A)const{return point(x+A.x,y+A.y);} 12 point operator -(const point&A)const{return point(x-A.x,y-A.y);} 13 point operator *(const db&a)const{return point(x*a,y*a);} 14 db operator *(const point&A)const{return x*A.x+y*A.y;} 15 db operator ^(const point&A)const{return x*A.y-y*A.x;} 16 }O,p[N][N],v[N][N]; 17 il db cal(db a,db b,db c){return ( -b + sqrt(b*b-4*a*c) ) / a / 2; } 18 il db len(point A){return sqrt(A*A);} 19 il db solve(int i,int j,int k1,int k2,db tl,db tr){ 20 point v1 = v[i][k1], v2 = v[j][k2]; 21 point p1 = p[i][k1] + v1 * (tl - t[i][k1]); 22 point p2 = p[j][k2] + v2 * (tl - t[j][k2]); 23 point tv = v1-v2, tp = p1-p2; tr-=tl; 24 db a=tv*tv,b=tv*tp*2,d=-b/a/2; 25 if(fabs(a)<1e-9)return b > 0 ? len(tv*tr+tp) : len(tv*tl+tp); 26 else { 27 d = max(0.0, min(tr, d)); 28 return len(tv*d+tp); 29 } 30 } 31 int main(){ 32 #ifndef ONLINE_JUDGE 33 freopen("bzoj1094.in", "r", stdin); 34 freopen("bzoj1094.out","w",stdout); 35 #endif 36 scanf("%lf%lf%lf",&O.x,&O.y,&R); 37 scanf("%d%d",&n,&k); 38 for(int i=1;i<=n;i++){ 39 scanf("%lf%lf%lf%lf",&p[i][0].x,&p[i][0].y,&v[i][0].x,&v[i][0].y); 40 for(int j=1;j<=k+1;j++){ 41 point tp = p[i][j-1] - O, tv = v[i][j-1]; 42 db tx = cal(tv*tv, tp*tv*2, tp*tp-R*R); 43 t[i][j] = t[i][j-1] + tx; 44 p[i][j] = p[i][j-1] + tv*tx; 45 point l = O - p[i][j]; swap(l.x,l.y),l.x=-l.x; 46 v[i][j] = l * ((tv*l)/(l*l)) * 2 - tv; 47 } 48 } 49 db ans = 1e18; 50 for(int i=1;i<=n;i++) 51 for(int j=1;j<=n;j++)if(i!=j){ 52 int k1=0,k2=0; 53 while(k1<=k&&k2<=k){ 54 ans = min(ans, solve(i, j, k1, k2, max(t[i][k1],t[j][k2]), min(t[i][k1+1],t[j][k2+1]))); 55 if(t[i][k1+1]<t[j][k2+1])k1++;else k2++; 56 } 57 } 58 printf("%.3lf ",ans); 59 return 0; 60 }
- bzoj1043【Hnoi2008】下落的圆盘
- 思路:枚举每个圆盘后面落下的圆盘,求相交的弧度区域,分别对每个圆求弧度并之后统计没有被覆盖的部分;
- 算几知识:
- 1.极角:
- 利用$atan2(y,x)$可以求得一个点的极角(弧度);
- 极角范围$(-pi,pi]$,大小逆时针(-x轴,-x轴]不断增大;
- x轴上半部分$+x$轴到$-x$轴不断增大,下半$-x$轴到$+x$轴不断增大;
- 特别注意的是:$+x$轴为$0$,$-x$为$pi$,$x$轴上方为正,下方为负,;
- 如果一个区间跨越了-x轴,那么需要分成两个区间处理;
- 2.求两圆交点及相交的极角弧度范围:
- 设小圆$O_{1}$半径$r_{1}$,大圆$O_{2}$半径$r_{2}$,圆心距$|O1O2| = d$,两个交点分别为$P_{1}$,$P_{2}$;
- 首先判断位置关系:$d > r_{1} + r_{2}$相离,$d < r_{2} - r_{1}$包含,都没有交点;
- (不考虑相切)然后:
- 在$ riangle O1O2P1$中用余弦定理算出$ angle P_{1}O_{1}O_{2}$,利用$vec{O_{1}O_{2}}$上下旋转调整可得$vec{O_{1}P_{1}} , vec{O_{1}P_{2}}$ ,由此可以算出$P_{1}P_{2}$
-
 bzoj1043
bzoj10431 #include<bits/stdc++.h> 2 #define db double 3 #define eps 1e-9 4 using namespace std; 5 const int N=1010; 6 const db pi = acos(-1); 7 int n,tot1[N],tot2[N],vis[N]; 8 db sub2[N][N<<2],cnt[N<<2]; 9 struct point{ 10 db x,y; 11 point(db _x=0,db _y=0):x(_x),y(_y){}; 12 point operator +(const point&A)const{return point(x+A.x,y+A.y);} 13 point operator -(const point&A)const{return point(x-A.x,y-A.y);} 14 db operator *(const point&A)const{return x*A.x+y*A.y;} 15 db operator ^(const point&A)const{return x*A.y-y*A.x;} 16 point operator *(const db&a)const{return point(x*a,y*a);} 17 }sub1[N][N<<2]; 18 struct circle{point o;db r;}c[N]; 19 int dcmp(db x){return fabs(x)<eps?0:x<0?-1:1;} 20 db len(point A){return sqrt(A*A);} 21 point rotate(point A,db cos,db sin){return point(A.x*cos-A.y*sin, A.y*cos+A.x*sin);} 22 void ins(int i,point p1,point p2){ 23 db l = atan2(p1.y,p1.x), r = atan2(p2.y,p2.x); 24 sub2[i][++tot2[i]] = l; 25 sub2[i][++tot2[i]] = r; 26 if(dcmp(l-r)>0){ 27 sub1[i][++tot1[i]]=point(-pi,r); 28 sub1[i][++tot1[i]]=point(l,pi); 29 }else sub1[i][++tot1[i]]=point(l,r); 30 } 31 void solve(int i,int j){ 32 if(dcmp(c[i].r-c[j].r)>0)swap(i,j); 33 point td = c[j].o - c[i].o,p0,p1,p2; 34 db d = len(td), r1=c[i].r, r2=c[j].r; 35 if(dcmp(d-r1-r2)>=0)return ; 36 if(dcmp(d-r2+r1)<=0){if(i<j)vis[i]=1;return ;} 37 db Cos = (td*td + r1*r1 - r2*r2) /d /r1 /2 ; 38 db Sin = sqrt(1-Cos*Cos); 39 p0 = td * (r1/d); 40 p1 = c[i].o + rotate(p0,Cos,-Sin);// 41 p2 = c[i].o + rotate(p0,Cos,Sin); 42 if(i<j)ins(i,p1-c[i].o, p2-c[i].o); 43 else ins(j,p2-c[j].o, p1-c[j].o); 44 } 45 int main(){ 46 freopen("bzoj1043.in","r",stdin); 47 freopen("bzoj1043.out","w",stdout); 48 scanf("%d",&n); 49 for(int i=1;i<=n;i++){ 50 scanf("%lf%lf%lf",&c[i].r,&c[i].o.x,&c[i].o.y); 51 for(int j=i-1;j;j--)solve(j,i); 52 } 53 db ans = 0; 54 for(int i=1;i<=n;i++){ 55 if(vis[i])continue; 56 sub2[i][++tot2[i]]=-pi; 57 sub2[i][++tot2[i]]=pi; 58 sort(sub2[i]+1,sub2[i]+tot2[i]+1); 59 for(int j=1;j<=tot2[i];j++)cnt[j]=0; 60 for(int j=1;j<=tot1[i];j++){ 61 int p1 = lower_bound(sub2[i]+1,sub2[i]+tot2[i]+1,sub1[i][j].x) - sub2[i]; 62 int p2 = lower_bound(sub2[i]+1,sub2[i]+tot2[i]+1,sub1[i][j].y) - sub2[i]; 63 cnt[p1]--,cnt[p2]++; 64 } 65 db all = 0; 66 for(int j=1;j<tot2[i];j++){ 67 cnt[j]+=cnt[j-1]; 68 if(!cnt[j])all += sub2[i][j+1]-sub2[i][j]; 69 } 70 ans += all * c[i].r; 71 } 72 printf("%.3lf ", ans); 73 }
- bzoj2433【Noi2011】智能车比赛
- 思路:处理相邻两个矩形的y坐标并$[l,r]$,可以通过的是这段,由于只会向右移动,所以利用斜率判断是否可走,直接dp即可;
- 也没有什么知识,注意使用到了斜率的话一定要注意在x坐标相同的特判,这题主要是s和t点的位置:
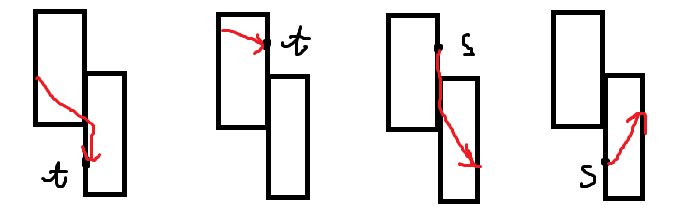
- 所以在同一x坐标上的[l,r]意义可能不同,特判s,t的位置再调整一下dp边界;
-
 bzoj2433
bzoj24331 #include<bits/stdc++.h> 2 #define inf 1e18 3 #define db double 4 #define eps 1e-8 5 using namespace std; 6 const int N=2010; 7 int n; 8 db f[N][2],pv,qx[N],qy1[N],qy2[N]; 9 int dcmp(db x){return fabs(x)<eps?0:x<0?-1:1;} 10 struct point{ 11 db x,y; 12 point(db _x=0,db _y=0):x(_x),y(_y){}; 13 }s,t,p[N][2]; 14 db calk(point x,point y){ 15 if(!dcmp(x.x-y.x))return dcmp(x.y-y.y)*inf; 16 return (y.y-x.y)/(y.x-x.x); 17 } 18 db dis(point x,point y){return sqrt((x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y));} 19 void relax(point&tp,int&pos,int typ){ 20 if(tp.x==qx[pos]){ 21 if(tp.y==p[pos][0].y)tp.y+=eps; 22 if(tp.y==p[pos][1].y)tp.y-=eps; 23 int tmp = typ>0?pos:pos-1; 24 if(dcmp(tp.y-qy1[tmp])>=0&&dcmp(tp.y-qy2[tmp])<=0)pos+=typ; 25 } 26 } 27 int main(){ 28 #ifndef ONLINE_JUDGE 29 //freopen("bzoj2433.in","r",stdin); 30 //freopen("bzoj2433.out","w",stdout); 31 #endif 32 scanf("%d",&n); 33 for(int i=1;i<=n;i++)scanf("%lf%lf%lf%lf",&qx[i],&qy1[i],&qx[i+1],&qy2[i]); 34 scanf("%lf%lf%lf%lf%lf",&s.x,&s.y,&t.x,&t.y,&pv); 35 if(s.x>t.x)swap(s,t); 36 qy1[0]=-inf,qy2[0]=inf; 37 for(int i=1;i<=n;i++){ 38 p[i][0] = point(qx[i],max(qy1[i],qy1[i-1])); 39 p[i][1] = point(qx[i],min(qy2[i],qy2[i-1])); 40 for(int j=0;j<2;j++)f[i][j]=inf; 41 } 42 int ps = lower_bound(qx+1,qx+n+1,s.x-eps)-qx; 43 int pt = lower_bound(qx+1,qx+n+1,t.x+eps)-qx-1; 44 db l,r,t1,t2; 45 relax(s,ps,1); 46 relax(t,pt,-1); 47 for(int i=ps;i<=pt;i++) 48 for(int j=0;j<2;j++){ 49 l=-inf,r=inf; 50 point now = p[i][j]; 51 for(int k=i-1;k>=ps;k--){ 52 l = max(l, t1=calk(now,p[k][1])); 53 r = min(r, t2=calk(now,p[k][0])); 54 if(dcmp(t2-l)>=0&&dcmp(t2-r)<=0){ 55 f[i][j] = min(f[i][j], f[k][0] + dis(now,p[k][0])); 56 } 57 if(dcmp(t1-l)>=0&&dcmp(t1-r)<=0){ 58 f[i][j] = min(f[i][j], f[k][1] + dis(now,p[k][1])); 59 } 60 } 61 t1=calk(s,now); 62 if(dcmp(t1-l)>=0&&dcmp(t1-r)<=0)f[i][j]=min(f[i][j],dis(s,now)); 63 } 64 db ans=inf; 65 l=-inf;r=inf; 66 for(int i=pt;i>=ps;i--){ 67 l=max(l,t1=calk(t,p[i][1])); 68 r=min(r,t2=calk(t,p[i][0])); 69 if(dcmp(t2-l)>=0&&dcmp(t2-r)<=0){ 70 ans = min(ans, f[i][0]+dis(p[i][0],t)); 71 } 72 if(dcmp(t1-l)>=0&&dcmp(t1-r)<=0){ 73 ans = min(ans, f[i][1]+dis(p[i][1],t)); 74 } 75 } 76 t1=calk(s,t); 77 if(dcmp(t1-l)>=0&&dcmp(t1-r)<=0){ 78 ans = min(ans,dis(s,t)); 79 } 80 ans /= pv; 81 printf("%.8lf ",ans); 82 return 0; 83 }
- bzoj2864战火星空
- 做网络流的时候做的,写下面了;
- https://www.cnblogs.com/Paul-Guderian/p/10128831.html
- 算几知识:求圆和一条直线的交点;
- 先求出垂足,在用勾股定理算出底边长,向量加减可得两个交点;
-
 bzoj2864
bzoj28641 #include<bits/stdc++.h> 2 #define inf 1e18 3 #define ld long double 4 #define eps 1e-9 5 using namespace std; 6 const int N=400010; 7 struct point{ 8 ld x,y; 9 point(ld _x=0,ld _y=0):x(_x),y(_y){}; 10 point operator +(const point&A){return point(x+A.x,y+A.y);} 11 point operator -(const point&A){return point(x-A.x,y-A.y);} 12 point operator *(const ld&A){return point(x*A,y*A);} 13 ld operator ^(const point&A){return x*A.y-y*A.x;} 14 ld operator *(const point&A){return x*A.x+y*A.y;} 15 }A[21]; 16 struct line{point s,t;ld v,r,e;}B[21]; 17 int T,n,m,tot,o,hd[N],cur[N],vis[N],dis[N]; 18 ld s[21][21],t[21][21],sub[N]; 19 struct Edge{int v,nt; ld f;}E[N<<1]; 20 queue<int>q; 21 int dcmp(ld x){return fabs(x)<eps?0:x<0?-1:1;} 22 point cross(point P,point v,point Q,point w){ 23 point u=P-Q; 24 ld tmp=(w^u)/(v^w); 25 return P+v*tmp; 26 } 27 void cal(int i,int j){ 28 point P,Q,C,v,w; ld d,dt,t0,t1,t2,tl,tr; 29 P=A[i];Q=B[j].s; 30 w=B[j].t-B[j].s; 31 v=point(-w.y,w.x); 32 C=cross(P,v,Q,w); 33 v=C-P; 34 d=(B[j].r*B[j].r)-(v*v); 35 if(dcmp(d)<0)return; 36 d=sqrt(d); 37 dt=d/B[j].v; 38 tl=0;tr=sqrt(w*w)/B[j].v; 39 v=C-Q; 40 if(dcmp(v.x*w.x)>0)t0=sqrt(v*v)/B[j].v; 41 else t0=-sqrt(v*v)/B[j].v; 42 t1=t0-dt,t2=t0+dt; 43 s[i][j]=max(t1,tl); 44 t[i][j]=min(t2,tr); 45 if(dcmp(s[i][j]-t[i][j])<0){ 46 sub[++tot]=s[i][j]; 47 sub[++tot]=t[i][j]; 48 } 49 } 50 void adde(int u,int v,ld f){ 51 // printf("%d %d %Lf ",u,v,f); 52 E[o]=(Edge){v,hd[u],f};hd[u]=o++; 53 E[o]=(Edge){u,hd[v],0};hd[v]=o++; 54 } 55 bool in(ld s1,ld t1,ld s2,ld t2){return dcmp(s1-s2)<=0&&dcmp(t1-t2)>=0;} 56 bool bfs(){ 57 for(int i=0;i<=T;i++)vis[i]=dis[i]=0; 58 vis[0]=dis[0]=1;q.push(0); 59 while(!q.empty()){ 60 int u=q.front();q.pop(); 61 for(int i=hd[u],v;~i;i=E[i].nt)if(dcmp(E[i].f)>0){ 62 if(!vis[v=E[i].v])vis[v]=1,q.push(v),dis[v]=dis[u]+1; 63 } 64 } 65 return vis[T]; 66 } 67 ld dfs(int u,ld F){ 68 if(u==T||!dcmp(F))return F; 69 ld flow=0,f; 70 for(int i=cur[u];~i;i=E[i].nt){ 71 int v=E[cur[u]=i].v; 72 if(dis[v]==dis[u]+1&&dcmp(f=dfs(v,min(F,E[i].f)))>0){ 73 flow+=f,F-=f; 74 E[i].f-=f,E[i^1].f+=f; 75 if(!dcmp(F))break; 76 } 77 } 78 return flow; 79 } 80 ld dinic(){ 81 ld flow=0; 82 while(bfs()){ 83 for(int i=0;i<=T;i++)cur[i]=hd[i]; 84 flow+=dfs(0,inf); 85 } 86 return flow; 87 } 88 int main(){ 89 freopen("bzoj2864.in","r",stdin); 90 freopen("bzoj2864.out","w",stdout); 91 memset(hd,-1,sizeof(hd)); 92 scanf("%d%d",&n,&m); 93 for(int i=1;i<=n;i++)scanf("%Lf%Lf",&A[i].x,&A[i].y); 94 for(int i=1;i<=m;i++){ 95 scanf("%Lf%Lf%Lf%Lf",&B[i].s.x,&B[i].s.y,&B[i].t.x,&B[i].t.y); 96 scanf("%Lf%Lf%Lf",&B[i].v,&B[i].r,&B[i].e); 97 } 98 for(int i=1;i<=n;i++) 99 for(int j=1;j<=m;j++){ 100 cal(i,j); 101 } 102 sort(sub+1,sub+tot+1); 103 if(tot)tot--;T=tot*n+m+1; 104 for(int i=1;i<=m;i++)adde(0,i,B[i].e); 105 for(int i=1;i<=tot;i++) 106 for(int j=1;j<=n;j++){ 107 adde((i-1)*n+j+m,T,sub[i+1]-sub[i]); 108 } 109 /* 110 for(int i=1;i<=tot;i++)printf("%.6Lf ",sub[i]); 111 puts(""); 112 */ 113 /* 114 for(int i=1;i<=n;i++) 115 for(int j=1;j<=m;j++){ 116 printf("%.6Lf %.6Lf %6Lf ",s[i][j],t[i][j],t[i][j]-s[i][j]); 117 }*/ 118 for(int i=1;i<=n;i++) 119 for(int j=1;j<=m;j++) 120 for(int k=1;k<=tot;k++)if(in(s[i][j],t[i][j],sub[k],sub[k+1])){ 121 ld tmp=t[i][j]-s[i][j]; 122 if(dcmp(tmp)>0)adde(j,(k-1)*n+m+i,inf); 123 } 124 ld ans = dinic(); 125 printf("%.6Lf ",ans); 126 return 0; 127 }
- bzoj2458【Beijing2011】最小三角形
- 平面最近点对:
- https://www.luogu.org/blog/user277/solution-p1429
- 这题依旧求解分治:
- 先按照$x$排序,以$L = p[mid].x$为轴划分,求解$[l,mid]$和$[mid+1,r]$,假设现在的最小答案为$ans$;
- 需要计算跨越两边的答案;
- 根据三角形边的关系,顶点间的距离不会超过$frac{ans}{2}$;
- 所以我们可以对每个点维护一个$d*2d$的矩形;
- 具体每次按$y$归并,将$L$沿x轴左右$ans/2$的点都加进来,双指针扫描维护$y$;
- 由于不能比答案更小,在每个$d*2d$的矩形内的点的个数大约为$O(1)$
- 这样就是$n log n$
- 注意双指针的维护不能取$abs$
-
 bzoj2458
bzoj24581 #include<bits/stdc++.h> 2 #define db long double 3 using namespace std; 4 const int N=200010; 5 int n; 6 db ans=1e18; 7 struct point{ 8 db x,y; 9 bool operator <(const point&A)const{return x<A.x;} 10 }p[N],pl[N],pr[N],tmp[N]; 11 db dis(point A,point B){return sqrt((A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y));} 12 void solve(int l,int r){ 13 if(l==r){return;} 14 int mid=(l+r)>>1; 15 db txl=p[mid].x,txr=p[mid].x; 16 solve(l,mid);solve(mid+1,r); 17 int totl=0,totr=0; 18 db mx = ans/2; 19 for(int i=l;i<=mid;i++)if(txl-p[i].x<=mx)pl[++totl]=p[i]; 20 for(int i=mid+1;i<=r;i++)if(p[i].x-txr<=mx)pr[++totr]=p[i]; 21 for(int i=1,t1=1,t2=0;i<=totl;i++){ 22 while(t1<=totr&&/*abs*/pl[i].y-pr[t1].y/*)*/>mx)t1++; 23 while(t2<totr&&/*abs*/pr[t2+1].y-pl[i].y/*)*/<=mx)t2++; 24 for(int j=t1;j<=t2;j++) 25 for(int k=j+1;k<=t2;k++){ 26 ans = min(ans, dis(pl[i],pr[j]) + dis(pl[i],pr[k]) + dis(pr[j],pr[k])); 27 } 28 } 29 for(int i=1,t1=1,t2=0;i<=totr;i++){ 30 while(t1<=totl&&/*abs(*/pr[i].y-pl[t1].y/*)*/>mx)t1++; 31 while(t2<totl&&/*abs(*/pl[t2+1].y-pr[i].y/*)*/<=mx)t2++; 32 for(int j=t1;j<=t2;j++) 33 for(int k=j+1;k<=t2;k++){ 34 ans = min(ans, dis(pr[i],pl[j]) + dis(pr[i],pl[k]) + dis(pl[j],pl[k])); 35 } 36 } 37 int t=l,j=mid+1; 38 for(int i=l;i<=mid;i++){ 39 while(j<=r&&p[j].y<p[i].y)tmp[t++]=p[j++]; 40 tmp[t++]=p[i]; 41 } 42 for(;j<=r;j++)tmp[t++]=p[j]; 43 for(int i=l;i<=r;i++)p[i]=tmp[i]; 44 } 45 int main(){ 46 #ifndef ONLINE_JUDGE 47 // freopen("bzoj2458.in","r",stdin); 48 // freopen("bzoj2458.out","w",stdout); 49 #endif 50 scanf("%d",&n); 51 for(int i=1;i<=n;i++)scanf("%Lf%Lf",&p[i].x,&p[i].y); 52 sort(p+1,p+n+1); 53 solve(1,n); 54 printf("%.6Lf ",ans); 55 return 0; 56 }
