由于两种线段要交替出现,有解的必要条件即为$h=v$(以下均记为$n$)
进一步的,再假设两种线段依次对应于向量$(a_{i},0)$和$(0,b_{i})$,根据题意要求向量长度为给定值且和为0,那么也即有$|a_{i}|=l_{i},|b_{i}|=p_{i}$且$sum_{i=1}^{n}a_{i}=sum_{i=1}^{n}b_{i}=0$
使用背包判定是否存在这样的$a_{i}$和$b_{i}$,若不存在即无解,若存在则再求出任意一组
(可以证明此时一定有解,以下即为构造)
若$a_{i}$中的负数少于$b_{i}$则将两者全部取相反数,再将两者分别从大到小排序(其实只需要保证正数在负数前),最后将$(a_{i},b_{i})$作为一个整体极角排序,并依次选择$(a_{1},0),(0,b_{1}),(a_{2},0),...,(b_{n},0)$即可
(代码实现上通过将两边分别合理排序使得其已经极角排序)
不难发现,以此法最终方案一定是形如下图的形式,即合法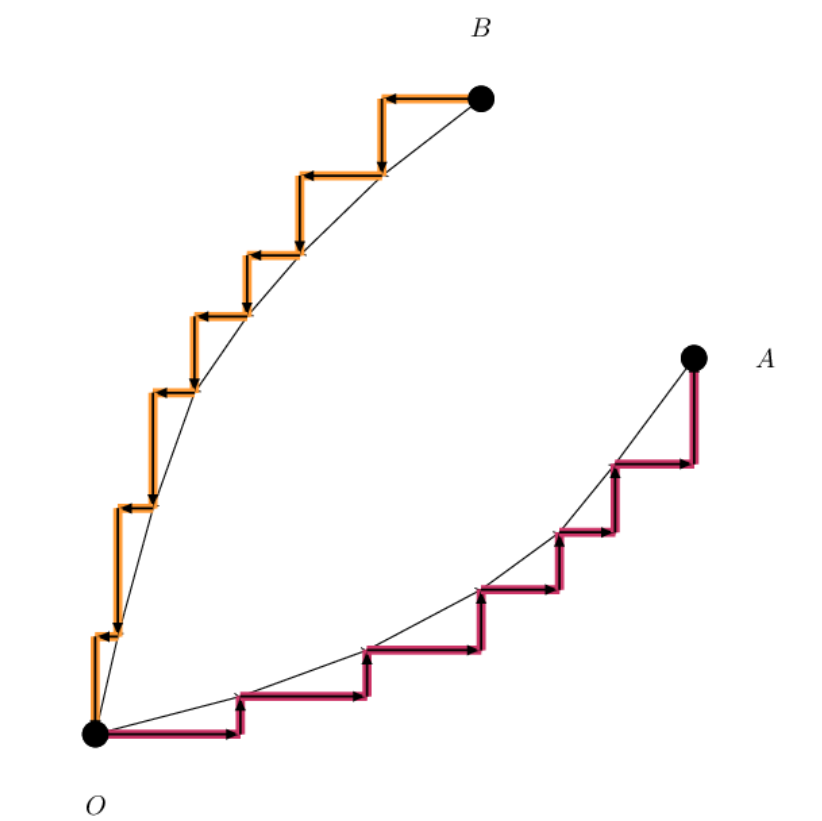
时间复杂度为$o(frac{nC^{2}}{omega})$,可以通过

1 #include<bits/stdc++.h> 2 using namespace std; 3 #define N 1005 4 bitset<N*N>f[N]; 5 int t,n,m,a[N],b[N]; 6 int calc(int *a){ 7 int m=0; 8 for(int i=1;i<=n;i++)m+=a[i]; 9 if (m&1)return 0; 10 m>>=1; 11 for(int i=1;i<=n;i++)f[i]=((f[i-1])|(f[i-1]<<a[i])); 12 if (!f[n][m])return 0; 13 for(int i=n;i;i--) 14 if (!f[i-1][m]){ 15 m-=a[i]; 16 a[i]=-a[i]; 17 } 18 return 1; 19 } 20 int main(){ 21 f[0][0]=1; 22 scanf("%d",&t); 23 while (t--){ 24 scanf("%d",&n); 25 for(int i=1;i<=n;i++)scanf("%d",&a[i]); 26 scanf("%d",&m); 27 for(int i=1;i<=m;i++)scanf("%d",&b[i]); 28 if ((n!=m)||(!calc(a))||(!calc(b))){ 29 printf("No "); 30 continue; 31 } 32 int cnt=0; 33 for(int i=1;i<=n;i++)cnt+=(a[i]<0)-(b[i]<0); 34 if (cnt<0){ 35 for(int i=1;i<=n;i++)a[i]=-a[i],b[i]=-b[i]; 36 } 37 sort(a+1,a+n+1),reverse(a+1,a+n+1); 38 sort(b+1,b+n+1),reverse(b+1,b+n+1); 39 for(int i=1;i<=n+1;i++) 40 if ((i>n)||(a[i]<0)){ 41 reverse(b+1,b+i); 42 break; 43 } 44 for(int i=n;i>=0;i--) 45 if ((!i)||(b[i]>0)){ 46 reverse(a+i+1,a+n+1); 47 break; 48 } 49 printf("Yes "); 50 for(int i=1,x=0,y=0;i<=n;i++){ 51 x+=a[i],printf("%d %d ",x,y); 52 y+=b[i],printf("%d %d ",x,y); 53 } 54 } 55 return 0; 56 }
