20172303 2018-2019-1《程序设计与数据结构》第9周学习总结
教材学习内容总结
常见的非线性结构有两种——树和图,在经过了三周对树的学习之后,本周我们接触了另一种非线性结构图的相关内容,包括图的概念、图的分类、图的实现方法等。
一、图的概述
- 概念:树中的每个结点都只有一个父结点,如果我们允许一个结点连通多个其他结点,树就变成了图。
- 相关术语:
- 顶点(Vertex):图中的数据元素。
- 边(Edge):图中各个顶点之间的连接。
- 邻接/邻居:两个顶点之间有一条边,则称这两个顶点是邻接的。
- 路径:连接两个顶点之间的一系列边称为两个顶点间的路径,边的条数称为路径长度(路径长度=顶点数-1)。
- 环路:首顶点与末顶点相同且路径中没有边重复的路径。
- 例:
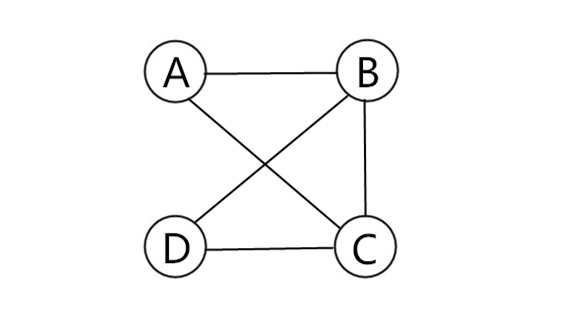
- 顶点:A,B,C,D
- 边:(A,B)(A,C)(B,C)(B,D)(C,D)
- 邻接:A与B是邻接结点,A与D不是邻接结点
- 路径:A→D——(A,B)(B,C)(C,D) 路径长度为3
- 环路:A→A——(A,B)(B,C)(C,A)
- 分类:
- 【是否有方向】无向图和有向图
- 【每条边带有权重或代价】加权图/网络(加权图可以是有向的也可以是无向的)
- 【特殊的图】生成树
1.无向图
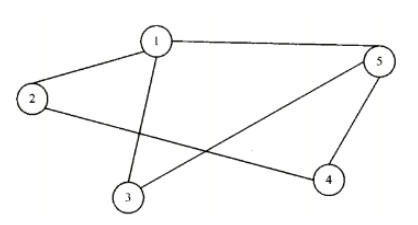
- 无向图是一种边为无序结点对的图。在无向图中,(A,B)(B,A)指的是一条边,表示A与B之间有一条两个方向都连通的边。
- 完全:一个无向图是完全的,说明对于有n个顶点的无向图,图中有n(n-1)/2条边。
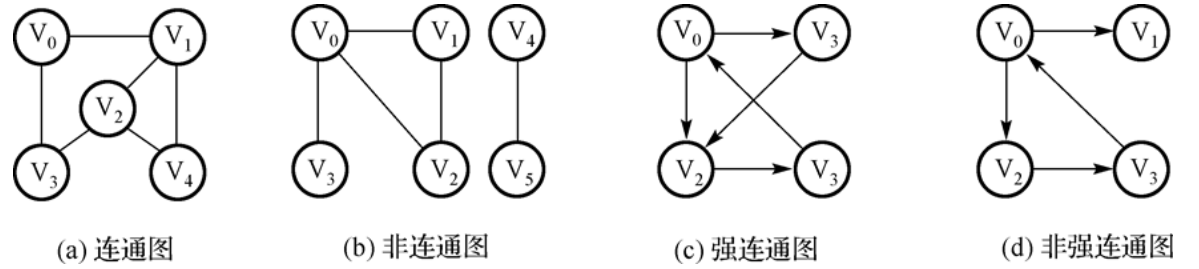
- 连通:如果无向图中的任何两个顶点之间都存在一条路径,则认为该无向图是连通的。
- 同时连通还分为强连通和弱连通(非强连通),强连通图中,任何两个顶点之间都是连通的,就是说任何两个顶点之间都至少有一条路径。
- 完全图一定是连通图,连通图不一定是完全图。
- 无向树:一种连通的没有环路的,其中一个元素被指定为树根的图。
2.有向图
- 有向图/双向图是一种边为有序顶点对的图。在无向图中,(A,B)(B,A)指的不是一条边,(A,B)表示从A到B有一条连通的边,但B到A没有。
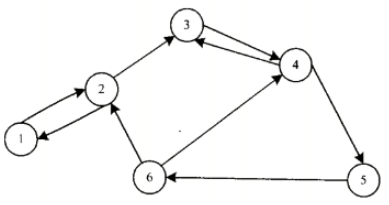
- 拓扑序:书上的说法是:“如果有向图中没有环路,且有一条从A到B的边,则可以把顶点A安排在顶点B之前,这种排列得到的顶点次序称为拓扑序”。说实话我看了七八遍也没看懂这句话说的是什么意思,后来上百度搜了一下,有了下面这张图就很好理解了。
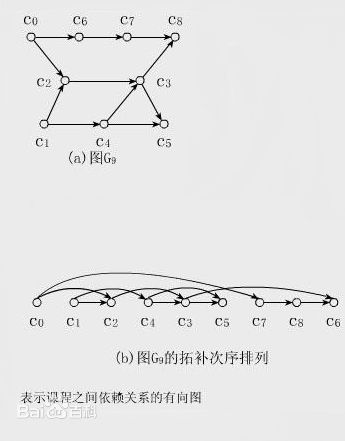
- 有向树:其中一个元素被指定为树根的有向图称为有向树。
3.加权图
- 加权图/网络:是一种每条边都带有权重或代价的图。加权图中,某一条路径的权重等于该路径中所有边权重的总和。
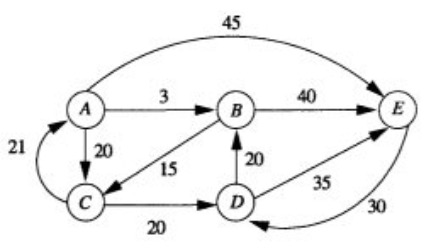
- 加权图中边的表示:在普通的图中,我们表示边时只需要起始顶点和终止顶点即可,但是在加权图中,除了上面的两项外还需要增加一个表示权重的元素。例如在有向图中,从A到B之间有一条边,权重为3,那么它的表示就为(A,B,3)
4.生成树
- 概念:一颗含有图中所有顶点和部分边的树。一个图的生成树不一定是唯一的。
- 最小/大生成树:树中的路径权重总和小于/大于它所来源的图中的任何一颗生成树的权重总和。
二、图的算法
(一)遍历
- 图的遍历分为两种:广度优先遍历(简称BFS,与树中的层序遍历类似)深度优先遍历(简称DFS,与树中的前序遍历类似)。
- 广度优先遍历——使用一个队列和一个无序列表来实现,队列用于管理遍历,无序列表用于存储遍历结果。
- 第一步:起始顶点进入队列,标记为已访问。
- 第二步:从队列中取出起始顶点加入无序列表的末端,让与该顶点相连的还未被标记为已访问的顶点加入队列中,把它们都标记为已访问。
- 第三步:重复第二步的操作,每次取出队列中的首个顶点加入无序列表,直至队列为空。
- 深度优先遍历——使用一个栈和一个无序列表来实现,栈的作用与广度优先遍历中队列的作用相同。
- 第一步:起始顶点进入栈。
- 第二步:从栈中取出起始顶点加入无序列表的末端,标记为已访问,让与该顶点相连的顶点加入栈中。
- 第三步:重复第二步的操作,每次取出栈顶元素加入无序列表,把顶点标记为已访问,直至栈为空。
- 实例
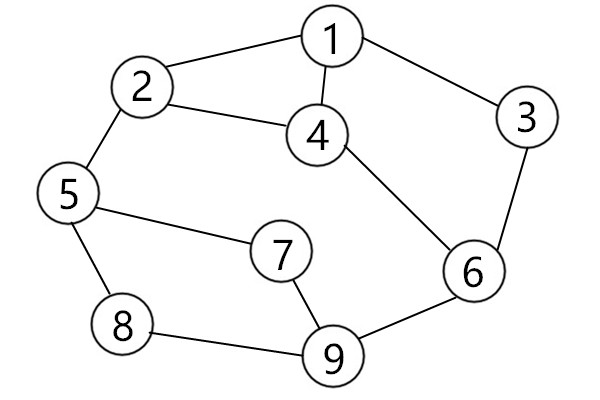
- 广度优先遍历:9、6、7、8、3、4、5、1、2
- 过程:
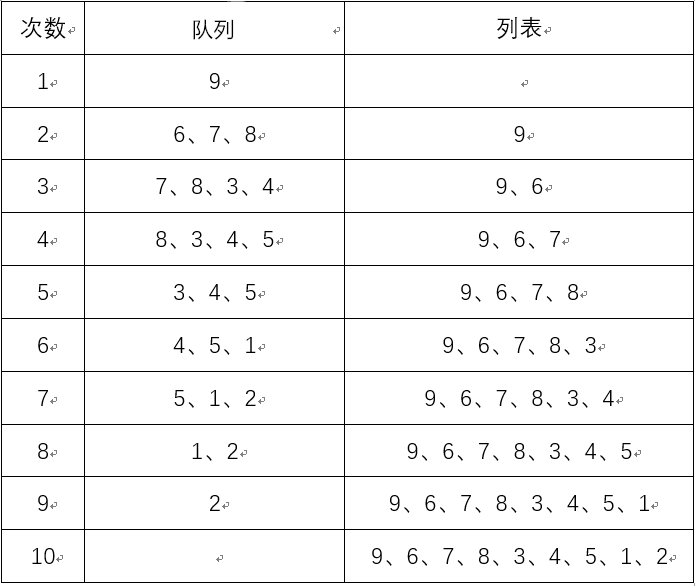
- 过程:
- 深度优先遍历:9、6、3、1、2、4、5、7、8
- 过程:
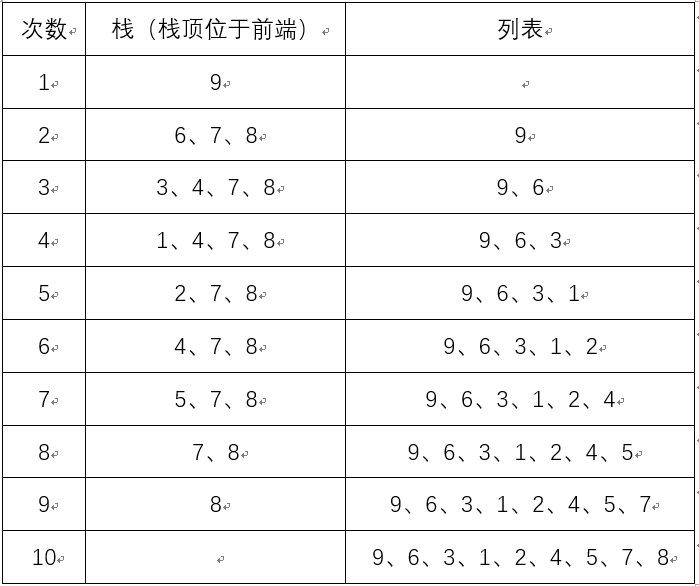
- 过程:
- 广度优先遍历:9、6、7、8、3、4、5、1、2
(二)测试连通性
- 要判断一个图的连通性,需要确定图中的任意两个顶点之间都有一条路径,如果直接判断的话时间复杂度会很大。书上给出了一种简单的判断方法:在一个含n个顶点的图中,当且仅当图中的每个顶点的广度优先遍历的无序列表长度都为n时,证明该图就是连通的。
(三)最小生成树
- 推衍算法(以最小生成树为例):在寻找最小树的过程中需要一个最小堆用于每次寻找最小边
- (1)从图中任选一个起始顶点,将它添加到最下生成树中
- (2)将所有含起始顶点的边按照权重由小到大的顺序加入到最小堆中
- (3)从最小堆中选出权重最小的边,将该边和与该边连接的最小生成树中没有的顶点加入最小生成树中,加入的顶点成为新的起始顶点。
- (4)重复第二和第三步直至最小生成树中含有图的所有顶点或最小堆为空时。
(四)判断最短路径
- 情况一:最短路径为两个顶点之间的最小边数
- 这种情况下将广度优先遍历进行修改即可实现,修改方式为在遍历的过程中增加两个信息:从起始顶点到遍历到该顶点的路径长度(为了便于计算最短路径长度),以及路径中该顶点的前驱结点((为了便于输出整条最短路径)。
- 情况二:最短路径为加权图中路径权重总和最小的路径
- 这种情况下仍然是对广度优先遍历进行修改即可。首先,把顶点队列改为最小堆或优先队列,这样在存储顶点时就可以依据起始顶点到被存储顶点的权重和的大小顺序来进行存储。和情况一一样,在遍历过程中需要增加两个信息:一是从起始顶点开始到所遍历顶点的最小路径权重,而是路径上该顶点的前驱。
三、图的实现策略
(一)邻接列表
- 邻接列表是一种特殊的链表,它的图样类似于哈希排序中的链地址法,顶点存储在一个列表中,每个顶点又拥有一个边列表。对于无向图而言,一条边会同时出现在边两边的两个顶点的邻接列表中。对于加权图而言,每条边还会存储一个值代表该边的权重。
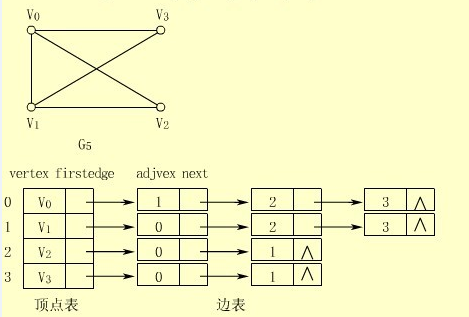
(二)邻接矩阵
- 邻接矩阵是表示图形中顶点之间相邻关系的矩阵,对于n个顶点的图而言,该图的邻接矩阵有n行n列,每一个(行,列)或(列,行)代表了两个顶点之间的一条边。对于无向图,如果A1和A2之间有一条边,那么在二维矩阵中,matrix[A1,A2]和matrix[A2,A1]处的值为1。对于有向图,如果A1和A2之间有一条A1指向A2的边,那么matrix[A1,A2]处的值为1,matrix[A2,A1]处的值为0。对于加权图,把相应位置的1换成权值即可。
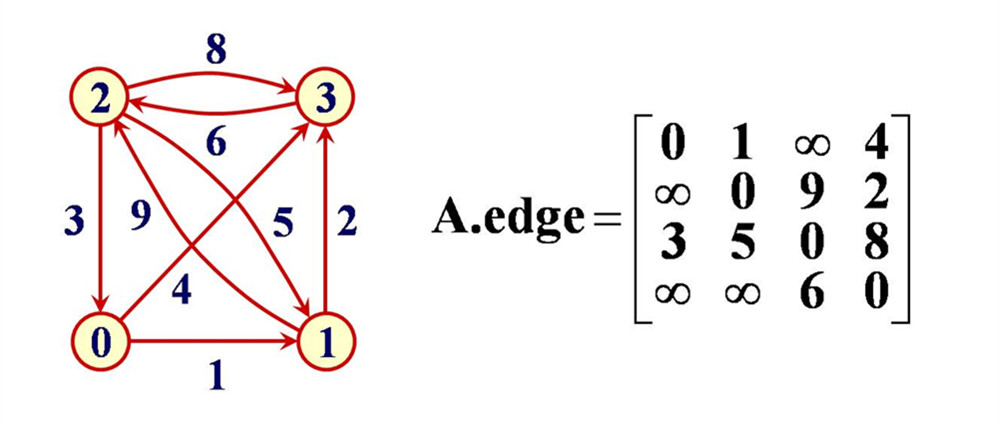
- 用邻接矩阵实现无向图
- 构造函数:构造函数中指数把图中的顶点数目设置为0,同时构建一个邻接矩阵和一个存储顶点的泛型数组。
protected final int DEFAULT_CAPACITY = 5; protected int numVertices; // 顶点数目 protected boolean[][] adjMatrix; // 布尔值的矩阵,存储顶点之间有无边 protected T[] vertices; // 存储顶点及顶点的value protected int modCount; public Graph() { numVertices = 0; this.adjMatrix = new boolean[DEFAULT_CAPACITY][DEFAULT_CAPACITY]; this.vertices = (T[])(new Object[DEFAULT_CAPACITY]); }addEdge方法:此方法用于在顶点之间添加边,添加的方法有两种,一种方法要输入的参数是两个顶点,另一种方法要输入的参数是两个顶点在邻接矩阵中的索引值。
public void addEdge(int index1, int index2) { if (indexIsValid(index1) && indexIsValid(index2)) { adjMatrix[index1][index2] = true; adjMatrix[index2][index1] = true; modCount++; } } // 使用顶点进行添加的方法实质上和上面用索引值添加的方法是一样的,只不过它使用了一个getIndex方法来获取顶点的索引值 public void addEdge(T vertex1, T vertex2) { addEdge(getIndex(vertex1), getIndex(vertex2)); } // getIndex方法通过遍历存放顶点的泛型数组找到顶点的索引值,顶点在泛型数组中的索引值即为它在邻接矩阵中的索引值 public int getIndex(T vertex) { for (int i = 0;i < numVertices;i++){ if (vertices[i] == vertex){ return i; } else{ return -1; } } return -1; }addVertex方法:此方法用于向图中添加新的顶点,添加过程中有两个步骤,一是在泛型数组中添加该顶点,二是在邻接矩阵中增加一行和一列,并把其中所有恰当的位置都设为false。
public void addVertex(T vertex) { //当邻接矩阵满了的时候,对其进行扩容 if ((numVertices + 1) == adjMatrix.length) { expandCapacity(); } //步骤一:在泛型数组中添加该顶点 vertices[numVertices] = vertex; //步骤二:把邻接矩阵中的适当位置改为false for (int i = 0; i < numVertices; i++) { adjMatrix[numVertices][i] = false; adjMatrix[i][numVertices] = false; } numVertices++; modCount++; }expandCapacity方法:用邻接矩阵实现无向图中的扩容与其他用数组实现的扩容方法不同,它不仅要复制数组,还要对邻接矩阵进行复制和扩容。
protected void expandCapacity() { // 创建新的泛型数组和邻接矩阵 T[] largerVertices = (T[])(new Object[vertices.length*2]); boolean[][] largerAdjMatrix = new boolean[vertices.length*2][vertices.length*2]; // 外层循环进行泛型数组的复制,同时协助内层循环进行邻接矩阵的复制 for (int i = 0; i < numVertices; i++) { // 内层循环进行邻接矩阵的复制 for (int j = 0; j < numVertices; j++) { largerAdjMatrix[i][j] = adjMatrix[i][j]; } largerVertices[i] = vertices[i]; } // 将扩容后的二者赋值给原来的泛型数组和邻接矩阵 vertices = largerVertices; adjMatrix = largerAdjMatrix; }
教材学习中的问题和解决过程
- 问题1:在看书上关于如何生成最小生成树的内容时,不能理解树是怎么找出来的
- 问题1解决方案:当时看的时候,关于“下一步我们往minheap中添加所有含该新顶点且另一顶点尚不在最小生成树中的边”,我一开始的理解是每次加入新顶点后,边只能从与该顶点连接的边中选择,这样的话就与任选一个起始顶点冲突了,因为只有在选择特定顶点时才能找出最小生成树,选择其他顶点时都会有多余的边。后来我与我的结对伙伴张昊然同学进行了讨论,他一语点醒梦中人,原来是我对另一顶点尚不在最小生成树中的边理解有误,它说的是所有在最小堆中的边而不需要必须是最小堆中与最新顶点相连的边,因为最小堆中的边都满足一边的顶点在最小生成树中,另一顶点不在最小生成树中这一条件。
- 【补充】这周五上完课之后发现之前的理解并不是对的,书上给的Prim法要求的就是每一次都要以上一会新加入的结点为一段来寻找另一端不在最小生成树中的权重最小的边,Prim方法的核心是每次加入一个顶点,而我上面说的每次从最小堆中取出最小边的方法应该算是Kruscal方法,核心是每次添加一条权重最小的边。
- 问题2:用邻接列表实现无向图的代码实现
- 问题2:解决方法:邻接列表实现无向图相比用邻接矩阵实现我觉得其实要简单许多,主要体现在添加/删除边上,因为用邻接列表实现不需要通过循环来找到连接边的两个顶点的位置。
- 构造函数:在设置构造函数之前,需要设置一个列表来作为顶点集存储所有的顶点,每个顶点又要作为一个链表的头,所以还需要一个结点类,这个结点类可以用之前的也可以自己重新写一个,在这里我重新写了一个VerticeNode类
private ArrayList<VerticeNode> vertices; // 用于存储顶点 private int numVertices; // 记录顶点的个数 private int modCount; public LinearGraph(){ numVertices = 0; modCount = 0; a = 0; vertices = new ArrayList<VerticeNode>(); }- 添加顶点:将顶点的元素实例化为VerticeNode类后加入队列即可
@Override public void addVertex(Object vertex) { VerticeNode node = new VerticeNode(vertex); vertices.add(node); modCount++; numVertices++; }- 删除顶点:删除顶点分为两步,第一步是直接将顶点从顶点列表里删除,第二步是将顶点列表中所删除顶点之后的顶点全部前移,保持列表的连贯性。
@Override public void removeVertex(Object vertex) { int i = 0; // 将目标顶点删除 while (vertices.get(i).getElement() != vertex){ i++; } vertices.remove(i); // 将顶点之后的列表里的元素前移 for (int j = 0;j < numVertices;j++){ VerticeNode temp = vertices.get(j); while (temp.getNext() != null){ if (temp.getNext().getElement() == vertex){ temp.setNext(temp.getNext().getNext()); } temp = temp.getNext(); } break; } modCount--; numVertices--; }- 添加边:添加边时首先要找到顶点所在的位置,在找到之后将另外一个顶点添加到该顶点的链表末尾,接着再对另一个顶点进行相同的操作。
@Override public void addEdge(Object vertex1, Object vertex2) { // 寻找顶点要被添加的位置 int i = 0; while (vertices.get(i).getElement() != vertex1){ i++; } // 在顶点一的链表末端添加顶点二,在两顶点之间建立边 VerticeNode temp = vertices.get(i); while (temp.getNext() != null){ temp = temp.getNext(); } temp.setNext(new VerticeNode(vertex2)); // 对顶点二的链表进行上述相同操作 int j = 0; while (vertices.get(j).getElement() != vertex2){ j++; } VerticeNode temp1 = vertices.get(j); while (temp1.getNext() != null){ temp1 = temp1.getNext(); } temp1.setNext(new VerticeNode(vertex1)); }- 删除边:在删除边时,首先要找到所删除的边的两端顶点的位置,在进行删除时分为两种情况,一是所删除的结点位于链表末端,二是所删除的结点位于链表中间。
@Override public void removeEdge(Object vertex1, Object vertex2) { // 找到所要删除的顶点的位置 int i = 0; while (vertices.get(i).getElement() != vertex1){ i++; } // 在顶点一的链表中找到顶点二的前驱结点 VerticeNode temp = vertices.get(i); while (temp.getNext().getElement() != vertex2){ temp = temp.getNext(); } // 如果顶点二位于末端,直接将temp的next设为空即可 if (temp.getNext().getNext() == null){ temp.setNext(null); } // 如果顶点二位于中间,将temp的next设置为顶点二的next即可 else { temp.getNext().setNext(temp.getNext().getNext()); } }
## 代码调试中的问题和解决过程
- 问题一:在测试PP15.1时,输出的全为null
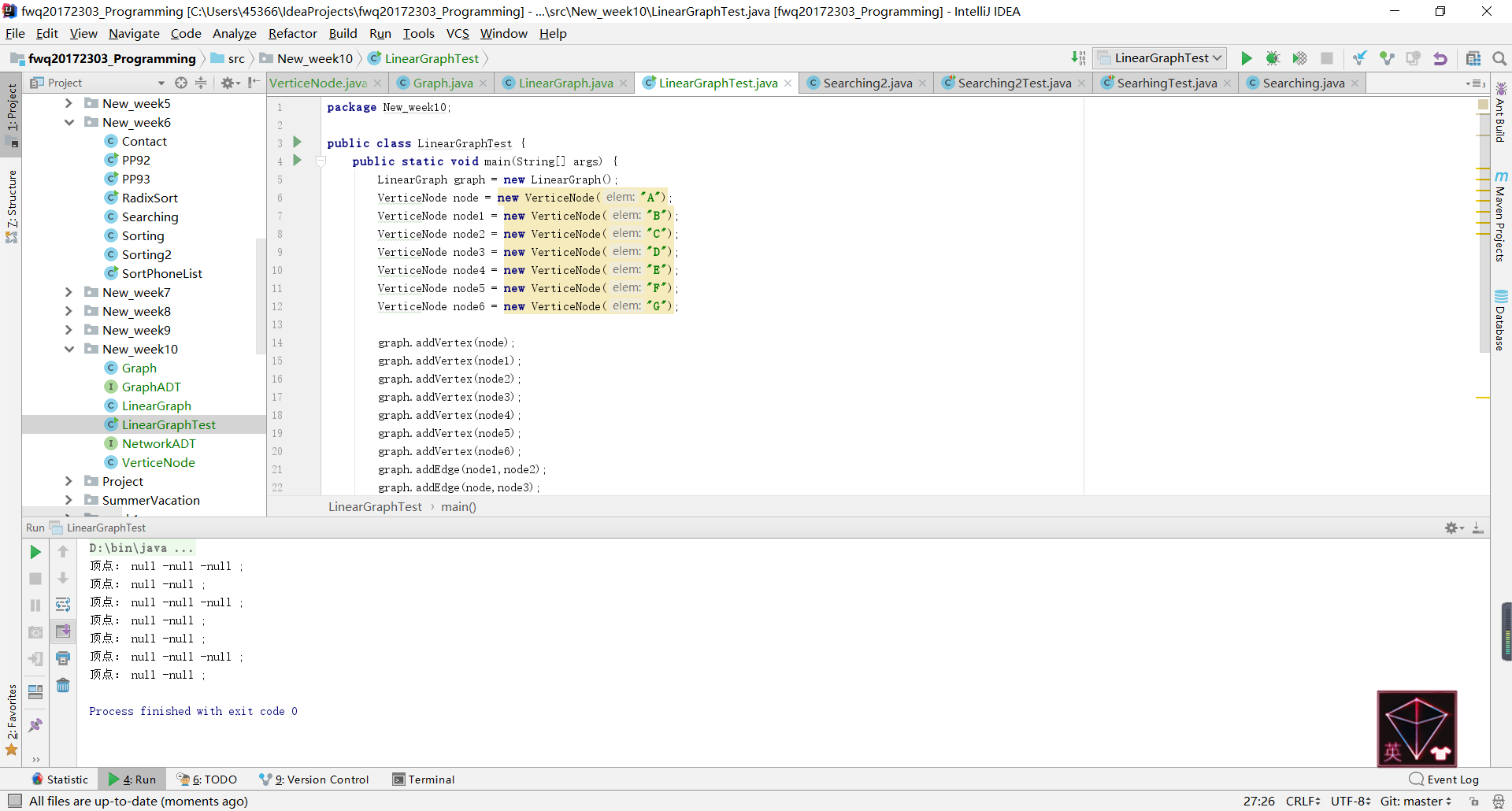
- 问题一解决方法:我通过Debug发现赋值是赋值好了的,但是每一个node结点虽然有值,但是仍然显示为空。

- 后来询问了结对伙伴之后他说不要把顶点设置成``VerticeNode``类,直接进行添加就可以了。

## [代码托管](https://gitee.com/CS-IMIS-23/fwq20172303_Programming.git)
- 上周代码量:18061

## 上周考试错题总结(正确为绿色,错误为红色)
上周没有测试。
## 结对及互评
### 点评模板:
- 博客中值得学习的或问题:
- 我的结对伙伴现在在教材内容总结方面一直保持着很认真的态度,但是希望今后的教材总结可以在内容丰富的基础上更加条理一点~除此之外他的问题总结方面还是一如既往地保持了坦诚直接的风格,有问题就是有问题,没问题就是没问题,继续加油吧~
### 点评过的同学博客和代码
- 本周结对学习情况
- [20172322](https://www.cnblogs.com/zhangyeye233/p/9979791.html)
- 结对学习内容
- 教会了我博客园修改字体样式的方法。
- 交流了课本内容。
## 其他(感悟、思考等,可选)
- 感觉自己最近对java的学习有点不像以前那么上心了,而且很爱拖沓,接下来要努力把剩下的课程坚持下来。
## 学习进度条
| | 代码行数(新增/累积)| 博客量(新增/累积)|学习时间(新增/累积)|重要成长|
| -------- | :----------------:|:----------------:|:---------------: |:-----:|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 10/10 | 1/1 | 10/10 |
| 第二周 | 246/366 | 2/3 | 20/30 |
| 第三周 | 567/903 | 1/4 | 10/40 |
| 第四周 | 2346/3294 | 2/6 | 20/60 |
| 第五周 | 2346/3294 | 2/8 | 30/90 |
| 第六周 | 1343/4637 | 2/8 |20/110 |
| 第七周 | 654/5291 | 1/9 | 25/135 |
| 第八周 | 2967/8258 | 1/10 | 15/150 |
| 第九周 | 2871/11129 | 2/12 | 20/170 |
- 计划学习时间:20小时
- 实际学习时间:20小时
- 改进情况:因为经历了树之后其实我对学习图还是挺害怕的,幸运的是它没有我想的那么难,太好了。
## 参考资料
- [拓扑排序](https://baike.baidu.com/item/%E6%8B%93%E6%89%91%E6%8E%92%E5%BA%8F/5223807?fr=aladdin)
- [图的java实现](https://blog.csdn.net/xu__cg/article/details/51912098)
- [java图的邻接表实现两种方式及实例应用分析](https://blog.csdn.net/feilong_csdn/article/details/69321375)