20172303 2018-2019-1《程序设计与数据结构》第7周学习总结
教材学习内容总结
本周在上周学习了二叉树的基础上,学习了一种二叉树的特殊形式——二叉查找树,又叫有序二叉树、排序二叉树。本章学习了两种二叉查找树的实现方法,以及两种二叉查找树的应用。
一、概述
1.二叉查找树
- 概念:树中的所有结点,其左孩子都小于父结点,父结点小于或等于其右孩子。
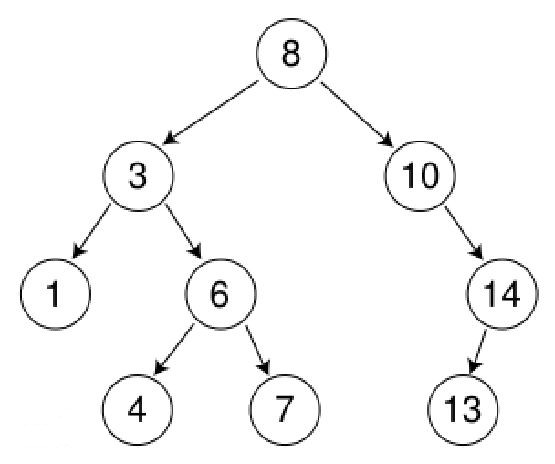
- 性质:
- 任意结点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 任意结点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 任意结点的左、右子树也分别为二叉查找树;
- 没有元素相等的结点。
2.二叉查找树ADT
- 二叉查找树的ADT是上一章中讨论的二叉树的扩展,其中的操作是二叉树中已定义的那些操作的补充。
- 二叉查找树中的操作:
addElement:向树中添加一个元素removeElement:从树中删除一个元素removeAllOccurrences:从树中删除所指定元素的任何存在removeMin:删除树中的最小元素removeMax:删除树中的最大元素findMin:返回树中的最小元素的引用findMax:返回树中的最大元素引用
二、二叉查找树的实现
1.查找
- 二叉查找树的查找方法与二分查找类似,将所要查找的元素与根结点的元素进行比较,如果小于根结点则继续与左孩子对比,大于根结点则继续与右孩子对比,如果相等则返回元素。实现方法有迭代和递归两种。
- 迭代实现
public void find(T element)
{
T result = null;
BinaryTreeNode node = root;
while (node != null)
{
if (element.CompareTo(node.getElement) > 0)
{
node = node.right;
}
else if (element.CompareTo(node.getElement) < 0)
{
node = node.left;
}
else
{
result = node.getElement;
break;
}
}
return result;
}
- 递归实现
public void find(T element)
{
return find(root, element);
}
private void find(BinaryTreeNode root, T element)
{
if (root == null) {
return element;
}
int comparable = element.CompareTo(root.getElement);
if (comparable > 0){
find(root.right,element);
}
else if (comparable < 0){
find(root.left,element);
}
else {
return root.getElement;
}
}
2.插入
- 进行插入的操作有三种情况:
- 若当前的二叉查找树为空,加入的元素会成为根结点。
- 若所插入结点的元素小于根结点的元素:
- 若根的左孩子为
null,插入结点将会成为新的左孩子。 - 若根的左孩子不为
null,则会继续对左子树进行遍历,遍历的同时进行比较操作。
- 若根的左孩子为
- 若所插入结点的元素大于或等于根结点的元素
- 若根的右孩子为
null,插入结点将会成为新的右孩子。 - 若根的右孩子不为
null,则会继续对右子树进行遍历,遍历的同时进行比较操作。
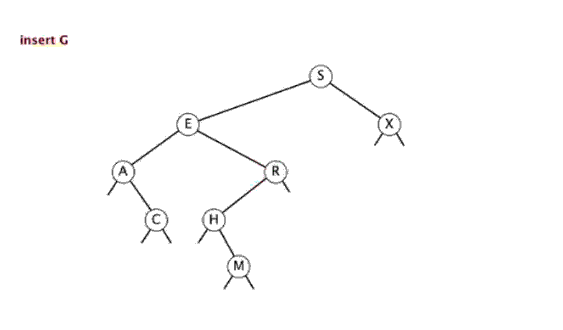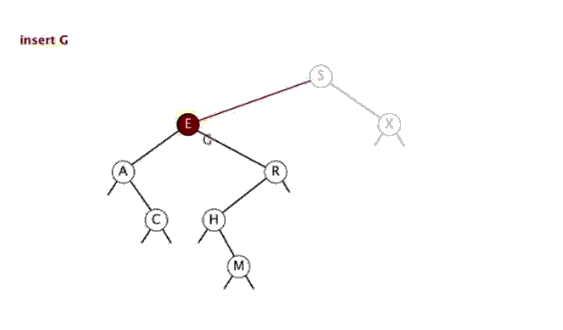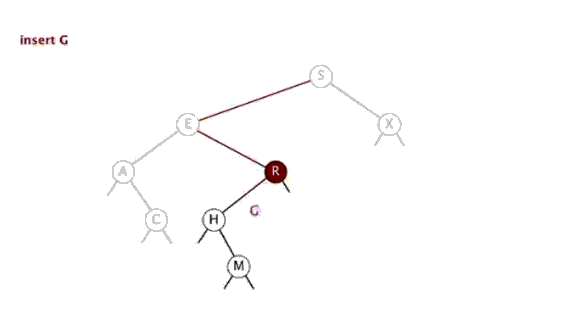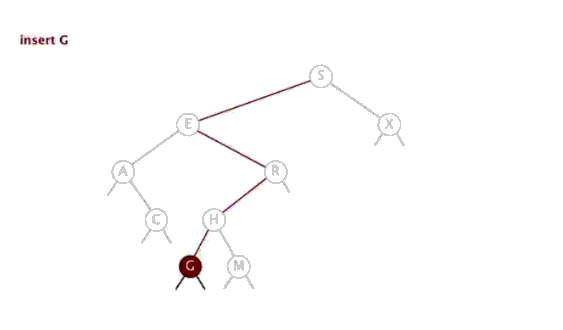
- 若根的右孩子为
3.删除
- 二叉查找树的删除操作是所有操作中最为复杂的,我们先来考虑一种特殊情况:所删除的元素是树中的最大值或最小值。
(1)特殊情况:所删除元素为树中的最大值或最小值
- 由于二叉查找树的特殊形式,其最小值一般位于树的左子树,最大值位于树的右子树。两者的删除方法是类似的,唯一不同的地方就是“左”和“右”,下面我们以删除最大值为例来说明,删除最小值的情况只要把例子中的“左”和“右”交换一下即可。
- 删除最大值有三种情况:
- 若根结点没有右孩子,那么根结点的元素就为最大元素,原树根的左孩子则会变成新的根结点。
- 若最大值的结点是一个叶子结点,那么直接将其父结点的右孩子的引用设置为
null即可。 - 若最大值的结点是一个中间结点,则需要设置其父结点的右孩子的引用为该结点的左孩子。
(2)正常情况
- 正常情况下删除元素也有三种情况,但这三种情况就不是那么简单了。
- 情况一:所删除的为叶子结点
- 这种情况下可以直接删除该结点。不论该结点是根结点还是普通的有父类的叶子结点,都直接将
root或父结点与之连接的指针设置为空即可。

- 这种情况下可以直接删除该结点。不论该结点是根结点还是普通的有父类的叶子结点,都直接将
- 情况二:所删除的单支结点(即只有左子树或右子树)
- 当删除的结点是根结点时,将
root指针指向被删除结点的单支(左子树或右子树) - 当删除的结点只有左子树时,将所删除结点的父结点的指针指向所删除结点的左孩子。当删除的结点只有右子树时,将所删除结点的父结点的指针指向所删除结点的右孩子。

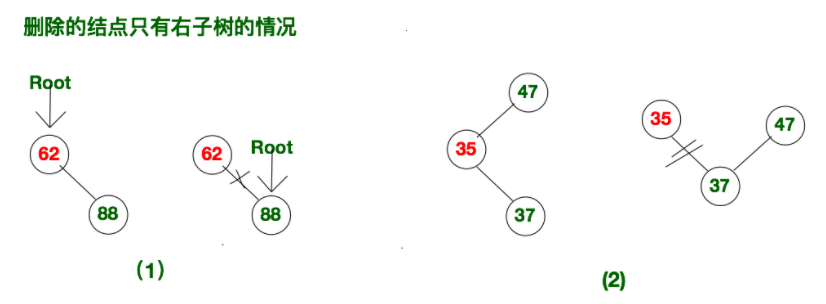
- 当删除的结点是根结点时,将
- 情况三:所删除的结点既有左子树又有右子树
- 这里需要了解两个概念——前驱结点和后继结点。分别是树中小于它的最大值和大于它的最小值,如果把树结构中的所有节点按顺序排好的话,它的前驱和后继两个结点刚好在它的左右。当一个节点被删除时,为了保证二叉树的结构不被破坏,要让它的前驱结点或者后继结点来代替它的位置,然后将它的前驱结点或者后继结点做同样的删除操作。

- 将当前结点与左子树中最大的元素交换,然后删除当前结点。左子树最大的元素一定是叶子结点,交换后,当前结点即为叶子结点,其删除方式即可参考情况一。还可以将当前结点与右子树中最小的元素交换,然后删除当前结点。
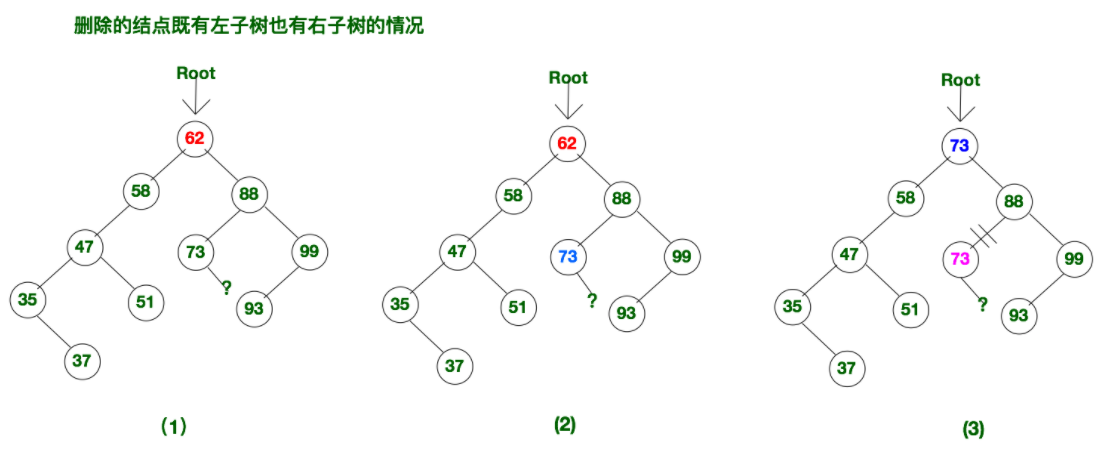
- 这里需要了解两个概念——前驱结点和后继结点。分别是树中小于它的最大值和大于它的最小值,如果把树结构中的所有节点按顺序排好的话,它的前驱和后继两个结点刚好在它的左右。当一个节点被删除时,为了保证二叉树的结构不被破坏,要让它的前驱结点或者后继结点来代替它的位置,然后将它的前驱结点或者后继结点做同样的删除操作。
三、应用——平衡二叉查找树
1.使二叉查找树平衡的方法
- 会有两种方式使二叉查找树变得不平衡:插入元素或删除元素。如果二叉查找树不平衡,其效率可能比线性结构还要低。我们的目标是保持树的最大路径长度接近log2n。为了使树达到平衡,我们有四种方法:右旋、左旋、右左旋和左右旋。
- 左旋和右旋
- 左旋和右旋是针对不平衡因素是叶子结点的情况,在这种情况下,将根结点的左孩子/右孩子(与不平衡的子树相反的一方)成为新的根结点,然后使原树根的左孩子的右孩子(右孩子的左孩子)成为原树根的新的右孩子(左孩子)

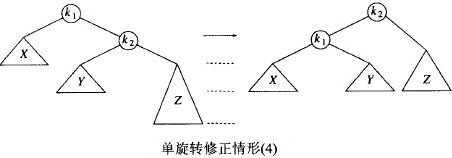
- 左旋和右旋是针对不平衡因素是叶子结点的情况,在这种情况下,将根结点的左孩子/右孩子(与不平衡的子树相反的一方)成为新的根结点,然后使原树根的左孩子的右孩子(右孩子的左孩子)成为原树根的新的右孩子(左孩子)
- 右左旋和左右旋
- 右左旋和左右旋是针对不平衡因素是内部结点的情况,在这种情况下,要先针对不平衡因素所在的子树进行一次左旋/右旋(与不平衡的子树相同的一方),然后再针对新得到的树根进行与之前相反的一次操作。
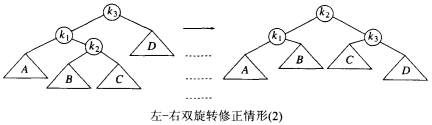
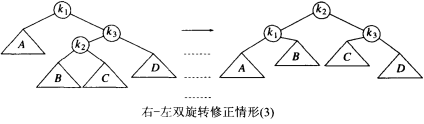
- 右左旋和左右旋是针对不平衡因素是内部结点的情况,在这种情况下,要先针对不平衡因素所在的子树进行一次左旋/右旋(与不平衡的子树相同的一方),然后再针对新得到的树根进行与之前相反的一次操作。
2.AVL树
- AVL树是一种带有平衡条件的二叉查找树。这个平衡条件必须容易保持,而且它保证树的深度必须是O(logn)。在一颗AVL树中,其每个结点的左子树和右子树的高度最多相差|1|(空树的高度定义为-1)。即平衡因子(右子树高度-左子树高度)最多为|1|。
- 对AVL树进行插入操作可能会使其失去平衡的条件,但这可以通过对树进行简单的修正来保持其平衡的属性,这种操作就是我们刚刚在上面所讲的四种方法。
- 结点的平衡因子大于等于+2,其左孩子的平衡因子为-1——左旋
- 结点的平衡因子小于等于-2,其右孩子的平衡因子为+1——右旋
- 结点的平衡因子为+2,其右孩子的平衡因子为-1——右左旋
- 结点的平衡因子为-2,其左孩子的平衡因子为+1——左右旋
3.红黑树
- 概念:红黑树是平衡二叉树的另一种实现,它的每个结点都存储一种颜色——红色或者黑色。控制结点颜色的规则为:
- 根结点和叶子节点为黑色。
- 红色结点的孩子都为黑色。
- 从树根到叶子的每条路径都包含相同数目的黑色结点。

红黑树的插入
- 情况一:当前结点的父结点是红色,祖父结点的另一个子结点(叔叔结点)是红色。
- 对策:将当前结点的父结点和叔叔结点变为黑色,祖父结点变为红色,再把当前结点指向祖父结点,从新的当前结点重新开始算法。
- 情况二:当前结点的父结点是红色,叔叔结点是黑色,当前结点是其父结点的右子树
- 对策:当前结点的结点做为新的当前结点,针对新的当前结点进行一次左旋。
- 情况三:当前结点的父结点是红色,叔叔结点是黑色,当前结点是其父结点的左子树
- 对策:将父结点变为黑色,祖父结点变为红色,针对祖父结点进行一次右旋。
红黑树的删除
- 红黑树的操作较为复杂,但是这篇博客中的介绍比较详细具体,它把删除红黑树的操作分成了三类,第一类是删除的结点为叶子结点,第二类是删除的结点有一个子树(这里博客中分成了有左子树和右子树两种情况)第三类是删除的结点既有左子树又有右子树。但其实红黑树的删除操作不是难点,难点在于删除之后的平衡处理,在这篇博客中讲的非常详细,我就不再赘述了。
教材学习中的问题和解决过程
- 问题1:递归和迭代的区别在哪里?
- 问题1解决方案:
- 概念不同:程序调用自身的编程技巧称为递归,其实就是函数自己调用自己。迭代是指利用变量的原值推算出变量的一个新值,如果递归是自己调用自己的话,迭代就是A不停的调用B。
- 使用的方法不同:迭代使用的是循环(for,while,do-while)或者迭代器,当循环条件不满足时退出。而递归一般是函数递归,可以是自身调用自身,也可以是非直接调用,即方法A调用方法B,而方法B反过来调用方法A,递归退出的条件为if-else语句,当条件符合基的时候退出。
- 对比:递归的代码比较简单易懂,实现一个计算逻辑往往只需要很短的代码就能解决。但是由于它要不停地调用函数,就可能浪费大量的空间。递归中函数调用的局部状态是用栈来记录的,所以如果递归太深的话还有可能导致堆栈溢出。而对于迭代而言,能使用递归实现的都可以使用迭代来实现,并且效率会很高,在空间消耗上也很小,唯一的缺点就是代码比较难懂。
- 总结:递归中一定有迭代,但是迭代中不一定有递归,大部分可以相互转换。能用迭代的不要用递归,递归调用函数不仅浪费空间,如果递归太深的话还容易造成堆栈的溢出。
- 问题2:在讨论AVL树的平衡化过程中,为什么孩子结点的平衡因子不会为+2或-2?
- 问题2解决方法:平衡化操作在删除或插入结点之后进行,在这一过程中,平衡化从因为删除或插入操作而改变的结点处开始,之后沿着路径一直上溯到根结点为止。在这一过程中,会根据情况进行旋转,因此我们永远不会遇到父结点和孩子结点的平衡因子都为|2|的情况,因为在抵达父结点前孩子结点的平衡因子已经被修正过了。
- 问题3:红黑树最长路径遍历的时间复杂度为多少?
- 问题3解决方法:因为红黑树“红色结点的孩子必须都为黑色”的性质,所以一颗红黑树中的任意一条路径中,至多有一半的结点是红色结点,至少有一半的结点是黑色结点,所以红黑树的最大深度为2logn,因此红黑树最长路径遍历的时间复杂度为O(logn)。
代码调试中的问题和解决过程
- 问题1:在实现PP11.3时,虽然删除/查找最大值和最小值都能实现,但是无法把树输出
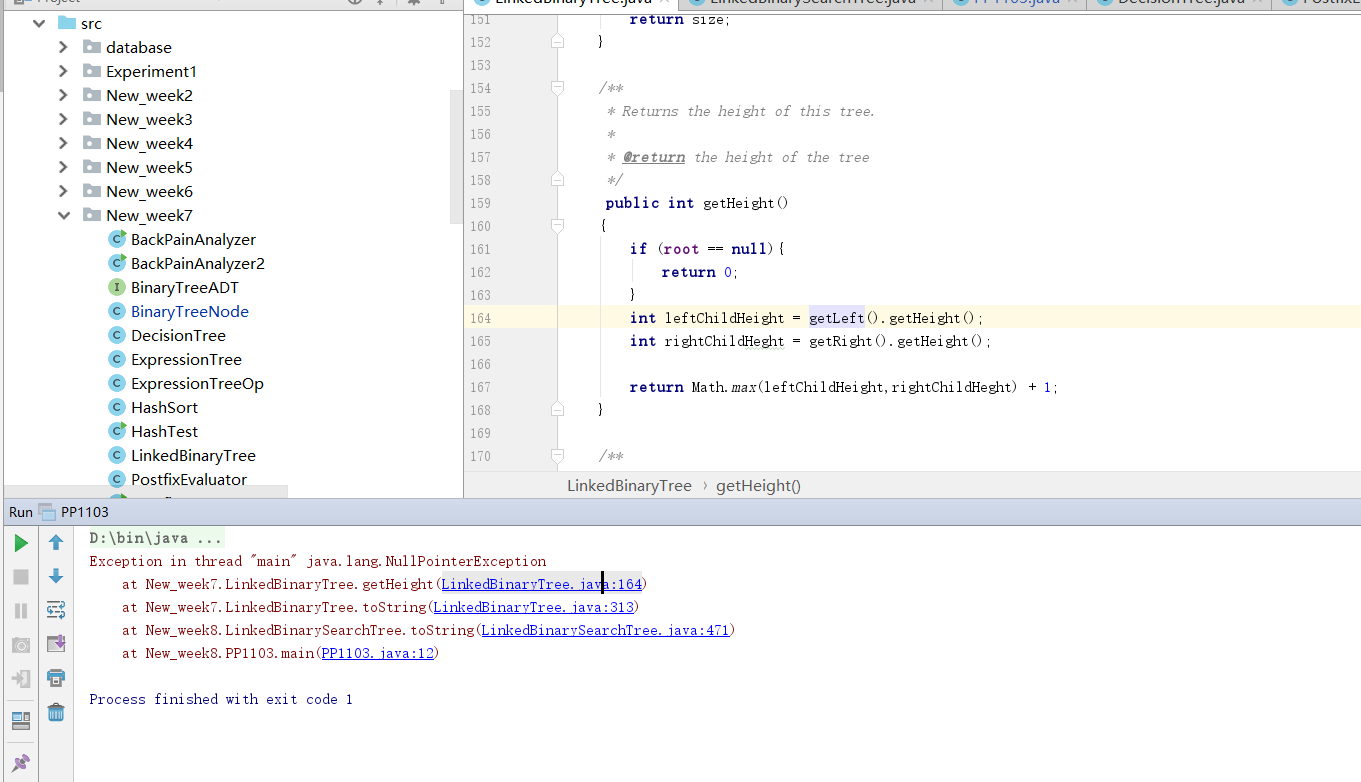
- 问题1解决方法:抛出错误的提示说问题是出在
LinkedBinaryTree里面的getHeight方法中,但是我非常不理解为什么抛出的会是NullPointerException。于是去查了一下会抛出NullPointerException异常的原因有哪些,一般有三种:字符串变量未初始化;接口类型的对象没有用具体的类初始化;当一个对象的值为空时,没有判断为空。 - 但是我又觉得这个异常的抛出好像都不是这三种,应该是因为所要输出的树不是满树的原因,因为当时做课堂测试计算背部疼痛诊断器的高度时修改过
getHeight的代码,但背部疼痛诊断器是一颗满树,如果当我建立的树不是一颗满树时,在gerHeight调用getLeft或者getRight的时候,一定会出现指针为空的情况,然后就会抛出异常,所以我就将gerHeight的方法改回来了。
public int getHeight()
{
// if (root == null){
// return 0;
// }
// int leftChildHeight = getLeft().getHeight();
// int rightChildHeght = getRight().getHeight();
//
// return Math.max(leftChildHeight,rightChildHeght) + 1;
int result = height(root);
return result;
}
- 但是在修改之后再次测试时又出现了新的错误。
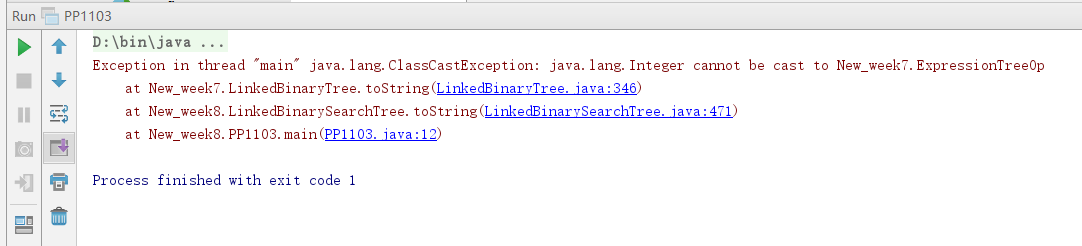
- 不过这个错误就很好解决了,因为当初发现
ExpreesionTree中的PrintTree方法可以直接用作LinkedBinaryTree中的toString方法我就直接复制粘贴过来了,但是没有改变相应的类型,在把所有的ExpreesionTreeOp类型改成Integer类型后,程序就能完美地输出树了。

代码托管
- 上周代码量:14440

上周考试错题总结(正确为绿色,错误为红色)
上周考试无错题。
结对及互评
点评模板:
- 博客中值得学习的或问题:
- 可以明显地感觉出来我的结对伙伴对于课本内容的自己的理解部分越来越多了,虽然他对自己第五周的评分有些失落,但是我相信努力是一定会有收获的!除此之外博客里的每一个“红黑树”真的都好俏皮啊哈哈哈哈,不过图片的排版似乎有问题?
- 代码中值得学习的或问题:
- 代码中的备注变多了,值得夸奖。
点评过的同学博客和代码
- 本周结对学习情况
- 20172322
- 结对学习内容
- 讨论了AVL树的代码实现。
- 讨论了书上P242图11.16的错误。
其他(感悟、思考等,可选)
- 其实上周刚开始学树的时候感觉自己都是稀里糊涂的,代码也不是很懂会有很多错误,但是当时因为时间比较紧张所以都是囫囵吞枣做完的,但是这周在学习新的东西的时候发现有些上一章我糊弄过去的东西如果不搞懂搞明白的话是做不出来的,所以又去返工把之前的东西搞明白搞好,所以说学习还是要踏实啊,真的一点都不能轻易放松。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 10/10 | 1/1 | 10/10 | |
| 第二周 | 246/366 | 2/3 | 20/30 | |
| 第三周 | 567/903 | 1/4 | 10/40 | |
| 第四周 | 2346/3294 | 2/6 | 20/60 | |
| 第五周 | 1343/4637 | 2/8 | 30/90 | |
| 第六周 | 1343/4637 | 2/8 | 20/110 | |
| 第七周 | 654/5291 | 1/9 | 25/135 |
- 计划学习时间:20小时
- 实际学习时间:25小时
- 改进情况:上个星期学习的时候偶然查到了红黑树,当时没仔细看还觉得挺好玩的,真正这个学期学起来才发现它有多恐怖...