【二分答案】Expanding Rods POJ 1905

题目链接：http://poj.org/problem?id=1905

题目大意：原长度为L的线段因受热膨胀为一段弧，线段L、弧长L‘、温度n、膨胀率c满足L' =(1+n/c)*L;求线段的中点移动的最小距离。

’？‘代表的线段就是要求的距离。

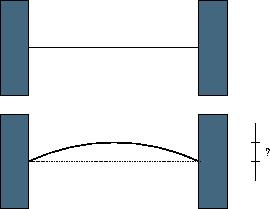
怎么办呢？用分治，二分答案，验证弧长是否为目标弧长再进行调整。

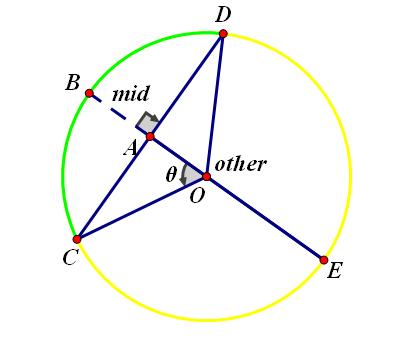
首先利用相交弦定理[BA×EA=CA×DA]算出other(AE)

然后用(mid+other)/2得到r(CO)

再用r-mid(AO)除以r(CO)算出cos(θ)

再用acos算出θ,然后算出弧长

贴代码:

#include<cstdio>  
#include<cmath>
using namespace std;
double L,n,c,_L;
int main()
{
	while(scanf("%lf%lf%lf",&L,&n,&c),L>=0)
	{   _L=(1+n*c)*L;
		if(L==0||n==0||c==0){puts("0.000");continue;}//特判,不然后面会除以0
		double l=0,r=L/2;
		while(l<r-(1e-6))//注意精度,太大会WA,太小会TLE
		{
			double mid=(l+r)/2,other=L*L/(mid*4);
			double R=(mid+other)/2,cos_sita,sita;
			cos_sita=(R-mid)/R;sita=acos(cos_sita);
			double hc=R*sita*2;
			if(hc>_L) r=mid;
			else l=mid;
		}
		printf("%.3lf
",l);
	}
}