初学 Size Balanced Tree（bzoj3224 tyvj1728 普通平衡树）

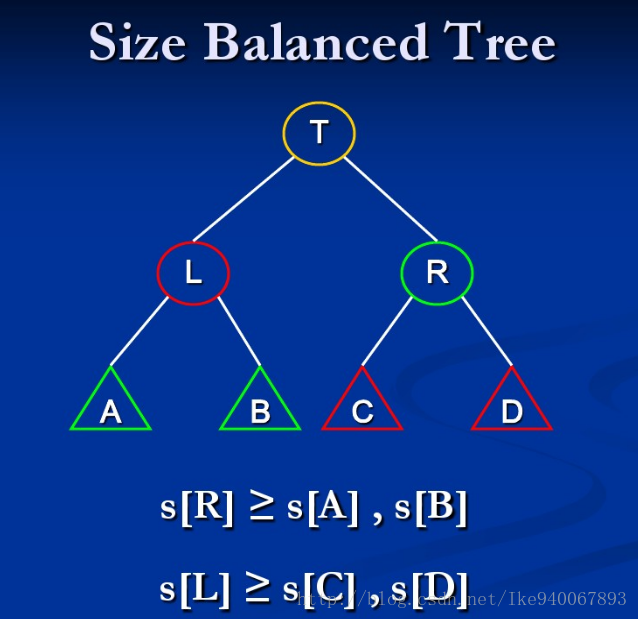
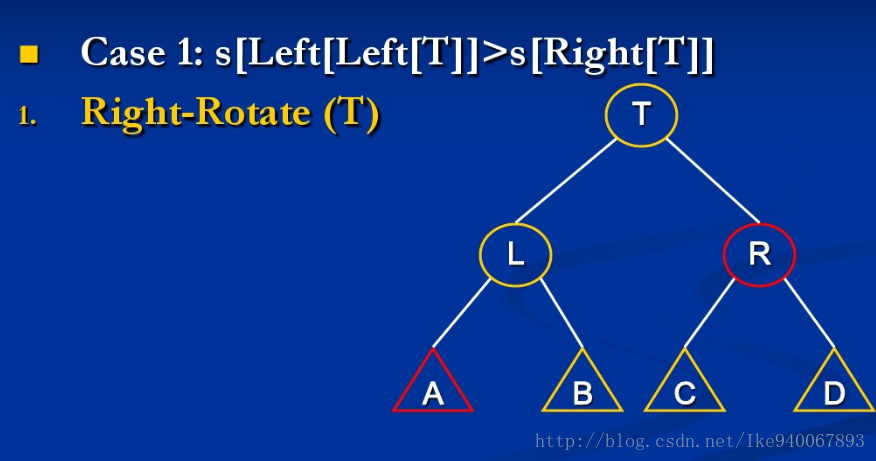
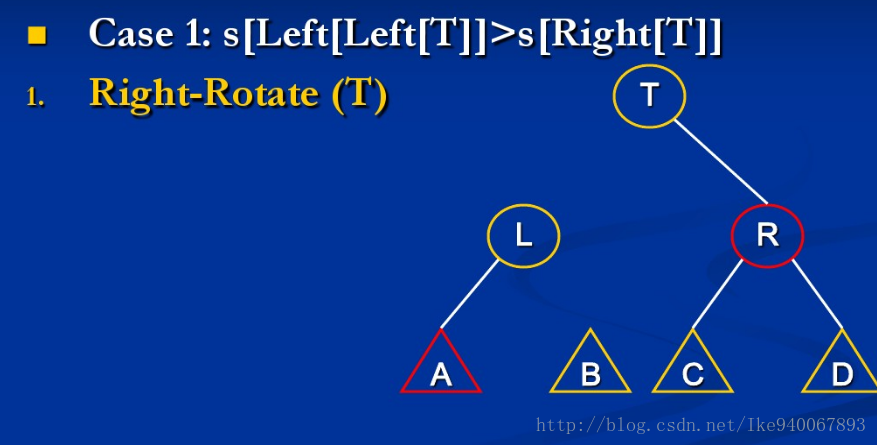
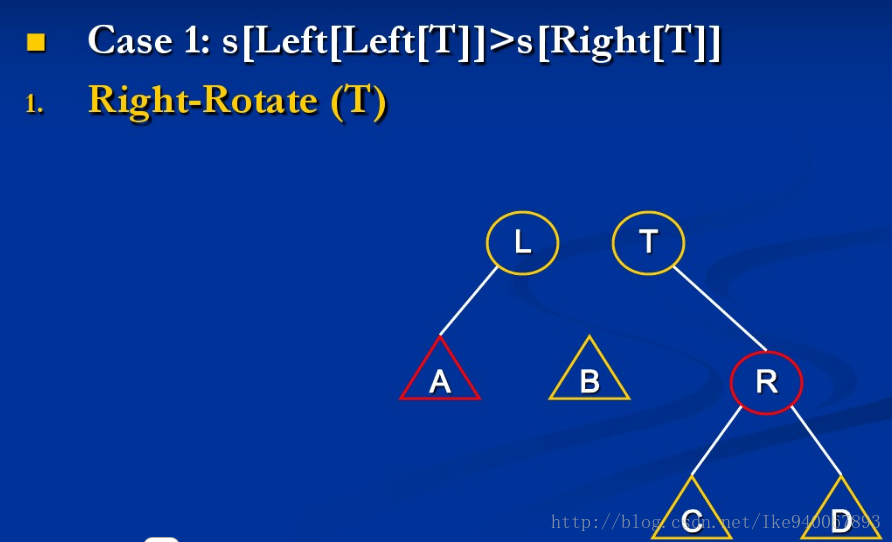
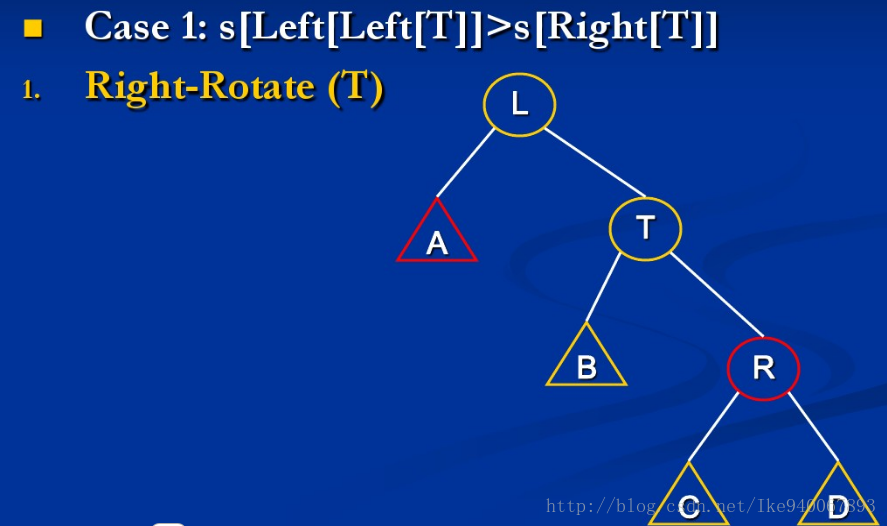
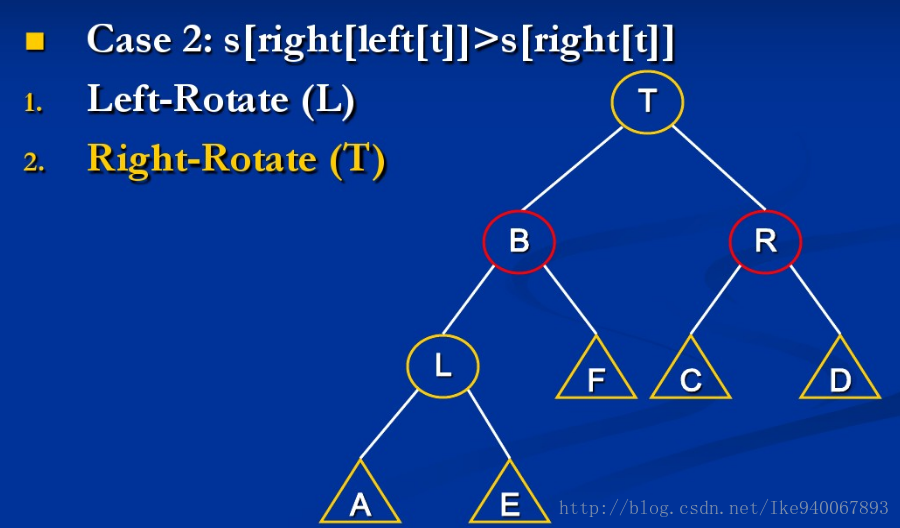
SBT（Size Balance Tree）， 即一种通过子树大小（size）保持平衡的BST

SBT的基本性质是：每个节点的size大小必须大于等于其兄弟的儿子的size大小：

当我们插入或者删除一个节点之后，SBT的性质会有所改变，此时需要函数maintain(mt)来维持平衡

mt(T)用于修复以T为根的子树的SBT 调用mt(T)的前提是T的子树都已经是SBT了

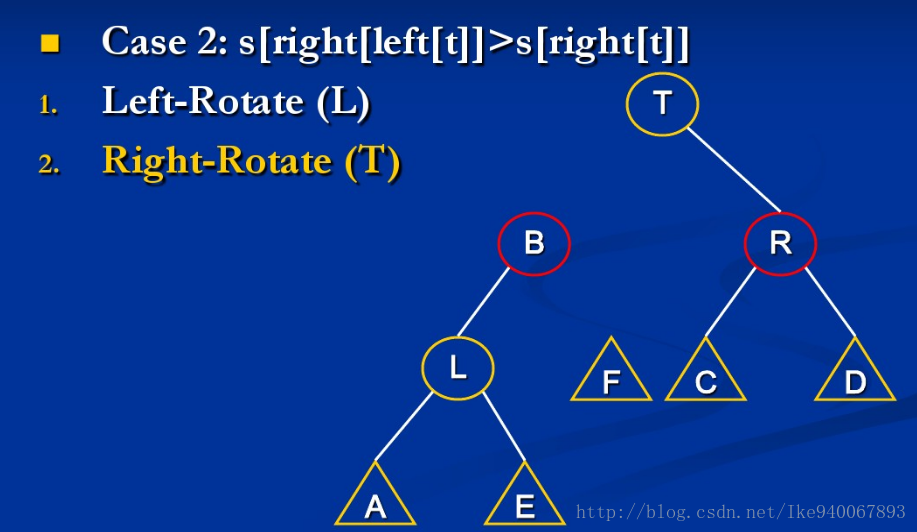
{由于左右对称，这里只讨论关于上图第一个不等式不成立的例子}

情形1：size[A] > size[R]

此时只需继续mt(A)与mt(L)就行

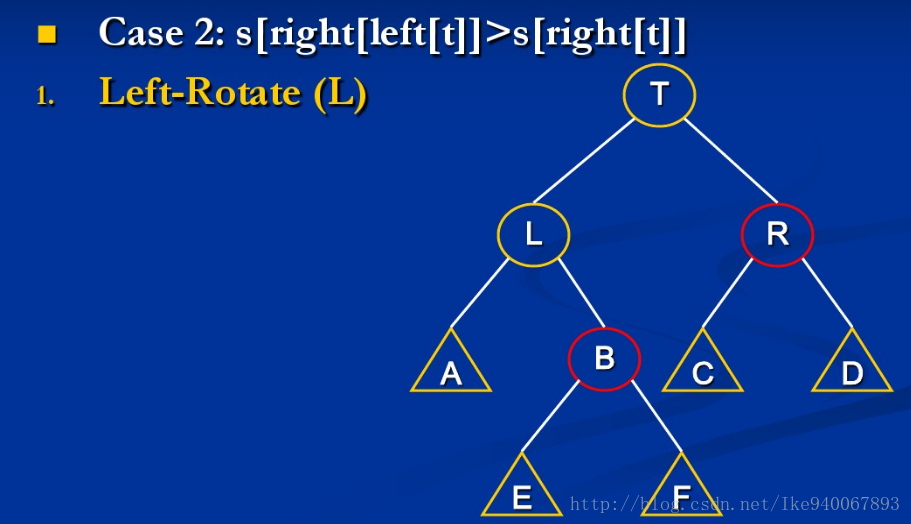
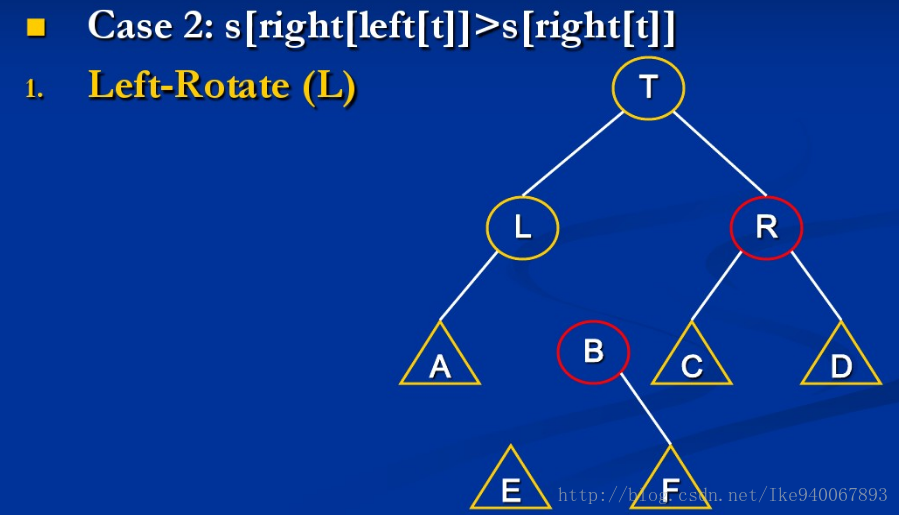
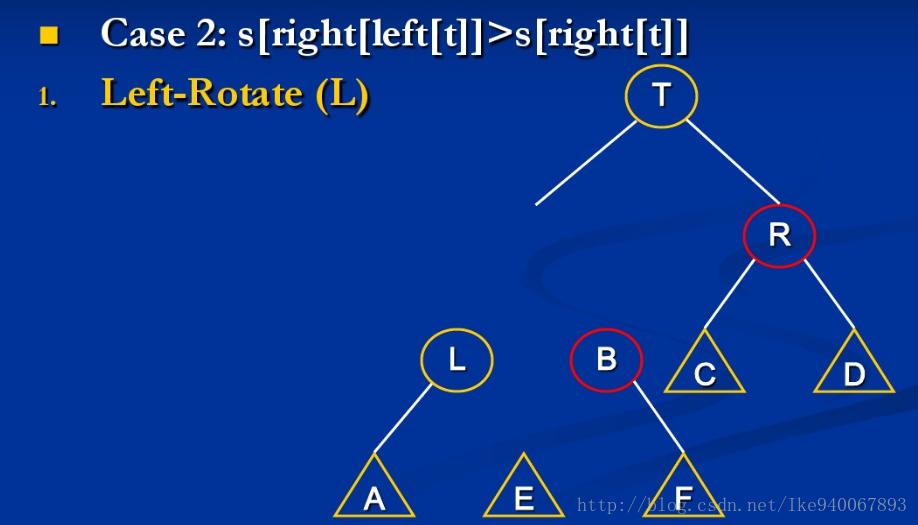
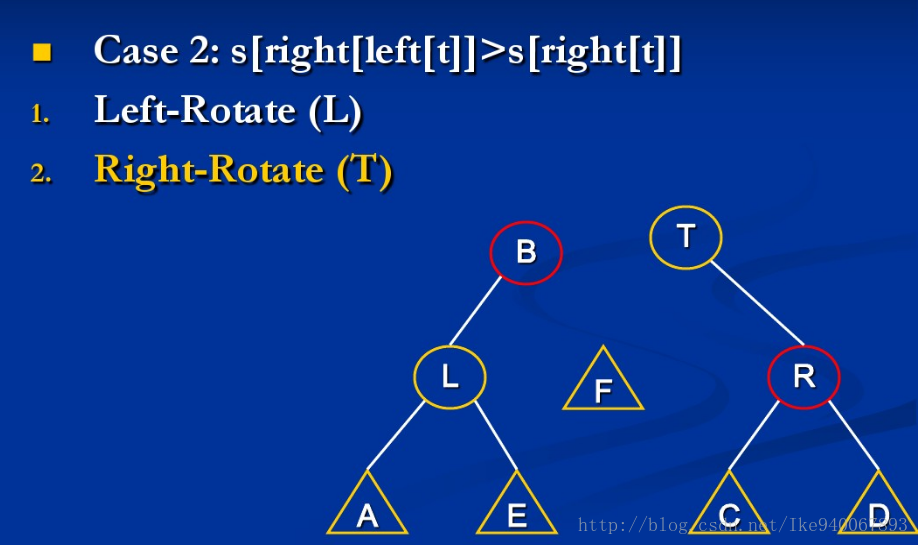
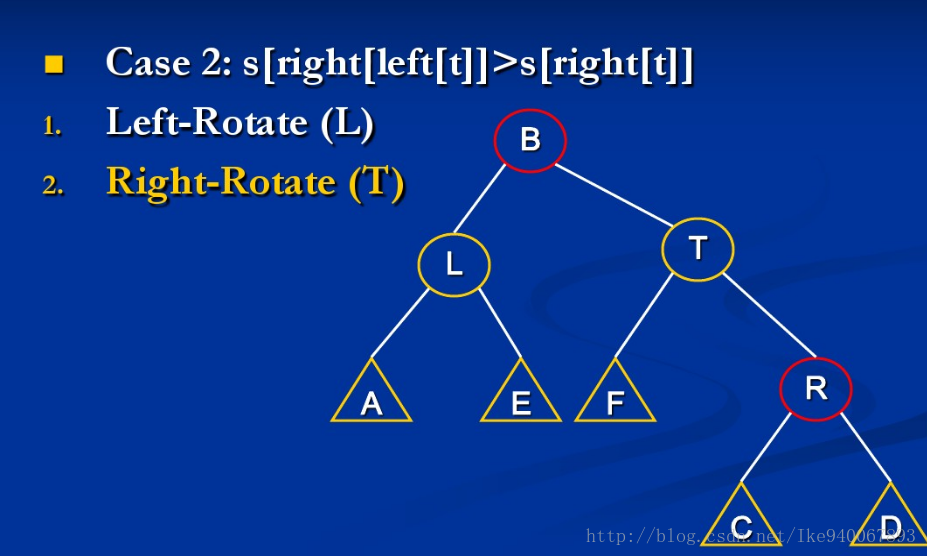
情形2：size[B] > size[R]

此时继续mt(L)与mt(B)

综上，Maintain代码如下：

inline void update(node* r) { r->sz = r->lc->sz + r->rc->sz + 1; }

void rotate(node* &r, bool f) {
    node *t = r->ch[f];
    r->ch[f] = t->ch[!f];
    t->ch[!f] = r;
    t->sz = r->sz;
    update(r);
    r = t;
}

void mt(node* &r, bool f) { //利用左右对称带上参数f同时减去不必要的检查
    if(r == NILL) return; //NILL 为空指针
    if(r->ch[f]->ch[f]->sz > r->ch[!f]->sz)
        rotate(r, f);
    else if(r->ch[f]->ch[!f]->sz > r->ch[!f]->sz)
        rotate(r->ch[f], !f), rotate(r, f);
    else return;
    mt(r->ch[f], f);
    mt(r, f);
}

Analysis of Height

F[H]:高度为H最大结点个数，有定理：

F[H] = Fibonacci[H+2]-1

∴N个结点的SBT的最坏深度最大满足（F[H]<=N）的H，因此：

根据各种分析之后可得：Maintain的单次操作为O(1) SBT的其他操作时间复杂度都为为log(n)

所以SBT被称为目前最快的二叉平衡树！贴上模板题的代码（普通平衡树）：

#include <cstdio>
#include <algorithm>
using namespace std;
#define lc ch[0]
#define rc ch[1]

const int MAXN = 500000;
const int INF = 0x3f3f3f3f;

struct node {
    node* ch[2];
    int sz, v;
    node(){}
}SBT[MAXN+10], *NILL=new node, *root=NILL, *tot=SBT;

int getint() {
    int ret = 0; bool f = 0; char ch;
    while((ch=getchar()) < '0' || ch > '9')if(ch == '-') f = !f;
    while(ch >= '0' && ch <= '9') ret = ret * 10 + ch - '0', ch = getchar();
    return f ? -ret : ret;
}

void init() {
    NILL->lc = NILL;
    NILL->rc = NILL;
    NILL->sz = 0;
}
inline void update(node* r) { r->sz = r->lc->sz + r->rc->sz + 1; }
node* newnode() {
    tot->lc = tot->rc = NILL;
    tot->sz = 1;
    return tot++;
}

void rotate(node* &r, bool f) {
    node *t = r->ch[f];
    r->ch[f] = t->ch[!f];
    t->ch[!f] = r;
    t->sz = r->sz;
    update(r);
    r = t;
}

void mt(node* &r, bool f) {
    if(r == NILL) return;
    if(r->ch[f]->ch[f]->sz > r->ch[!f]->sz)
        rotate(r, f);
    else if(r->ch[f]->ch[!f]->sz > r->ch[!f]->sz)
        rotate(r->ch[f], !f), rotate(r, f);
    else return;
    mt(r->ch[f], f);
    mt(r, f);
}

void insert(node* &r, int v) {
    if(r == NILL) {
        r = newnode();
        r->v = v;
        return;
    }
    r->sz++;
    bool k = v > r->v;
    insert(r->ch[k], v);
    mt(r, k);
}

int del(node* &r, int x) {
    int ret;
    r->sz--;
    if(r->v == x || (r->lc == NILL && x < r->v) || (r->rc == NILL && x > r->v)) {
        ret = r->v;
        if(r->lc == NILL || r->rc == NILL)
            r = r->lc==NILL ? r->rc : r->lc;
        else r->v = del(r->lc, x);
    }
    else ret = del(r->ch[x>=r->v], x);
    return ret;
}

int sel(int val) {
    int ret = 1;
    node* p = root;
    while(p != NILL) {
        if(val <= p->v)
            p = p->lc;
        else {
            ret += p->lc->sz + 1;
            p = p-> rc;
        }
    }
    return ret;
}

int rk(int x)
{
    node* p = root;
    while(p != NILL){
        if(x == p->lc->sz + 1)
            return p->v;
        if(x <= p->lc->sz)
            p = p->lc;
        else {
            x -= p->lc->sz + 1;
            p = p->rc;
        }
    }
    return INF;
}

int query(int v, bool f)
{
    node* p = root;
    int ret = f ? INF : -INF;
    while(p != NILL) {
        if(p->v != v && (f == (p->v > v) && f == (ret > p->v)))
            ret = p->v;
        if(v == p->v)
            p = p->ch[f];
        else p = p->ch[v > p->v];
    }
    return ret;
}

int main () {
    init();
    int kase = getint();
    while(kase--) {
        int opt = getint(), x = getint();
        switch(opt) {
            case 1:insert(root, x); break;
            case 2:del(root, x); break;
            case 3:printf("%d
", sel(x)); break;
            case 4:printf("%d
", rk(x)); break;
            case 5:printf("%d
", query(x, 0)); break;
            case 6:printf("%d
", query(x, 1)); break;
        }
    }
}

但可能还是没有avl快