前言
- 最近学了基于连通性的状压DP,也就是插头DP,写了几道题,发现这DP实质上就是状压+分类讨论,轮廓线什么的也特别的神奇。下面这题把我WA到死…
HDU-5531 Efficient Tree
-
给出一个的网格图,以及相邻四联通格子之间的边权。
对于命题,如果成立,那么 ,否则
对于一颗生成树,每个点的贡献为 。这棵树的贡献为所有点的贡献之积。要求:- 最小生成树的边权和
- 所有最小生成树的贡献之和。
-
由于最大只有,考虑轮廓线DP:
- 表示当前在 这个点,轮廓线上方的格子联通情况为的边权之和
- 表示当前在 这个点,轮廓线上方的格子联通情况为的贡献之和
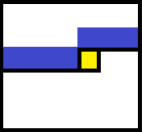
- 黄色格子就是当前考虑的点,蓝色部分就是上一次状压的 个格子
- 此处的是用最小表示法状压的,状态是长度为 的 进制数,每个位置上的值表示每一个蓝色格子在哪一个联通块里
- 这里的状压与普通插头DP有点不同,普通插头DP的状态长度是,因为多算上了中间那一条竖着的轮廓线,而这里并不用。
-
转移比较简单,只要注意两点:
- 如果当前格子上面的格子在单独一个联通块,那么这条向上的边必须选,否则就无法形成一棵联通的树。
- 如果上面的格子和左边的格子在同一个联通块就不能合并,否则构成了一个环。
AC代码
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAXN = 805, MAXM = 10;
const int HASH = 10007, NUM = 1000005;
const int mod = 1e9+7, inf = 0x3f3f3f3f;
struct node {
int w, sum;
node(int _w=0, int _sum=0):w(_w), sum(_sum){}
inline node operator +(const node &t)const {
if(w < t.w) return *this;
if(w > t.w) return t;
return node(w, (sum+t.sum)%mod);
}
inline node operator +(const int &t)const {
return node(w+t, sum);
}
inline node operator *(const int &t)const {
return node(w, 1ll*sum*t%mod);
}
};
int n, m;
int L[MAXN][MAXM], U[MAXN][MAXM];
struct HashMap {
int val[NUM], adj[HASH], pre[NUM], tot;
node f[NUM];
inline void init() {
memset(adj, -1, sizeof adj); tot = 0;
}
inline void insert(const int &x, const node &tmp) {
int u = x % HASH;
for(int i = adj[u]; ~i; i = pre[i])
if(val[i] == x) {
f[i] = f[i] + tmp; return;
}
val[++tot] = x; pre[tot] = adj[u]; adj[u] = tot; f[tot] = tmp;
}
}h[2];
int msk[MAXM], id[MAXM];
inline void decode(int x) {
for(int i = m; i; --i, x>>=3) msk[i] = x&7;
}
inline int encode(const int &m) {
int res = 0, cur = 0;
memset(id, -1, sizeof id);
id[0] = 0;
for(int i = 1; i <= m; ++i) {
if(id[msk[i]] == -1) id[msk[i]] = ++cur;
res = (res<<3)|id[msk[i]];
//注意这里不能 msk[i]=id[msk[i]], 否则改变了 msk[i]的值, dp函数中的x,y值就不对了
}
return res;
}
inline void dp(const int &i, const int &j, const int &now) {
for(int k = 1; k <= h[now^1].tot; ++k) {
decode(h[now^1].val[k]);
int x = msk[j-1], y = msk[j];
bool one = 1;
for(int l = 0; l <= m; ++l) //看是否是独立的联通块
if(l != j && msk[l] == y) { one = 0; break; }
if(!one) { //自成联通块
msk[j] = 8; //赋值为不可能出现的8
h[now].insert(encode(m), h[now^1].f[k]);
msk[j] = y;
}
if(i > 1)
h[now].insert(encode(m), (h[now^1].f[k] + U[i][j])*2);//只连左边
if(j > 1 && !one) {
msk[j] = x;
h[now].insert(encode(m), (h[now^1].f[k] + L[i][j])*2);//只连上边
msk[j] = y;
}
if(i > 1 && j > 1 && x != y) { //两边都连
for(int l = 0; l <= m; ++l) if(msk[l] == x) msk[l] = y;
h[now].insert(encode(m), (h[now^1].f[k] + L[i][j] + U[i][j])*3);
}
}
}
int main () {
int T;
scanf("%d", &T);
for(int kase = 1; kase <= T; ++kase) {
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; ++i)
for(int j = 2; j <= m; ++j)
scanf("%d", &L[i][j]);
for(int i = 2; i <= n; ++i)
for(int j = 1; j <= m; ++j)
scanf("%d", &U[i][j]);
int now = 0; h[now].init(); h[now].insert(0, node(0, 1));
for(int i = 1; i <= n; ++i)
for(int j = 1; j <= m; ++j) {
now ^= 1; h[now].init();
dp(i, j, now);
}
node ans = node(inf, 0);
for(int i = 1; i <= h[now].tot; ++i) {
bool flag = 1;
decode(h[now].val[i]);
for(int j = 1; j < m; ++j)
if(msk[j] != msk[j+1]) { flag = 0; break; }
if(flag) ans = ans + h[now].f[i];
}
printf("Case #%d: %d %d
", kase, ans.w, ans.sum);
}
}
-
我之所以WA就是因为函数里改变了的值,出来后函数里的就不对了,WA到自闭…
-
还有我的代码只用了,第位没用