题目
题目背景
传说中,南极有一片广阔的冰原,在冰原下藏有史前文明的遗址。整个冰原被横竖划分成了很多个大小相等的方格。在这个冰原上有N个大小不等的矩形冰山,这些巨大的冰山有着和南极一样古老的历史,每个矩形冰山至少占据一个方格,且其必定完整地占据方格。冰山和冰山之间不会重叠,也不会有边或点相连。以下两种情况均是不可能出现的:
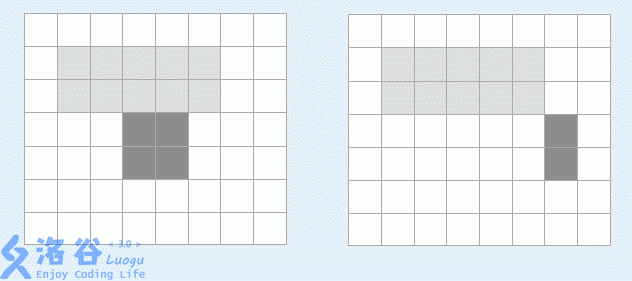
题目描述
ACM探险队在经过多年准备之后决定在这个冰原上寻找遗址。根据他们掌握的资料,在这个冰原上一个大小为一格的深洞中,藏有一个由史前人类制作的开关。而唯一可以打开这个开关的是一个占据接近一格的可移动的小冰块。显然,在南极是不可能有这样小的独立冰块的,所以这块冰块也一定是史前文明的产物。他们在想办法把这个冰块推到洞里去,这样就可以打开一条通往冰原底部的通道,发掘史前文明的秘密。冰块的起始位置与深洞的位置均不和任何冰山相邻。这个冰原上的冰面和冰山都是完全光滑的,轻轻的推动冰块就可以使这个冰块向前滑行,直到撞到一座冰山就在它的边上停下来。冰块可以穿过冰面上所有没有冰山的区域,也可以从两座冰山之间穿过(见下图)。冰块只能沿网格方向推动。
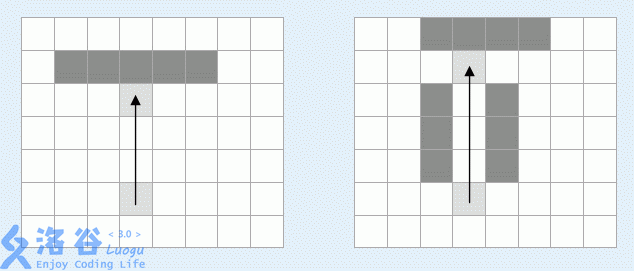
请你帮助他们以最少的推动次数将冰块推入深洞中。
输入输出格式
输入格式:输入文件第一行为冰山的个数N (1<=N<=4000),第二行为冰块开始所在的方格坐标X1,Y1,第三行为深洞所在的方格坐标X2,Y2,以下N行每行有四个数,分别是每个冰山所占的格子左上角和右下角坐标Xi1,Yi1,Xi2,Yi2
输出格式:输出文件仅包含一个整数,为最少推动冰块的次数。如果无法将冰块推入深洞中,则输出0。
输入输出样例
2 1 1 5 5 1 3 3 3 6 2 8 4
3
说明
1<=N<=4000
分析
首先,这道题就是一个找路径的问题。要用BFS是一定的。问题就是这道题有一个特殊的推法,物体知道撞到冰山才会停下。那么我们每次搜索就要判断,下一次撞到的第一个冰山是哪个。做法也就是枚举每个冰山,然后检查是否能撞到,然后用擂台来比较最接近冰块的冰山。
卡点
几个卡点:
- 如果最后没有移动到冰山别忘了输出0……
- 要分清题目当中L_U和R_D分别是什么方向上的最值。要求最大值,就要赋值为极小值,要求最小值,就要赋值极大值。
- 输出的时候,不要忘了再加上1.
程序
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int MAXN = 10000, MAXINT = 0x7FFFFFFF; 4 struct node 5 { 6 int x, y, dis, dir; 7 }; 8 queue<node> Q; 9 struct cor 10 { 11 int x,y; 12 }ice, hole, ML[MAXN], MR[MAXN]; 13 int n; 14 bool vis[MAXN << 2]; 15 int main() 16 { 17 cin >> n; 18 cin >> ice.x >> ice.y; 19 cin >> hole.x >> hole.y; 20 for (int i = 1; i <= n; i++) 21 cin >> ML[i].x >> ML[i].y >> MR[i].x >> MR[i].y; 22 Q.push((node){ice.x,ice.y,0,0}); 23 Q.push((node){ice.x,ice.y,0,1}); 24 while (!Q.empty()) 25 { 26 node temp = Q.front(); 27 Q.pop(); 28 int L_U = MAXINT, R_D = -MAXINT, LUM = 0, RDM = 0; 29 if (temp.dir) 30 { 31 for (int i = 1; i <= n; i++) 32 if (ML[i].x <= temp.x && MR[i].x >= temp.x) 33 { 34 if (ML[i].y > temp.y && ML[i].y < L_U) 35 L_U = ML[i].y, LUM = i; 36 if (MR[i].y < temp.y && MR[i].y > R_D) 37 R_D = MR[i].y, RDM = i; 38 } 39 if (LUM && !vis[LUM << 2]) 40 vis[LUM << 2] = true, Q.push((node){temp.x,L_U-1,temp.dis+1,0}); 41 if (RDM && !vis[RDM << 2|1]) 42 vis[RDM << 2|1] = true, Q.push((node){temp.x,R_D+1,temp.dis+1,0}); 43 if (temp.x == hole.x && R_D <= hole.y && hole.y <= L_U) 44 { 45 cout << temp.dis + 1 << endl; 46 return 0; 47 } 48 } 49 else 50 { 51 for (int i = 1; i <= n; i++) 52 if (ML[i].y<= temp.y && MR[i].y >= temp.y) 53 { 54 if (ML[i].x > temp.x && ML[i].x < L_U) 55 L_U = ML[i].x, LUM = i; 56 if (MR[i].x < temp.x && MR[i].x > R_D) 57 R_D = MR[i].x, RDM = i; 58 } 59 if (LUM && !vis[LUM << 2|2]) 60 vis[LUM << 2|2] = true, Q.push((node){L_U-1,temp.y,temp.dis+1,1}); 61 if (RDM && !vis[RDM << 2|3]) 62 vis[RDM << 2|3] = true, Q.push((node){R_D+1,temp.y,temp.dis+1,1}); 63 if (temp.y == hole.y && R_D <= hole.x && hole.x <= L_U) 64 { 65 cout << temp.dis + 1 << endl; 66 return 0; 67 } 68 } 69 } 70 cout << 0 << endl; 71 return 0; 72 }