近来对贝叶斯网十分感兴趣，按照博客《读懂概率图模型：你需要从基本概念和参数估计开始》给出的第一个例子，试着搭建了一个student网。
(1)点击绿F
，对条件概率表予以输入（包括两个祖先节点difficulty和intelligence，这两个节点的绿F输入将会显现在柱状图面版上，其它CPT输入则不显示在面版，仅在点击黄色闪电后自动计算得到）。
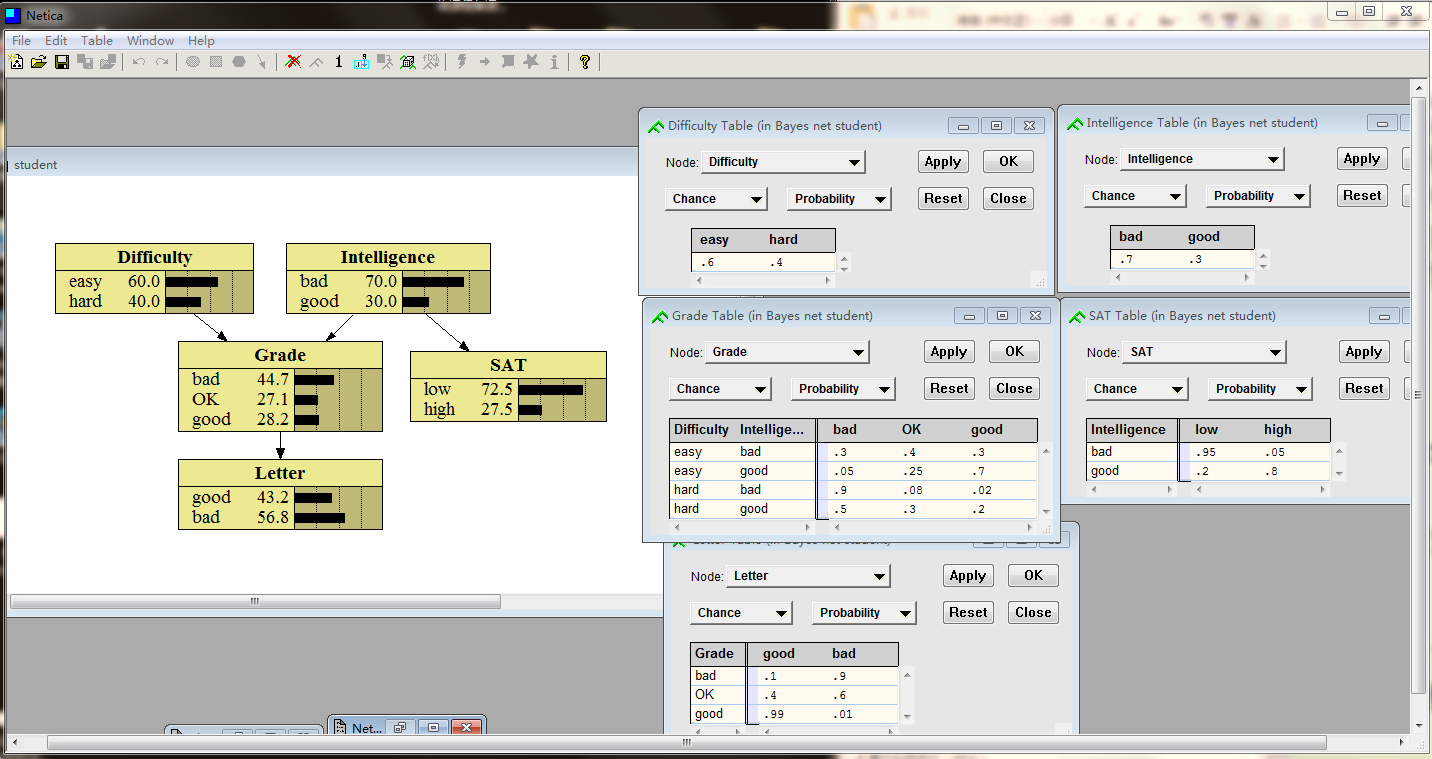
(2)现以SAT为例说明为什么p(SAT=low)=0.725：
已知先验概率：p(intelligence=bad)=0.7，p(intelligence=good)=0.3
根据CPT可知likelihood：
p(SAT=low|intelligence=bad)=0.95
p(SAT=low|intelligence=good)=0.2
p(SAT=high|intelligence=bad)=0.05
p(SAT=high|intelligence=good)=0.8
故可以计算evidence如下：
p(SAT=low)=$∑_{intelligence}$ p(SAT=low,intelligence)
=p(SAT=low,intelligence=good)+p(SAT=low,intelligence=bad)
=p(SAT=low|intelligence=good)p(intelligence=good)
+p(SAT=low|intelligence=bad)p(intelligence=bad)
=0.2*0.3+0.95*0.7=0.725
p(SAT=high)=1-p(SAT=low)=0.275
(3)现给定证据SAT=low，并将该证据嵌入到先验概率p(intelligence=bad/good)中去，求p(intelligence=bad|SAT=low)和p(intelligence=good|SAT=low)：
由(2)知p(SAT=low)=0.725
p(intelligence=bad|SAT=low)=p(intelligence=bad,SAT=low)/ p(SAT=low)
=(0.95*0.7)/0.725=0.917
p(intelligence=good|SAT=low)=1- p(intelligence=bad|SAT=low)=0.083
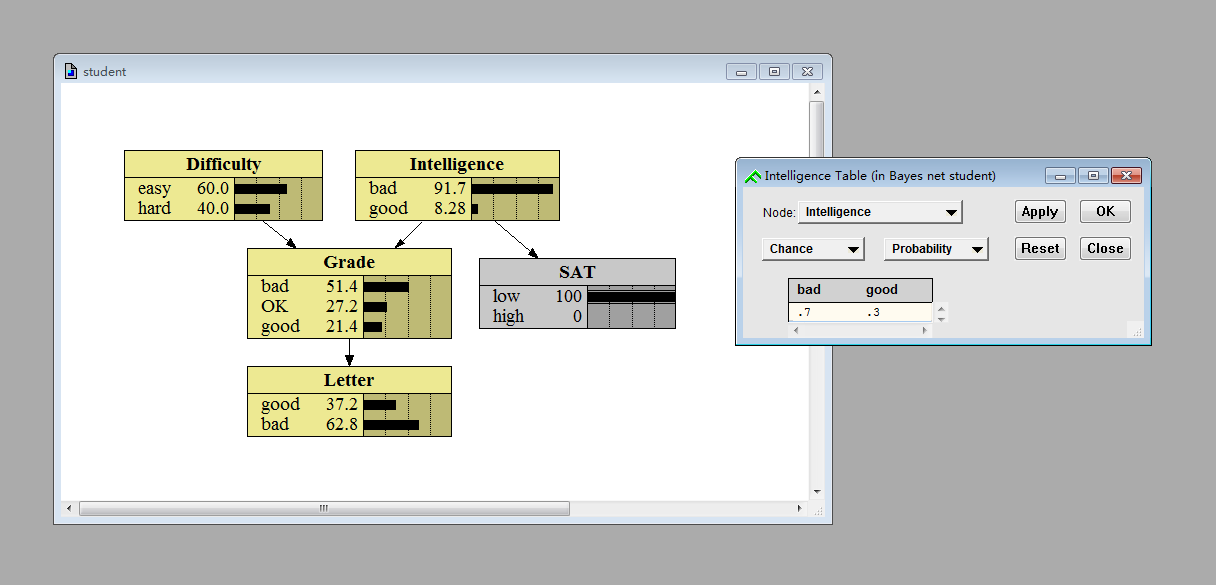
因此在给子节点SAT的值进行设定以后（变灰以后），现在显示在父节点Intelligence柱状图面板的结果实际上是嵌入证据以后的后验概率p(intelligence|SAT=low)（但是如果你点击绿F查看Intelligence可以发现表格所显示的先验概率的值p(intelligence)还是保持不变，为0.7和0.3）
(4) uncertain evidence (BRML: 3.2.1 Uncertain evidence)
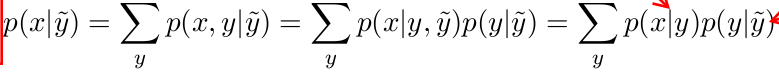
y为硬证据，y~为软证据。p(y|y~)是“硬证据确实成立”的概率。以Gibbon太太为例：
“100%确定听到报警”是硬证据（y=1），“0%确定听到报警（没听到报警）”同样是硬证据（y=0）；
“80%确定听到报警”是软证据（y~），硬证据y=1确实成立的概率p(y=1|y~)为80%，硬证据y=0确实成立的概率p(y=0|y~)=20%。
——————
在(3)里我们是将“SAT考了低分”作为证据嵌入的，此时“SAT低分”是确凿无疑的（称之为“硬证据”）。现在仍然以SAT成绩和智力水平为例，当我不知道我的智力水平，且SAT成绩还没出来，但是我刚刚考完SAT，对自己考了多少分有个大概的估计（以下图为例：我仅有33.7%的把握我SAT考的不错），那么这个“不确定成绩”也是可以作为证据嵌入的，称之为“软证据”。现在我们希望计算嵌入软证据后的后验概率p(intelligence|SAT~)。
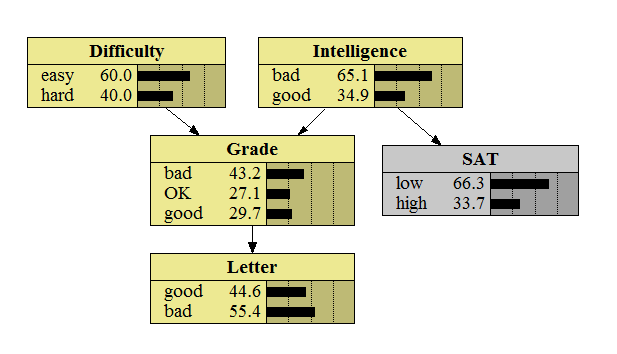
软证据如下：
66.3%确定SAT=low——p(SAT=low|SAT~)=0.663
33.7%确定SAT=high——p(SAT=high|SAT~)=0.337
由上面的公式：
p(intelligence=bad|SAT~)=$∑_{SAT}$ p(intelligence=bad|SAT)p(SAT|SAT~)
= p(intelligence=bad|SAT=low)p(SAT=low|SAT~)
+ p(intelligence=bad|SAT=high)p(SAT=high|SAT~)
=0.917*α+0.127(1-α)
=0.917*0.663+0.127*0.337
=0.651
（其中α=0.663，为“SAT考低分的确信程度”）
（红色部分即(3)中算出的结果，绿色部分我还没有算，可以用类似的方法手算得出，也可以简单地在SAT面板上将high的柱状图拉到100%再看intelligence面板上bad的显示值）
2018.9.20
by 悠望南山