[BZOJ 3894]文理分科

Description

题库链接

给你一个 (n imes m) 的网格，每个网格代表一个学生。一个学生 ((i,j)) 选文，那么可以获得 (a_{i,j}) 的愉♂悦值；若选理那么可以获得 (b_{i,j}) 的愉♂悦值。

如果这个人和他四连通的所有人选择是一样的，那么可以额外获得 (ea_{i,j}) （或 (eb_{i,j}) ，取决于均选文或选理）点愉♂悦值。

求愉悦值总和最大。

(1leq n,mleq 100)

Solution

建立最小割模型，对于相邻的 (5) 个节点，我们建立新的节点 (x,y) ，如图（对于一个五连通块来说）：

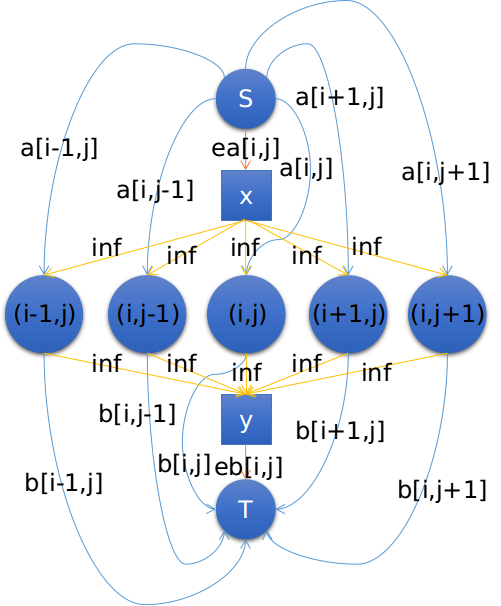
如果割掉的是 (a) 边，那么表示选理，割掉的是 (b) 边，那么表示选文。

若割掉 (ea) 边，表示不全选文，若割掉 (eb) 边，表示不全选理。

可以用假设法证明图的正确性。

Code

#include <bits/stdc++.h>
using namespace std;
const int N = 140000+5, inf = ~0u>>1;
const int w1[4] = {-1, 1, 0, 0};
const int w2[4] = {0, 0, -1, 1};

int n, m, a[105][105], b[105][105], ea[105][105], eb[105][105];
int hab[105][105], hea[105][105], heb[105][105];
struct tt {int to, next, cap; }edge[N<<1];
int path[N], top, S = N-2, T = N-1, cnt, ans;
int sta[N], dist[N], cur[N];
queue<int>Q;

void add(int u, int v, int c) {
    edge[++top] = (tt){v, path[u], c}, path[u] = top;
    edge[++top] = (tt){u, path[v], 0}, path[v] = top;
}
bool bfs() {
    memset(dist, -1, sizeof(dist)); dist[S] = 1; Q.push(S);
    while (!Q.empty()) {
        int u = Q.front(); Q.pop();
        for (int i = path[u], v; ~i; i = edge[i].next)
            if (dist[v = edge[i].to] == -1 && edge[i].cap) {
                dist[v] = dist[u]+1; Q.push(v);
            }
    }
    return dist[T] != -1;
}
int dinic() {
    int tolflow = 0;
    while (bfs()) {
        memcpy(cur, path, sizeof(cur)); int u = S, top = 0;
        while (true) {
            if (u == T) {
                int minflow = inf, loc;
                for (int i = 1; i <= top; i++) if (edge[sta[i]].cap < minflow) loc = i, minflow = edge[sta[i]].cap;
                for (int i = 1; i <= top; i++) edge[sta[i]].cap -= minflow, edge[sta[i]^1].cap += minflow;
                tolflow += minflow, u = edge[sta[loc]^1].to, top = loc-1;
            }
            for (int v, &i = cur[u]; ~i; i = edge[i].next)
                if (dist[v = edge[i].to] == dist[u]+1 && edge[i].cap) {
                    sta[++top] = i, u = v; break;
                }
            if (cur[u] == -1) {
                dist[u] = -1; if (top == 0) break;
                u = edge[sta[top--]^1].to;
            }
        }
    }
    return tolflow;
}
void work() {
    memset(path, top = -1, sizeof(path));
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) scanf("%d", &a[i][j]);
    for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) scanf("%d", &b[i][j]);
    for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) scanf("%d", &ea[i][j]);
    for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) scanf("%d", &eb[i][j]);
    for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) hab[i][j] = ++cnt;
    for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) hea[i][j] = ++cnt;
    for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) heb[i][j] = ++cnt;
    for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) add(S, hab[i][j], a[i][j]);
    for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) add(hab[i][j], T, b[i][j]);
    for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) add(S, hea[i][j], ea[i][j]);
    for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) add(heb[i][j], T, eb[i][j]);
    for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) {
        add(hea[i][j], hab[i][j], inf);
        for (int k = 0; k < 4; k++) if (hab[i+w1[k]][j+w2[k]] != 0)
            add(hea[i][j], hab[i+w1[k]][j+w2[k]], inf);
    }
    for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) {
        add(hab[i][j], heb[i][j], inf);
        for (int k = 0; k < 4; k++) if (hab[i+w1[k]][j+w2[k]] != 0)
            add(hab[i+w1[k]][j+w2[k]], heb[i][j], inf);
    }
    for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++)
        ans += a[i][j]+b[i][j]+ea[i][j]+eb[i][j];   
    printf("%d
", ans-dinic());
}
int main() {work(); return 0; }