Description
辣鸡蒟蒻SOL是一个傻逼,他居然觉得数很萌!
今天他萌上了组合数。现在他很想知道simga(C(n,i))是多少;其中C是组合数(即C(n,i)表示n个物品无顺序选取i个的方案数),i取从0到n所有偶数。
由于答案可能很大,请输出答案对6662333的余数。
Input
输入仅包含一个整数n。
Output
输出一个整数,即为答案。
Sample Input
3
Sample Output
4
Hint
对于20%的数据,n <= 20;
对于50%的数据,n <= 1000;
对于100%的数据,n <= 1 000 000 000 000 000 000 (10^18)
题解
1、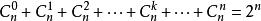
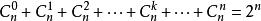
2、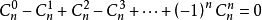
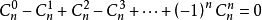
3、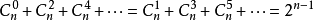
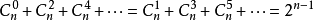
证明:由当$a = b = 1$时,代入二项式定理可证明$1$式;当$a = -1$,$b = 1$时代入二项式定理可证明$2$式;代入$a = 1$,$b = -1$可得到另一个意义相同的式子;$(1式+2式) over 2$可证明$3$式。
1 //It is made by Awson on 2017.10.12 2 #include <set> 3 #include <map> 4 #include <cmath> 5 #include <ctime> 6 #include <cmath> 7 #include <stack> 8 #include <queue> 9 #include <vector> 10 #include <string> 11 #include <cstdio> 12 #include <cstdlib> 13 #include <cstring> 14 #include <iostream> 15 #include <algorithm> 16 #define LL long long 17 #define Min(a, b) ((a) < (b) ? (a) : (b)) 18 #define Max(a, b) ((a) > (b) ? (a) : (b)) 19 #define sqr(x) ((x)*(x)) 20 using namespace std; 21 const int MOD = 6662333; 22 23 int quick_pow(int a, LL b) { 24 int sum = 1; 25 while (b) { 26 if (b&1) sum = (LL)sum*a%MOD; 27 b >>= 1; 28 a = (LL)a*a%MOD; 29 } 30 return sum; 31 } 32 void work() { 33 LL n; 34 scanf("%lld", &n); 35 printf("%d ", quick_pow(2, n-1)); 36 } 37 int main() { 38 work(); 39 return 0; 40 }
