比赛链接:http://codeforces.com/contest/1180
Problem A
题意:给出n,问方块数。看图理解。。。
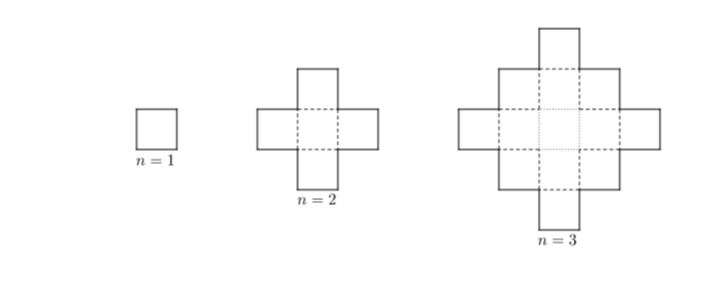
Solution:
找一找规律就可以了,发现方块数为2n*(n-1)+1
Code:
#include<bits/stdc++.h>
using namespace std;
int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int main(){
int n=read();
printf("%d
",2*n*n-2*n+1);
return 0;
}
Problem B
题意:给你一个序列,你可以把其中任意个元素变成它的相反数-1,即:(a_i:-a_i-1),求乘积最大的方案
Solution:
显然对尽可能多的非负数执行这个操作是最优的,同时我们必然能使这个最大乘积为非负数
同时对于两个非负数(a,b(b>a))来说,((a+1)b>a(b+1))
所以我们就只需要将序列中最小的负数执行操作后的值与最大的非负数比较大小就行了
Code:
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+1;
int n,_minus,add,a[N];
int maxm,maxa=-1,idm,ida;
int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int main(){
n=read();
for(int i=1;i<=n;i++){
a[i]=read();
a[i]>=0?++add:++_minus;
if(a[i]>=0&&a[i]>maxa) ida=i,maxa=a[i];
if(a[i]<0&&a[i]<maxm) idm=i,maxm=a[i];
}int f1=_minus%2,f2=add%2;
if(f1==f2){
for(int i=1;i<=n;i++)
printf("%d ",a[i]<0?a[i]:-a[i]-1);
return 0;
}
if(_minus==1&&!add){
printf("%d ",-a[1]-1);
return 0;
}
if(f1!=f2){
int id,flag=0;
if(-maxm-1>maxa) id=idm;
else id=ida,flag=1;
for(int i=1;i<id;i++)
printf("%d ",a[i]<0?a[i]:-a[i]-1);
printf("%d ",flag?a[id]:-a[id]-1);
for(int i=id+1;i<=n;i++)
printf("%d ",a[i]<0?a[i]:-a[i]-1);
}
}
Problem C
题意:给你一个序列,每次操作取出序列前两个元素(a,b),将较大元素放在序列首位,较小元素放在序列末尾,有m次询问,每次询问你第x次操作取出的是哪两个元素
Solution:
显然,当序列中的最大元素为首位时,所有跟它比较的元素都会被踢到队尾,形成循环,而最大元素替换到队首最多需要n-1次操作,则我们可以模拟最大元素替换到队首之前的所有操作,之后的操作则可以根据循环O(1)算出
Code:
#include<bits/stdc++.h>
#define ll long long
#define mp make_pair
#define fir first
#define sec second
using namespace std;
const int N=1e5+1;
int n,m,maxn;
int head,cnt,tail,q[N*31];
pair<int,int> u[N];
ll read(){
ll x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
int main(){
n=read(),m=read();
for(int i=1;i<=n;i++){
q[++tail]=read();
if(q[i]>maxn) maxn=q[i];
}head=1;
while(1){
int x=q[head],y=q[head+1];
u[++cnt]=mp(x,y);
if(x==maxn) break;
if(x>y) q[head+1]=q[head++],q[++tail]=y;
else ++head,q[++tail]=x;
}
for(int i=1;i<=m;i++){
ll x=read();
if(x<=cnt) printf("%d %d
",u[x].fir,u[x].sec);
else printf("%d %d
",maxn,q[head+1+(x-cnt)%(n-1)]);
}
return 0;
}
Problem D
题意:给定一个n*m的矩阵,一开始你在(1,1);每次移动时,设你所在点为(x,y),你可选取任意二元组(dx,dy),移动到(x+dx,y+dy)点上,但每次选取的二元组(dx,dy)不能为之前用过的。现在问是否有一种方案使你刚好经过每个点一次,如果有,按先后顺序输出到达的点,否则输出-1。
Solution:
这是一道构造题。考虑从(1,1)和(n,m)两个点依次反向之字形往返跳跃,正确性易证,详见代码(因为不是很好描述)
Code:
#include<bits/stdc++.h>
#define mp make_pair
using namespace std;
const int N=1e6+1;
int n,m,add1=1,add2=-1;
int nx,ny,mx,my,flag;
int read(){
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)){if(ch=='-')f=-1;ch=getchar();}
while(isdigit(ch)){x=x*10+ch-48;ch=getchar();}
return x*f;
}
void ins(int opt){
if(!opt){
printf("%d %d
",nx,ny);
if(nx+add1>n||nx+add1<1) ++ny,add1=-add1;
else nx+=add1;
}else{
printf("%d %d
",mx,my);
if(mx+add2<1||mx+add2>n) --my,add2=-add2;
else mx+=add2;
}
}
int main(){
n=read(),m=read();
nx=ny=1,mx=n,my=m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
ins(flag),flag^=1;
return 0;
}