题目

输入格式
数据的第1行为两个整数N和E,以空格分隔,分别表示森林中的景点数和连接相邻景点的路的条数。 第2行包含两个整数C和M,以空格分隔,分别表示初始时聪聪和可可所在的景点的编号。 接下来E行,每行两个整数,第i+2行的两个整数Ai和Bi表示景点Ai和景点Bi之间有一条路。 所有的路都是无向的,即:如果能从A走到B,就可以从B走到A。 输入保证任何两个景点之间不会有多于一条路直接相连,且聪聪和可可之间必有路直接或间接的相连。
输出格式
输出1个实数,四舍五入保留三位小数,表示平均多少个时间单位后聪聪会把可可吃掉。
输入样例
【输入样例1】
4 3
1 4
1 2
2 3
3 4
【输入样例2】
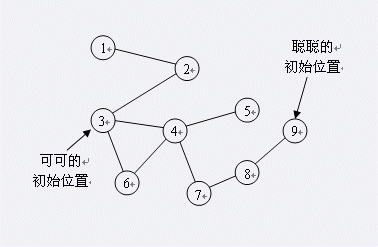
9 9
9 3
1 2
2 3
3 4
4 5
3 6
4 6
4 7
7 8
8 9
输出样例
【输出样例1】
1.500
【输出样例2】
2.167
提示
【样例说明1】
开始时,聪聪和可可分别在景点1和景点4。
第一个时刻,聪聪先走,她向更靠近可可(景点4)的景点走动,走到景点2,然后走到景点3;假定忽略走路所花时间。
可可后走,有两种可能:
第一种是走到景点3,这样聪聪和可可到达同一个景点,可可被吃掉,步数为1,概率为 。
第二种是停在景点4,不被吃掉。概率为 。
到第二个时刻,聪聪向更靠近可可(景点4)的景点走动,只需要走一步即和可可在同一景点。因此这种情况下聪聪会在两步吃掉可可。
所以平均的步数是1* +2* =1.5步。
对于所有的数据,1≤N,E≤1000。
对于50%的数据,1≤N≤50。
题解
讲实在的不难写,但是概率这种玩意写起来总是很蛋疼【蒟蒻跪倒】
由于聪聪的走法是唯一的、可求的,我们不妨令(p[i][j])表示聪聪在i号点,可可在j号点时聪聪的下一步位置
由于(n<=1000),我们可以用SPFA求出从每个点u出发所有点到达该点最短路的上一个节点,即为每个点出发到u点的下一个节点
现在我们有了p[][],就很好求了
我们设(f[i][j])表示聪聪在i号点,可可在j号点的期望步数
若(i == j),聪聪可可在一起,(f[i][j] = 0)
若(p[i][j] == j)或(p[p[i][j]][j]==j),可以一次性走到,(f[i][j] = 1)
否则令(t = p[p[i][j]][j]),枚举j的邻点v,(f[i][j]=frac{f[t][j] + sum{f[t][v]}}{degree_j + 1} + 1)
记忆化搜索解决
#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#define LL long long int
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
using namespace std;
const int maxn = 1005,maxm = 2000005,INF = 1000000000;
inline int read(){
int out = 0,flag = 1; char c = getchar();
while (c < 48 || c > 57) {if (c == '-') flag = -1; c = getchar();}
while (c >= 48 && c <= 57) {out = (out << 3) + (out << 1) + c - '0'; c = getchar();}
return out * flag;
}
int p[maxn][maxn],isc[maxn][maxn],d[maxn],vis[maxn],pre[maxn],de[maxn];
double f[maxn][maxn];
int h[maxn],ne = 2,n,m,cc,kk;
struct EDGE{int to,nxt;}ed[maxm];
void build(int u,int v){
de[u]++; de[v]++;
ed[ne] = (EDGE){v,h[u]}; h[u] = ne++;
ed[ne] = (EDGE){u,h[v]}; h[v] = ne++;
}
queue<int> q;
void spfa(int S){
REP(i,n) d[i] = INF,vis[i] = false,pre[i] = 0;
d[S] = 0; q.push(S); int u;
while (!q.empty()){
u = q.front(); q.pop();
vis[u] = false;
Redge(u) if (d[to = ed[k].to] > d[u] + 1 || (d[to] == d[u] + 1 && u < pre[to])){
d[to] = d[u] + 1; pre[to] = u;
if (!vis[to]) q.push(to),vis[to] = true;
}
}
REP(i,n) if (i != S) p[i][S] = pre[i];
}
double dp(int u,int v){
if (isc[u][v]) return f[u][v];
isc[u][v] = true;
if (u == v) return f[u][v] = 0;
if (p[u][v] == v) return f[u][v] = 1;
if (p[p[u][v]][v] == v) return f[u][v] = 1;
int t = p[p[u][v]][v]; double ans = dp(t,v);
Redge(v) ans += dp(t,ed[k].to);
return f[u][v] = ans / (de[v] + 1) + 1;
}
int main(){
n = read(); m = read(); cc = read(); kk = read();
while (m--) build(read(),read());
REP(i,n) spfa(i);
printf("%.3lf
",dp(cc,kk));
return 0;
}