Codeforces 103B. Cthulhu 并查集运用

题目链接；

题面：

...Once upon a time a man came to the sea. The sea was stormy and dark. The man started to call for the little mermaid to appear but alas, he only woke up Cthulhu...

Whereas on the other end of the world Pentagon is actively collecting information trying to predict the monster's behavior and preparing the secret super weapon. Due to high seismic activity and poor weather conditions the satellites haven't yet been able to make clear shots of the monster. The analysis of the first shot resulted in an undirected graph with n vertices and m edges. Now the world's best minds are about to determine whether this graph can be regarded as Cthulhu or not.

To add simplicity, let's suppose that Cthulhu looks from the space like some spherical body with tentacles attached to it. Formally, we shall regard as Cthulhu such an undirected graph that can be represented as a set of three or more rooted trees, whose roots are connected by a simple cycle.

It is guaranteed that the graph contains no multiple edges and self-loops.

Input

The first line contains two integers — the number of vertices n and the number of edges m of the graph (1 ≤ n ≤ 100, 0 ≤ m ≤ ).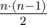

Each of the following m lines contains a pair of integers x and y, that show that an edge exists between vertices x and y(1 ≤ x, y ≤ n, x ≠ y). For each pair of vertices there will be at most one edge between them, no edge connects a vertex to itself.

Output

Print "NO", if the graph is not Cthulhu and "FHTAGN!" if it is.

题意：给定一个图，如果这个图可以被视为大于3的有根树其中它们的根构成一个环，就输出FHTAGN，否则输出NO。

解题思路：首先，这个图被保证不存在自环和平行边。那么如果存在一个环，这个环的长度必定大于3，即必定能够拆分环形成三棵以上的树。因此，只需要判断给定的图中是否只存在一个环，且整个图是连通的（因为没判断这个wa了很多发）。到这里自然就想到了用并查集判断无向图中是否存在环。

AC代码：

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 200;

int par[MAXN];   

void init()
{
    for(int i=0; i<MAXN; i++)
    {
        par[i] = i;
    }
}

int findd(int x)
{
    if(par[x]==x)
        return x;
    else
        return par[x] = findd(par[x]); 
}

void unite(int x,int y)
{
    x = findd(x);
    y = findd(y);
    if(x == y)
        return;
    else
    {
        par[x] = y;
    }
}

//判断x和y是否属于同一集合
bool same(int x, int y)
{
    return findd(x)==findd(y);
}

int main()
{
    int n,m;
    while(~scanf("%d %d",&n,&m))
    {
        int a,b;
        int circlecnt = 0;
        init();
        for(int i=0; i<m; i++)
        {
            scanf("%d %d",&a,&b);
            if(same(a,b))
                circlecnt++;    //环数
            else
                unite(a,b);
        }
        int setcnt = 0;
        for(int i=1; i<=n; i++)
            if(par[i] == i)
                setcnt++;    //集合数
        if(circlecnt==1 && setcnt==1)
            printf("FHTAGN!
");
        else
            printf("NO
");
    }
    return 0;
}