机器学习基本概念简介
1. 浅析机器学习
机器学习可以约等于找一个函数的能力,具备函数能力后可以做很多事情。例如:语音识别(1)、影像辨识(2)、下围棋(3)
(1)

(2)

(3)
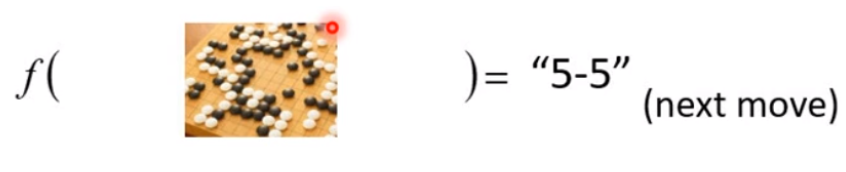
2. 不同类型的函数:
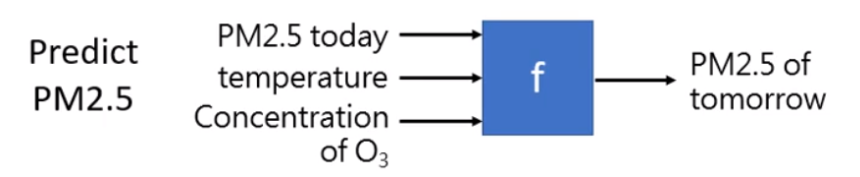
(1)Regression:输出是一个数值。例如:预测明天的PM2.5的量
(2)Classfication:需要机器做的是选择题,我们预先准备一些选项(classes),机器从预设选项中选择一个当作输出。例如:垃圾邮件的侦测

(3)Structured Learning:create something with structure(image,document)产生有结构的事物。通俗来讲,让机器学会创造。
3-1. 如何找到目标函数(以Youtube点阅人数预测为例)

y:预测2月26日频道的总观看人数。(feature)
x1:2月25日频道的总观看人数。(feature)
w (weight)and b(bias):未知参数(想要从数据中获取的参数)
y = b+wx1 叫做model(模型)
3-2. 从训练数据定义损失函数(Loss)
(1)Loss is a function of parameters | L(b,w)| 损失函数是与b与w相关的函数 | 即把b和w设置为未知参数的时候,这组数值的好坏的衡量
(2)举例说明Loss(Label表示正确数值)
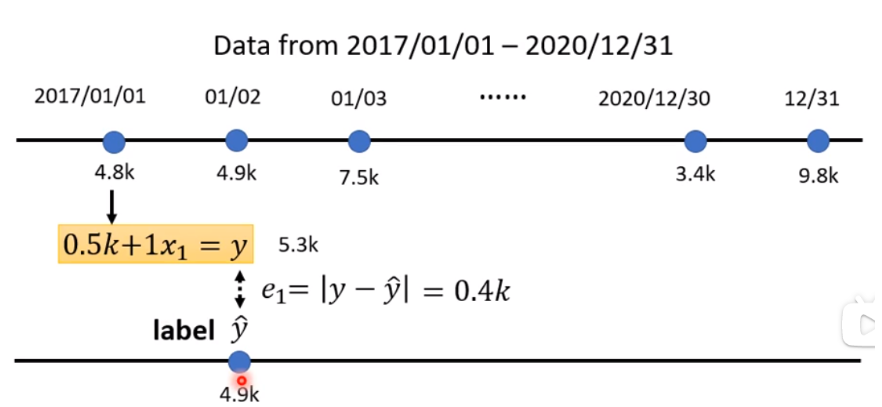
依次类推,计算每天相较第二天的训练误差。
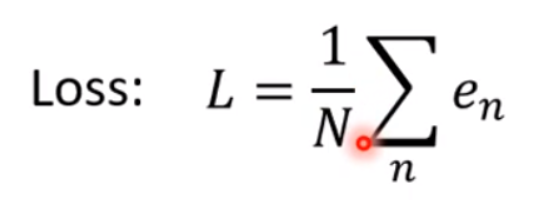
(3)平均绝对误差和均方误差以及交叉熵计算法

(4)Loss的等高线分布图(Error Surface:误差曲面)

3-3 Optimization:最优解问题
1.找出效果最好的一组w和b让Loss的值最小。
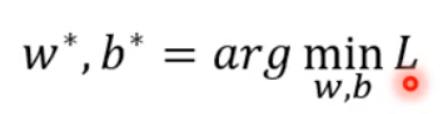
2.Gradient Descent(梯度下降)
(1)首先假设未知参数只有一个:w

(2)获取不同的w与Loss的关系
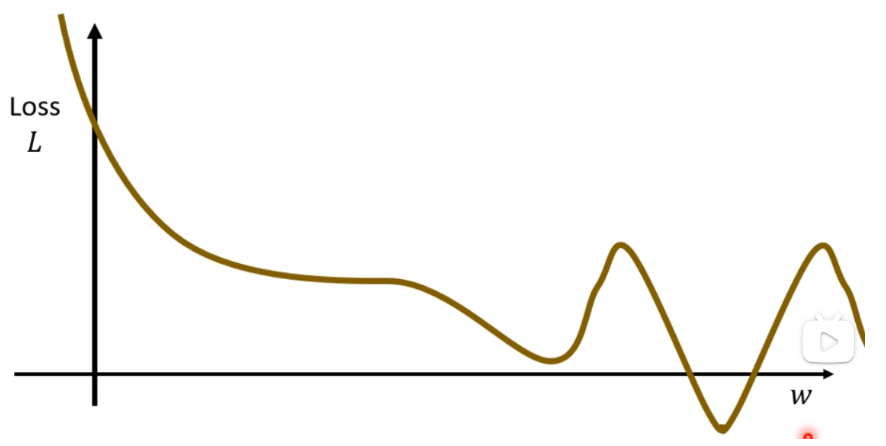
(3)找到一个W使得Loss的值最小,首先随机挑选一个W0
(4)计算w = w0 这一点的切线斜率
(5)若w = 负值 —> 增加w
(6)若w = 正数 —> 减小w
(7)增加和减小的大小取决于该点斜率的大小和学习率的大小(hyperparameters表示人为设定的数值)

(8)移动
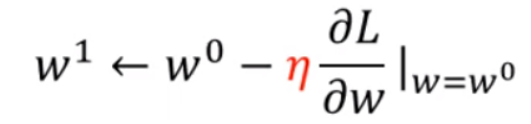
(9)停下的两种原因
人为设置了参数更新
计算得到的微分为0,参数不再移动
(10)存在问题:上述例子很显然可以发现梯度下降找到的不是最优的w,不是最优解的数值叫做local minima(局部最小值),真正的最优解是global minima(全局最小值)
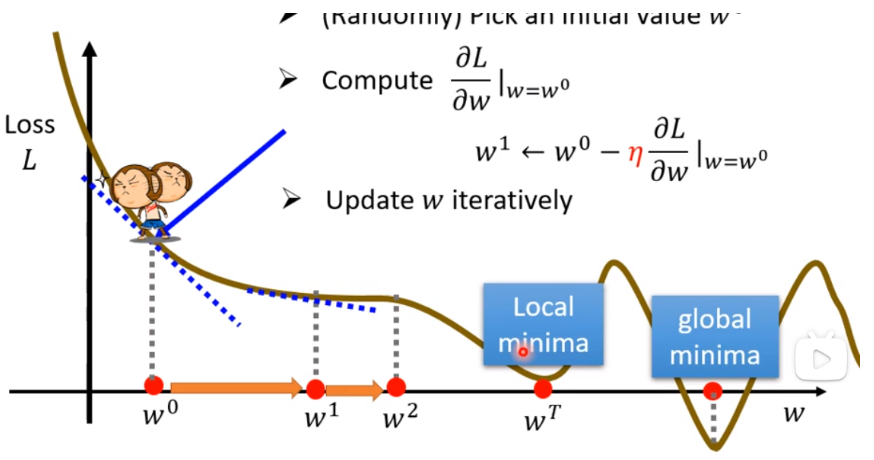
(11)拓展:local minima不是Gradient descent真正的问题
3.双参数引入


4.接下来的问题
我们需要知道的是未来的观看次数,所以要使用上述得到的函数获取未来的观看次数。

(1)分析结果
横轴代表时间,纵轴代表观看的人数
真实数据每隔七天就会有两天特别低

(2)修改模型(增加数据天数)
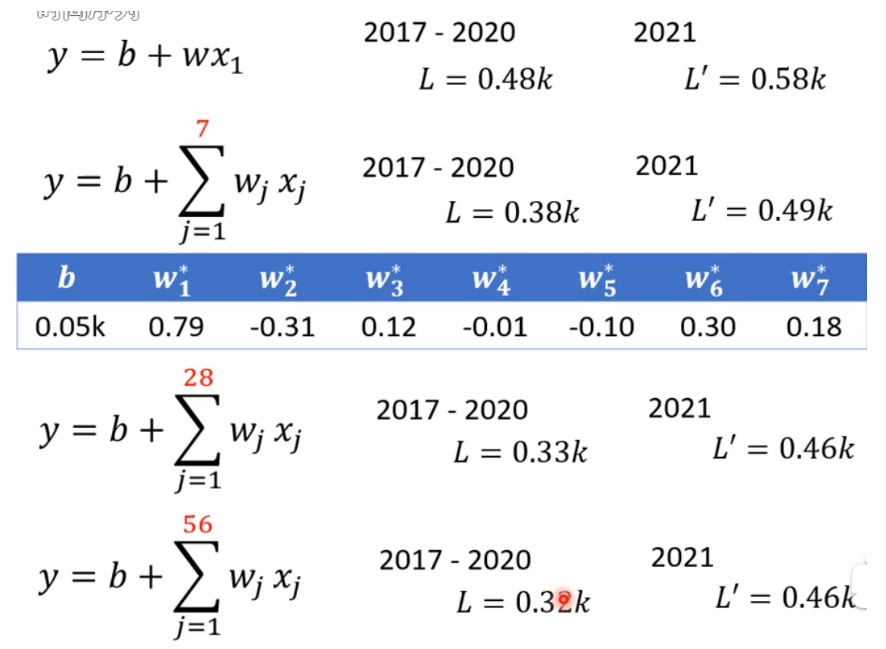
以上所用的模型统称为Linear models