剑指Offer:矩形覆盖【N1】
题目描述
我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
题目思考
大矩形是由单元块(1*2)填充的,但是大矩形不是一下生成的,而是由比他小的矩形通过添加单元块生成的,添加的策略只能是两种
- 第一,小矩形右侧添加竖状单元块,要求,小矩形比大矩形小一个单位。
- 第二,小矩形右侧添加横状单元块,要求,小矩形比大矩形少两个单位。
这依然是斐波那契数列变形题,经典的动态规划题目,按照斐波那契数列特点求解,每个子问题,即不同长度的小矩形方法数,求解一次,存在存储表中,下次遇到后直接取用即可。
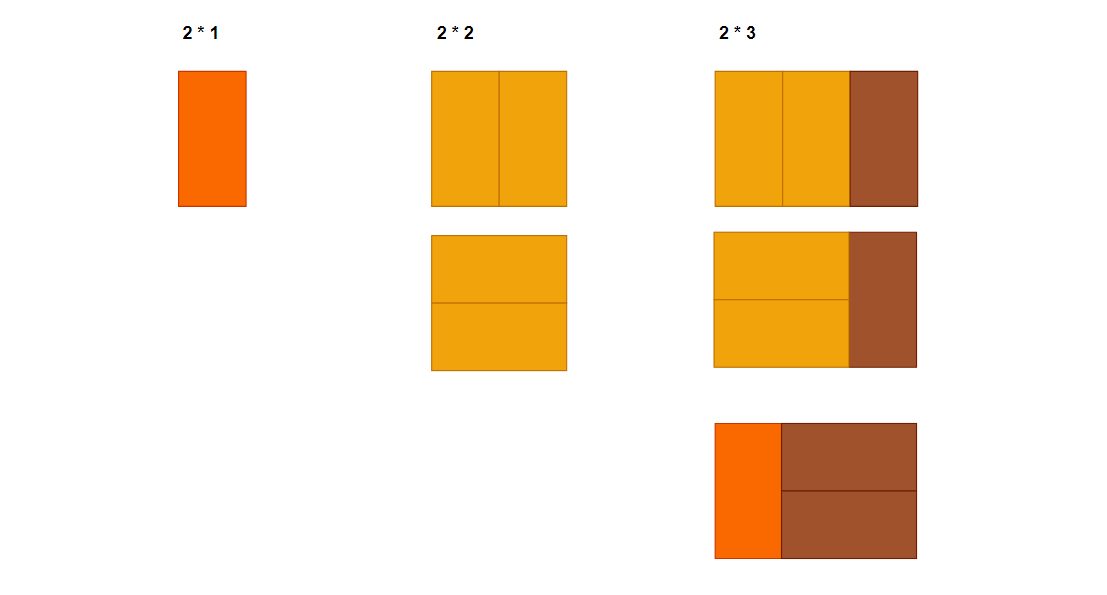
Java题解
public class RectCover {
public static int RectCover(int n) {
if (n <= 2)
return n;
int[] dp = new int[n];
dp[0] = 1;
dp[1] = 2;
for (int i = 2; i < n; i++)
dp[i] = dp[i - 1] + dp[i - 2];
return dp[n - 1];
}
public static void main(String[] args) {
System.out.println(RectCover(3));
}
}