矩阵我个人理解就是一堆数据放在一块儿排列整齐,当然正规一点说就是m行n列的数据构成。在编程中一般采用数组对其进行存储,但矩阵中的某些特殊矩阵里,有时会出现很多数据相等或者存有很多0只有某几个位置为别的数据,那么这类矩阵我们在用数组存储的时候就会感觉比较的浪费空间,那么会对一些特殊矩阵进行压缩存储。
常见的能够压缩存储的矩阵有对称矩阵和稀疏矩阵,今天主要说说对称矩阵的压缩存储。先来说说什么是对称矩阵,相信大家都很熟悉,对于一个矩阵如果它的行和列相等并且矩阵中的数据是关于对角线对称的,那么我们称这样的矩阵为对称矩阵,拿公式来说就是:A[i][j] = A[j][i](0<=i<=N-1&&0<=j<=N-1)。
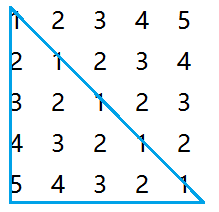
那么对于这样的对称矩阵我就只需要存储它的一个上三角或者下三角就足够,没必要对另一部分重复的数据存储。
一维数组开辟多大:
观察上面的对称矩阵,如果我要存储下三角,那么在类中给一位数组开辟的大小是多少呢?可以看到下三角第一行为一个元素,往下依次递增,直到最后一行N个元素,可以发现就是等差数列求和的问题,那么来计算:(1+5)*5/2=15,因此用来存储矩阵的一位数组开辟上15个空间的大小,这样相对于之前能够节省接近一半的存储空间。
对称矩阵和压缩存储的对应关系:
因为是存储下三角,所以是把矩阵中元素A[i][j](i>=j)存放到数组Array中。那么在这里看一下两者的对应关系。
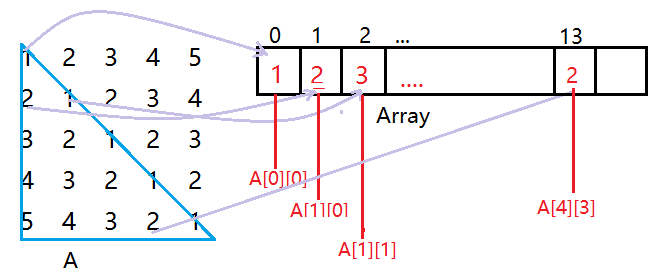
上图给出了矩阵中部分元素在一位数组中的存储位置也就是索引,那么怎么确定其在数组中的索引呢,其实这仅仅是一个数学问题也比较简单,我们来看看在Array[13]位置存储的那个元素2,它在矩阵中的位置为A[4][3],那么我们放眼到上图中的那个下三角,这个2的上面正好有4行,那么上面的元素的个数又是一个等差求和(1+4)*4/2=10,在加上它的列数3结果就是13.所以可以列出公式为:SymmetricMatrix[i][j] == Array[i*(i+1)/2+j],SymmetricMatrix代表我们的对称矩阵。
看代码说话:
构造这样的一个对称矩阵类时,需要两个成员变量,一个是用来存放矩阵的一位数组_arr,一个是一位数组的大小_size.下面是构造函数:
SymmetricMatrix(T *arr, int N)
:_size(N*(N + 1) / 2)
{
assert(arr);
arr = new T[_size];
int idex = 0;
for (int i = 0; i < N; ++i)
{
for (int j = 0; j < N; ++j)
{
if (i >= j && idex<_size)
{
_arr[idex++] = arr[i*N + j];
}
}
}
}
其实整体代码还是比较简单的,在类中还要重载它的输出操作符,思路就是根据矩阵的i和j计算出一位数组中的索引然后输出就可以了,当然下三角的是i>=j的,所以如果循环中如果i<j的时候需要进行一次交换。
以下为整体代码:
template<typename T>
class SymmetricMatrix
{
public:
SymmetricMatrix(T *arr, int N)
:_size(N*(N + 1) / 2)
{
assert(arr);
arr = new T[_size];
int idex = 0;
for (int i = 0; i < N; ++i)
{
for (int j = 0; j < N; ++j)
{
if (i >= j && idex<_size)
{
_arr[idex++] = arr[i*N + j];
}
}
}
}
T Access(size_t _row,size_t _col)const
{
if (_row < _col)
{
swap(_row, _col);
}
return _arr[_row*(_row + 1) + _col];
}
template<typename T>
friend ostream& operator<<(ostream& _cout, const SymmetricMatrix<T> sm)
{
size_t N = sqrt((long double)sm._size * 2);
for (size_t i = 0; i < N; ++i)
{
for (size_t j = 0; j < N; ++j)
{
_cout << sm.Access(i, j) << " ";
}
_cout << endl;
}
return _cout;
}
private:
T *_arr;
int _size;
};
文章作者:Mr_listening,博客地址:http://www.cnblogs.com/MrListening/