前序(废话)
因为对考研分数没信心,博主毕业前也尝试了找工作。有尝试就知道自己不足,发现自己还是太弱了,技术栈不行,算法也不行。
虽然最后考研没录上一志愿,但是可以给自己三年时间来慢慢打磨技术、沉淀一下。痛定思过,决定有时间就一天一道LeetCode。btw:希望三年能坚持下来
题目
给定一个整数数组 nums,返回区间和在 [lower, upper] 之间的个数,包含 lower 和 upper。
区间和 S(i, j) 表示在 nums 中,位置从 i 到 j 的元素之和,包含 i 和 j (i ≤ j)。
说明:
最直观的算法复杂度是 O(n2) ,请在此基础上优化你的算法。
示例:
输入: nums = [-2,5,-1], lower = -2, upper = 2,
输出: 3
解释: 3个区间分别是: [0,0], [2,2], [0,2],它们表示的和分别为: -2, -1, 2。
题解
由于这是第一道自己刷的题,一随机还随机了一道困难题,看了两天终于看懂了
这道题有好几种解法,这里主要介绍一个博主自己写的暴力法和博客园的标准答案归并排序法
思路一:暴力遍历
暴力遍历很简单,就是使用两层for循环遍历所有可能的S(i,j)。注:不要忘记一个元素满足条件的情况
当然这里有个小坑 sum累计和需要使用long,如若使用int,当两个极大的int相加会溢出
代码
class Solution {
public static int countRangeSum(int[] nums, int lower, int upper) {
int length = nums.length; //记录数组长度
int count = 0; //统计符合要求区间个数
int j; //S(i,j)中的j
int i; //S(i,j)中的i
for(j=0;j<length;j++){ //j可以取到数组所有的元素 固遍历
if(nums[j]>=lower&&nums[j]<=upper) //在j遍历过程中,看是否有单个元素符合lower-upper要求
count++;
long sum=nums[j]; //计算累计和
for(i=j-1;i>=0;i--){ //将i从j前一个元素遍历、计算累计和
sum += nums[i];
if(sum>=lower&&sum<=upper) //满足条件 count++
count++;
}
}
return count;
}
}
思路二:归并排序法
归并排序法是博客园官方解答中的解法一,u1s1这个解法粗看上去,还是有难度的,我看了几遍答案,第二天看了其他人的题解解释才弄懂
首先我们先看一下官方的题解和代码

其实官方题解给的导入例子:给两个升序排列数组,找出符合的下标对。还是很容易理解的
但是突然来了句原问题就迎刃而解了,属实给我整懵了。找了好久网上的解释,参考了一下大佬的解释(https://leetcode-cn.com/problems/count-of-range-sum/solution/shuo-ming-yi-xia-guan-fang-gui-bing-pai-xu-by-sing/)才终于搞懂官方的意思
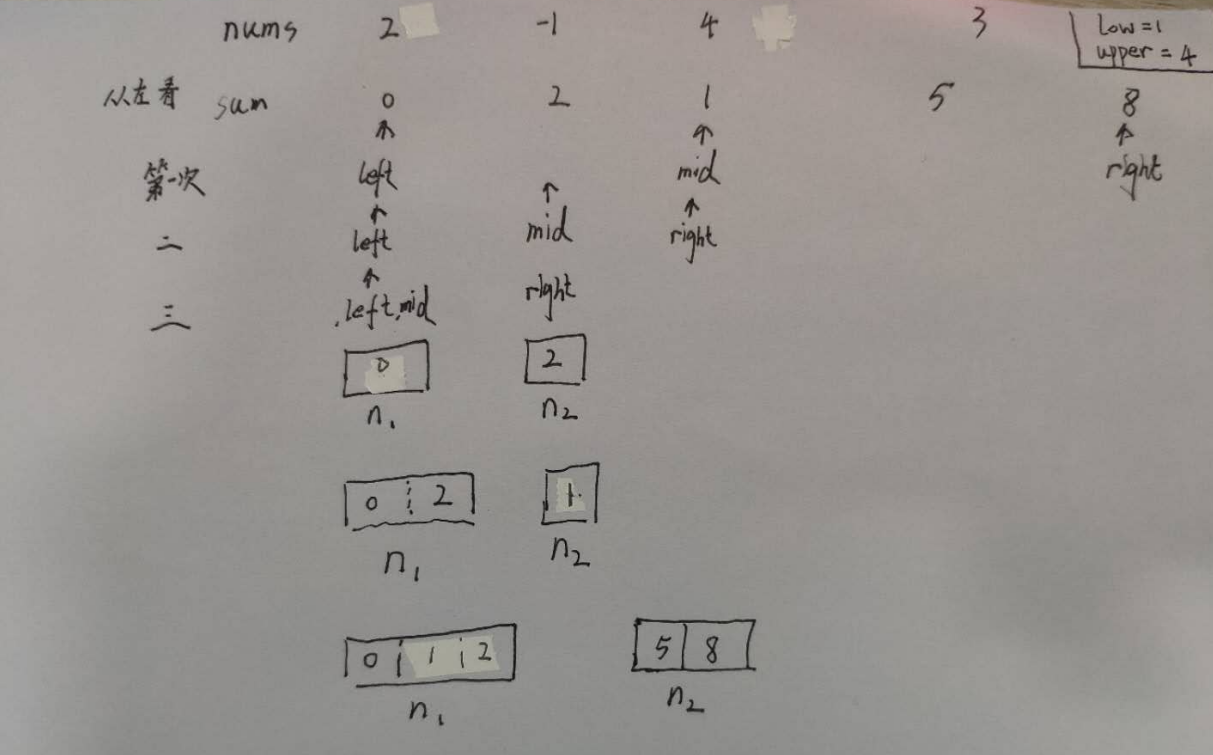
对于给定的输入:nums = [2,-1,4,3], lower = 1, upper = 4
我们可以先构造一个前缀和数组sums=[0,2,1,5,8],sums[i]就是nums数组索引[0,i-1]的和,如sums[1]=2=nums[0],sums[2]=1=nums[0]+nums[1]
那么如果想找nums的区间和,我们可以通过前缀和数组计算得出。如S(1,2)=4=sums[3]-sums[1] 找出满足要求的区间和 即可转换为 通过前缀和数组的计算获取
对于前缀和数组 我们就可以结合官方给出的导入例子来理解
可以将前缀和数组一分为二,一分为二.....。分到最小的时候(就每个组只有一个元素 从左来看即 左组为[0],右组为[2]。从右看,左组[4],右组为[3] )
我们从左来理解,两组只有一个元素,显然两组因为只有一个元素,所以两组都是升序数组。
那么我们可以使用导例,将[0]看成n1,[2]看成n2。那么则可统计符合要求下标对数量
然后我们把n1,n2进行合并,排序。 右组也是一样n1,n2合并排序,到最后从左右合并排序完,就得到了n1 = [0,1,2] n2=[5,8] 又可以求横跨两组符合要求的下标对数量
就求出了所有符合要求下标对数量
代码
class Solution {
public int countRangeSum(int[] nums, int lower, int upper) {
long s = 0;
long[] sum = new long[nums.length + 1];
for (int i = 0; i < nums.length; ++i) {
s += nums[i];
sum[i + 1] = s;
}
return countRangeSumRecursive(sum, lower, upper, 0, sum.length - 1);
}
public int countRangeSumRecursive(long[] sum, int lower, int upper, int left, int right) {
if (left == right) {
return 0;
} else {
int mid = (left + right) / 2;
int n1 = countRangeSumRecursive(sum, lower, upper, left, mid);
int n2 = countRangeSumRecursive(sum, lower, upper, mid + 1, right);
int ret = n1 + n2;
// 首先统计下标对的数量
int i = left;
int l = mid + 1;
int r = mid + 1;
while (i <= mid) {
while (l <= right && sum[l] - sum[i] < lower) {
l++;
}
while (r <= right && sum[r] - sum[i] <= upper) {
r++;
}
ret += r - l;
i++;
}
// 随后合并两个排序数组
int[] sorted = new int[right - left + 1];
int p1 = left, p2 = mid + 1; //p1用作n1 p2用于n2
int p = 0; //用作sorted右索引定位
while (p1 <= mid || p2 <= right) {
if (p1 > mid) {
sorted[p++] = (int) sum[p2++];
} else if (p2 > right) {
sorted[p++] = (int) sum[p1++];
} else {
if (sum[p1] < sum[p2]) {
sorted[p++] = (int) sum[p1++];
} else {
sorted[p++] = (int) sum[p2++];
}
}
}
for (int j = 0; j < sorted.length; j++) {
sum[left + j] = sorted[j];
}
return ret;
}
}
}