NOIP 普及组2003 题解及经验总结
1. 麦森数
题目:
形如2P−12P−1的素数称为麦森数,这时P一定也是个素数。
但反过来不一定,即如果P是个素数,2P−12P−1不一定也是素数。
到1998年底,人们已找到了37个麦森数。
最大的一个是P=3021377,它有909526位。
麦森数有许多重要应用,它与完全数密切相关。
任务:从文件中输入P,计算2P−12P−1的位数和最后500位数字(用十进制高精度数表示)。
输入格式
文件中只包含一个整数P。
输出格式
第一行:十进制高精度数2P−12P−1的位数。
第2-11行:十进制高精度数2P−12P−1的最后500位数字。(每行输出50位,共输出10行,不足500位时高位补0)
不必验证2P−12P−1与P是否为素数。
数据范围
1000<P<3100000
输入样例:
1279
输出样例:
386
00000000000000000000000000000000000000000000000000
00000000000000000000000000000000000000000000000000
00000000000000104079321946643990819252403273640855
38615262247266704805319112350403608059673360298012
23944173232418484242161395428100779138356624832346
49081399066056773207629241295093892203457731833496
61583550472959420547689811211693677147548478866962
50138443826029173234888531116082853841658502825560
46662248318909188018470682222031405210266984354887
32958028878050869736186900714720710555703168729087
代码
#include<bits/stdc++.h>
using namespace std;
const int N=500;
int p,a[N],tmp[N],res[N];
void mult(int c[],int a[],int b[])
{
memset(tmp,0,sizeof tmp);
for(int i=0;i<N;++i)
for(int j=0;i+j<N;++j)
tmp[i+j]+=a[i]*b[j];
for(int i=0,t=0;i<N;++i)
{
t+=tmp[i];
c[i]=t%10;
t/=10;
}
return;
}
void qmi(int k)
{
res[0]=1;
a[0]=2;
while(k)
{
if(k&1) mult(res,res,a);
mult(a,a,a);
k>>=1;
}
res[0]--;
return;
}
int main()
{
cin>>p;
cout<<(int)(p*log10(2))+1<<endl;
qmi(p);
for(int i=0,k=N-1;i<10;++i)
{
for(int j=0;j<50;++j,--k)
cout<<res[k];
cout<<endl;
}
return 0;
}
方法总结
1.关于求出一个高位数的位数问题:
因为 假设有一个k位数x 10(k-1)<=x<10k
所以 k-1<=lg(x);
得出 k<=lg(x)+1;
即为 k=floor(lg(x))+1;
转回到改题目:
2^p-1共有 k=floor(lg(2^p-1))+1 位数
因为2^p一定不是一个整百的数
所以2^p-1不会影响位数
所以原式可以简化位 k=floor(lg(2^p))+1;
即为k=floor(p*lg(2))+1;
2.高精度运算:
void mult(int c[],int a[],int b[])
{
memset(tmp,0,sizeof tmp);//初始化一个暂存数组
for(int i=0;i<N;++i)
for(int j=0;i+j<N;++j)
tmp[i+j]+=a[i]*b[j];//高精度乘法
//t代表进位 可以压行到for循环内
for(int i=0,t=0;i<N;++i)
{
t+=tmp[i];
c[i]=t%10;
t/=10;
}
return;
}
3.快速幂:
void qmi(int k)
{
res[0]=1;
a[0]=2;
while(k)
{
if(k&1) mult(res,res,a);
mult(a,a,a);
k>>=1;
}
//将k分成奇数部分和偶数部分 奇数部分单独运算 偶数部分减半运算
return;
}
另外:
快速幂不一定是最简便的办法:普通的乘方运算的复杂度:L*p;
快速幂的运算复杂度:L^2*log (p);
所以当且仅当 :L*log(p)<=p 的时候 使用快速幂最合适
2.栈
栈是计算机中经典的数据结构,简单的说,栈就是限制在一端进行插入删除操作的线性表。
栈有两种最重要的操作,即pop(从栈顶弹出一个元素)和push(将一个元素进栈)。
栈的重要性不言自明,任何一门数据结构的课程都会介绍栈。
宁宁同学在复习栈的基本概念时,想到了一个书上没有讲过的问题,而他自己无法给出答案,所以需要你的帮忙。
宁宁考虑的是这样一个问题:一个操作数序列,从1,2,一直到n,栈A的深度大于n。
现在可以进行两种操作,
1、将一个数,从操作数序列的头端移到栈的头端(对应数据结构栈的push操作)。
2、将一个数,从栈的头端移到输出序列的尾端(对应数据结构栈的pop操作)。
使用这两种操作,由一个操作数序列就可以得到一系列的输出序列。
你的程序将对给定的n,计算并输出由操作数序列1,2,…,n经过操作可能得到的输出序列的总数。
输入格式
输入文件只含一个整数 n。
输出格式
输出文件只有一行,即可能输出序列的总数目。
数据范围
1≤n≤18
输入样例:
3
输出样例:
5
代码
#include<bits/stdc++.h>
using namespace std;
const int N=40;
long long c[N][N];//要算到40!!!
int main()
{
int n;
cin>>n;
for(int i=0;i<=2*n;++i)
for(int j=0;j<=i;++j)//最多只能在i个数里面取出i个数 故i<=j
if(!j) c[i][j]=1;
else c[i][j]=c[i-1][j]+c[i-1][j-1];
cout<<c[2*n][n]/(n+1)<<endl;
return 0;
}
方法总结:
1.注意题目中的数据范围和所需数据范围是否相同
2.排列组合中:注意选择的个数 <= 总共的个数
3.卡特兰数总结:
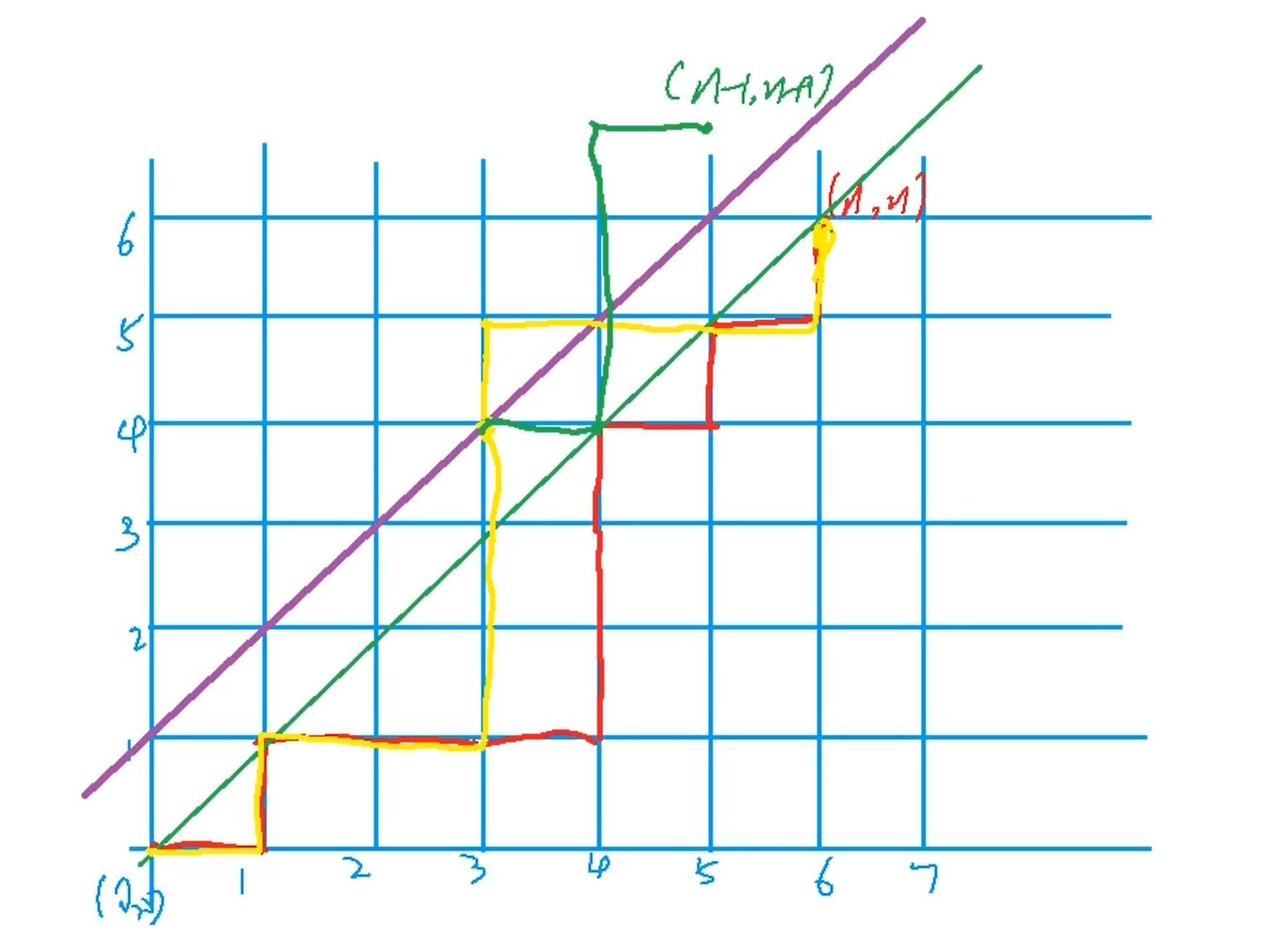
卡特兰数的证明: 一切的方案都可以转化为 在绿线以下的方案 和 触碰紫线的方案
所有触碰或超过紫线的部分,沿着紫线进行对称,会得到一个到达(n-1,n+1)的点的路径
绿线以下的部分:C(2n,n) 即在2n步中有n步是向上或向右走的
触碰或超过紫线的部分:C(2n,n-1)或C(2,n+1) 即在2n步中有n-1步是向右的或者n+1步是向上走的
最终要求的绿线以下的方案数即为:C(2n,n)-C(2n,n-1)
化简可得:C(2n,n)/(n+1)
卡特兰数使用到的关于排列组合的递推:
C(n,m)=C(n-1,m)+C(n-1,m-1);
3.数字游戏
丁丁最近沉迷于一个数字游戏之中。
这个游戏看似简单,但丁丁在研究了许多天之后却发觉原来在简单的规则下想要赢得这个游戏并不那么容易。
游戏是这样的,在你面前有一圈整数(一共n个),你要按顺序将其分为m个部分,各部分内的数字相加,相加所得的m个结果对10取模后再相乘,最终得到一个数k。
游戏的要求是使你所得的k最大或者最小。
例如,对于下面这圈数字(n=4,m=2):
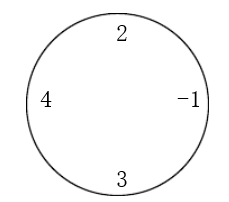
当要求最小值时,((2-1) mod 10)×((4+3) mod 10)=1×7=7,要求最大值时,为((2+4+3) mod 10)×(-1 mod 10)=9×9=81。
特别值得注意的是,无论是负数还是正数,对10取模的结果均为非负值。
丁丁请你编写程序帮他赢得这个游戏。
输入格式
输入文件第一行有两个整数,n和m。
以下n行每行一个整数,其绝对值不大于10000,按顺序给出圈中的数字,首尾相接。
输出格式
输出文件有两行,各包含一个非负整数。
第一行是你程序得到的最小值,第二行是最大值。
数据范围
1≤n≤50
1≤m≤9
输入样例:
4 2
4
3
-1
2
输出样例:
7
81
代码
#include<bits/stdc++.h>
using namespace std;
const int N=110;
const int M=15;
const int INF=0x3f3f3f;
int f[N][N][M],g[N][N][M],w[N],n,m,sum[N];
int get_mod(int x)
{
return (x%10+10)%10;
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;++i)
{
cin>>w[i];
w[i+n]=w[i];
}
for(int i=1;i<=2*n;++i)//长度为2*n
sum[i]=sum[i-1]+w[i];
//g为最大值 f为最小值
memset(f,0x3f,sizeof f);
memset(g,-0x3f,sizeof g);
for(int len=1;len<=n;++len)
for(int l=1;l+len-1<2*n;++l)
{
int r=l+len-1;
f[l][r][1]=get_mod(sum[r]-sum[l-1]);//不要放在后一个区间里
g[l][r][1]=get_mod(sum[r]-sum[l-1]);
for(int k=2;k<=m;++k)
{
if(2*n-r<m-k) continue;
for(int j=l+k-2;j<r;++j)
{
f[l][r][k]=min(f[l][r][k],f[l][j][k-1]*get_mod(sum[r]-sum[j]));
g[l][r][k]=max(g[l][r][k],g[l][j][k-1]*get_mod(sum[r]-sum[j]));
}
}
}
int maxn=-INF;
int minn=INF;
for(int i=1;i<=n;++i)
{
maxn=max(g[i][i+n-1][m],maxn);
minn=min(f[i][i+n-1][m],minn);
}
cout<<minn<<endl;
cout<<maxn<<endl;
}
方法总结
1.破环成链:
将一个环破成一条链,后将这条链复制在后面。
分别枚举起点的方案数,求出最佳的方案。
往往配合前缀和一同使用。
2.负数取模的问题:
int get_mod(int x)
{
return (x%10+10)%10;
}
第一个模10:把绝对值缩小到10以内
第二个加10:把负数的值加成正的
第三个模10:如果x本来就是正数的话,加上10之后会超过10,因此需要模10
此题因为是要先求和再求模,所以应该是get_mod(s[i]-s[j-1]);
3.动态规划的分析:
因为是递推,所以先枚举长度,再枚举左端点,后可以用左端点和长度之间的关系表示出右端点。
如果分成k份(k<=m) 应该枚举一个分组的指针j:
因为最小的右端点符合式子:L+x-1; 最小左端点符合式子:L+x
(注意一个点并不是两个区间都可以包含)
代入x=k-1得 最小右端点的式子为L+k-2,最小左端点的式子为L+k-1;
4.注意关于求最大最小值时候的初始化
5.最后取最大最小值的时候一定要遍历所有的起点
乒乓球
国际乒联现在主席沙拉拉自从上任以来就立志于推行一系列改革,以推动乒乓球运动在全球的普及。
其中11分制改革引起了很大的争议,有一部分球员因为无法适应新规则只能选择退役。
华华就是其中一位,他退役之后走上了乒乓球研究工作,意图弄明白11分制和21分制对选手的不同影响。
在开展他的研究之前,他首先需要对他多年比赛的统计数据进行一些分析,所以需要你的帮忙。
华华通过以下方式进行分析,首先将比赛每个球的胜负列成一张表,然后分别计算在11分制和21分制下,双方的比赛结果(截至记录末尾)。
比如现在有这么一份记录,(其中W表示华华获得一分,L表示华华对手获得一分):
WWWWWWWWWWWWWWWWWWWWWWLW
在11分制下,此时比赛的结果是华华第一局11比0获胜,第二局11比0获胜,正在进行第三局,当前比分1比1。
而在21分制下,此时比赛结果是华华第一局21比0获胜,正在进行第二局,比分2比1。
如果一局比赛刚开始,则此时比分为0比0。
你的程序就是要对于一系列比赛信息的输入(WL形式),输出正确的结果。
输入格式
每个输入文件包含若干行字符串(每行至多20个字母),字符串由大写的W、L和E组成。
其中E表示比赛信息结束,程序应该忽略E之后的所有内容。
输出格式
输出由两部分组成,每部分有若干行,每一行对应一局比赛的比分(按比赛信息输入顺序)。
其中第一部分是11分制下的结果,第二部分是21分制下的结果,两部分之间由一个空行分隔。
输入样例:
WWWWWWWWWWWWWWWWWWWW
WWLWE
输出样例:
11:0
11:0
1:1
21:0
2:1
代码
#include<bits/stdc++.h>
using namespace std;
void work(string str,int score)
{
int a=0,b=0;
for(int i=0;i<str.length();++i)
{
if(str[i]=='W') a++;
else b++;
if(max(a,b)>=score&&abs(a-b)>=2)
{
cout<<a<<":"<<b<<endl;
a=b=0;
}
}
cout<<a<<":"<<b<<endl;
}
int main()
{
string str;
char c;
while(cin>>c,c!='E') str+=c;
work(str,11);
puts("");
work(str,21);
return 0;
}
方法积累
1.注意关于比赛赛制:
特殊地:分制比赛中,两个人分数的绝对值不能小于2;
既然绝对值不能小于2,就一定存在大于原有分制的分的可能性,因此要时刻去判断是否两者分数的最大值大于了规定的分数,因此两个条件之间的关系为并列。