首先说一下,对一个刚学Trie树的蒟蒻来说(就是我),这道题是一道好题。Trie树比较简单,所以就不详细写了。
Rima
内存限制:256 MiB
时间限制:1000 ms
标准输入输出
题目类型:传统
评测方式:文本比较
上传者: cqbzgm
题目描述
Adrian对单词押韵很感兴趣。如果两个单词的最长公共后缀的长度与两个单词中较长那个的长度一样,或者等于较长单词的长度减一,则这两个单词押韵。换句话说,如果A,B的最长公共后缀LCS(A,B)≥max(|A|,|B|)-1,则A和B押韵。有一天,在阅读一套短篇小说时,他决定创造出能够使每两个相邻单词押韵的最长的单词序列,序列中的每个单词只能出现一次。但是Adrian已经厌倦了这个任务,所以他决定回去读小说,并要求你代替他解决这个任务。
输入格式
第一行输入包含整数N(1≤N≤5*1e5)。表示单词的个数。接下来N行每行包含一个只由小写英文字母组成的字符串。表示可以用于组成序列的单词。数据保证每个单词都是不同的,保证所有单词的长度之和不超过3*1e6。
输出格式
输出一个整数。表示单词序列的最长长度。样例
样例输入1
4
honi
toni
oni
ovi
样例输出1
3
样例输入2
5
ask
psk
krafna
sk
k
样例输出2
4
样例输入3
5
pas
kompas
stas
s
nemarime
样例输出3
1
数据范围与提示
对于30%的数据,N≤18。
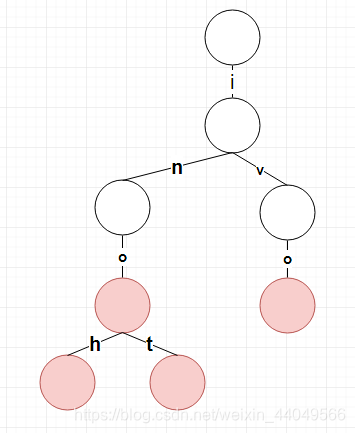
首先这道题要用到的是最长公共后缀,所以可以倒着将字符串插入字典树中以方便操作。那么我们便将样例1插入字典树中:
我们可以发现,在Tri树中,具有“押韵”关系的两个点,它们的"end"节点必定是父子或者是兄弟关系,没有例外。(比如oni和honi的end节点就是父子关系,honi和toni就是兄弟关系。)
答案已经很明显了。现在要考虑的是方法。
在考场中,我用的方法是从树的叶节点开始搜索,统计出连通的end节点的数量(这里连通的定义是具有父子关系或兄弟关系)。这样做没有问题,也很好想,但它是错的。如果我们直接暴力统计的,我们会忽略一些特殊情况(虽然这样可以骗至少40分)
这组数据:
7
ab
aab
ccb
cb
bbb
bb
b
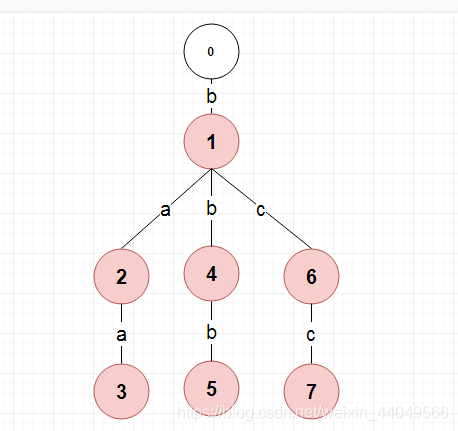
如果使用刚才我说的直接统计每个节点在它的子树中end节点的数量(这个节点不一定是end节点,因为这样还包括两个end节点是兄弟的情况),那么它就会输出7,而正确答案却是6。
造成答案错误的原因是我们忽略了题目中的一个限制条件。在这个队列中,只有“相邻”的两个单词押韵才符合答案。
在1节点中,我们直接统计了红点的个数7个。但我们无论如何都无法将"ab","aab","ccb","cb","bbb","bb","b"这7个单词排在一起。原因是因为“b”旁边只能排有2个单词
我们可以按"aab" "ab" "b" "bb" "bbb"的顺序排列我们可以在"ab"和"b"之间插入一个"cb",这样就变成了"aab" "ab" "cb" "b" "bb" "bbb"。但"ccb"却怎么也插不进去了。
让我们回到Tri树中。使用(f_{u})数组来表示一个单词它后面(注意是后面,这意味着这个单词只能接一边。而不能将其它单词接到它的前面。)的最多能接上单词的数量。
关于它的状态转移方程 :
(f_{u}=max(f_{v}) +sum) ((sum)表示u的子节点中除了f值最大的一个v节点外其它合法子节点的数量(合法意味着这个节点是end节点))
但f数组却不是最终的答案。注意我们对它的定义是在它的后面,也就是只能接上一边,所以状态转移方程不是(f_{u}=max1(f_{v1}) +max2(f_{v2})+sum)
((max1) 和(max2)是第一大和第二大)
在每个节点中,定义(ans=max1(f_{v1}) +max2(f_{v2})+sum),答案就是最大的(ans).
(你们直接看代码吧,我自己也解释不清)
#include <iostream>
#include <string>
#include <cstdio>
#include <map>
#include <cstring>
using namespace std;
#define N 500010
#define M 3000010
#define LL long long
string A;
int n,p[M][30],k=1,ans,f[M];
bool IsEnd[M];
void Insert(string A) {
int now=1;
for(int i=A.length()-1;i>=0;i--) {
if(!p[now][A[i]-'a'])
p[now][A[i]-'a']=++k;
now=p[now][A[i]-'a'];
}
IsEnd[now]=1;
}
void dfs(int x) {
int sum=0;
pair<int,int> maxx;
maxx=make_pair(0,0);
for(int i=0,v;i<26;i++)
if(p[x][i]) {
v=p[x][i];
if(IsEnd[v]) sum++;
dfs(v);
maxx=max(maxx,make_pair(maxx.first,f[v]));//这里不用pair也行,但我用其他方法
maxx=max(maxx,make_pair(f[v],maxx.first));//就WA了,所以吹爆pair
f[x]=max(f[x],f[v]);
}
if(IsEnd[x]) f[x]+=max(1,sum);
else f[x]=0;
ans=max(ans,IsEnd[x]+maxx.first+maxx.second+max(0,sum-2));
}
int main() {
cin>>n;
for(int i=1;i<=n;i++) {
cin>>A;
Insert(A);
}
dfs(1);
cout<<ans;
}