简介:
莫队这个算法是莫涛提出的。 用于处理一类不带修改的区间查询问题的离线 算法,其核心在于利用曼哈顿距离最小生成树 算法对区间处理顺序进行处理 。
——zrt课件
这个算法本质上其实是暴力,但是由于可以离线处理循环的顺序,使得复杂度可以从n^2降到n^根号n甚至更低。
对于可以找到以下特点的题可以尝试使用莫队:
1.莫队算法是离线处理一类区间不修改查询类问 题的算法。就是如果你知道了 [ L,R] 的答案。你 可以在 O(1 ) 或 O( lgn ) 的 时间下得到 [ L,R
1] 和 [ L,R+1] 和 [ L1,R] 和 [ L+1,R] 的答案的话。就可 以使用莫队算法 。
2.需要预知所有的询问
例题一:
小Z把这N只袜子从1到N编号,然后从编号L到R(L 尽管小Z并不在意两只袜子是不是完整的一双,甚至不在意两只袜子是否一左一右,他却很在意袜子的颜色,毕竟穿两只不同色的袜子会很尴尬。
你的任务便是告诉小Z,他有多大的概率抽到两只颜色相同的袜子。当然,小Z希望这个概率尽量高,所以他可能会询问多个(L,R)以方便自己选择。
分析:
通过组合数学推理可以得知:
对于 L,R 的询问。设其中颜色为 x,y,z ... 的 袜子 的个数为 a,b,c ...
那么答案即为 (a*(a-1)/2+b*(b-1)/2+c*(c-1)/2....)/((R-L+1)*(R-L)/2 )
化简得 :(a^2+b^2+c^2+...x^2-( a+b+c+d +.....))/((R-L+1)*(R-L ))
即: (a^2+b^2+c^2+...x^2-(R-L+1))/((R-L+1)*(R-L))
所以我们需要维护的是,从L到R这个区间中的每个袜子的种类数的平方和。
我们在移动L、R的时候,增加一个,sum+=cnt[x]×2.减少一个,sum=sum-cnt[x]×2+2 (sum是分子的总值。)
发现我们需要不断移动L、R,所以我们必须将所有的询问进行恰当的排序,使得L、R的移动次数尽可能小,才能降低时间复杂度。
首先要分块处理。
必须分块,如果单纯的通过l相等,按r排序的方法,可能会在l移动一个单位,r就要从另一边返回来,实际很慢。
之后我们这样排序:
struct node{ int l,r; int hao; bool friend operator <(node a,node b) { if(id[a.l]==id[b.l]) { if(id[a.l]&&1==1) return a.r<b.r; else return a.r>b.r; } return id[a.l]<id[b.l]; } }q[N];
先按照左端点所在块排序,再按照右端点排序。要注意的是:if(id[a.l]&&1==1) return a.r<b.r; else return a.r>b.r;
左端点所在块是奇数的时候,升序排列,否则降序排列,这样可以在L增加到下一个块的时候,r移动次数尽量小,最好情况下每次可以省n次,l最多跳n/unit次,可以省去n×n/unit次,当然绝大多数情况远没有这么好。
本题大概可以省去一共180ms
最后直接分子分母求gcd化简即可。
注意long long
详见代码:
#include<bits/stdc++.h> #define ll long long #define num ch-'0' using namespace std; const int N=100000+10; ll kua; void read(int &x) { x=0;char ch; while(!isdigit(ch=getchar())); for(x=num;isdigit(ch=getchar());x=x*10+num); } int n,m; int id[N]; struct node{ int l,r; int hao; bool friend operator <(node a,node b) { if(id[a.l]==id[b.l]) { if(id[a.l]&&1==1) return a.r<b.r; else return a.r>b.r; } return id[a.l]<id[b.l]; } }q[N]; ll ans[N][2]; int a[N]; ll cnt[N]; ll sum; int L,R; ll gcd(ll x,ll y) { return y==0?x:gcd(y,x%y); } int main() { read(n),read(m); kua=sqrt(n); for(int i=1;i<=n;i++) read(a[i]),id[i]=(i-1)/kua+1; for(int i=1;i<=m;i++) read(q[i].l),read(q[i].r),q[i].hao=i; sort(q+1,q+m+1); for(int i=1;i<=m;i++) { //cout<<i<<" : "<<q[i].l<<" "<<q[i].r<<" "<<" from "<<q[i].hao<<endl; if(i==1){ L=q[i].l,R=q[i].r; sum=0; for(int j=q[i].l;j<=q[i].r;j++) { cnt[a[j]]++; } for(int j=1;j<=n;j++) if(cnt[j]) sum+=cnt[j]*cnt[j]; sum=sum-(ll)(q[i].r-q[i].l+1); ans[q[i].hao][0]=sum; ans[q[i].hao][1]=((ll)q[i].r-q[i].l+1)*((ll)q[i].r-q[i].l); } else{//duo 1 : sum+ 2*cnt[a[j]] //shao 1: sum- 2*cnt[a[j]]+2 if(R<q[i].r) { while(R<q[i].r) { R++; sum=sum+2*cnt[a[R]]; cnt[a[R]]++; } } else if(R>q[i].r) { while(R>q[i].r) { sum=sum-2*cnt[a[R]]+2; cnt[a[R]]--; R--; } } if(L<q[i].l) { while(L<q[i].l) { sum=sum-2*cnt[a[L]]+2; cnt[a[L]]--; L++; } } else if(L>q[i].l) { while(L>q[i].l) { L--; sum=sum+2*cnt[a[L]]; cnt[a[L]]++; } } ans[q[i].hao][0]=sum; ans[q[i].hao][1]=((ll)q[i].r-q[i].l+1)*((ll)q[i].r-q[i].l); } //cout<<" after "<<sum<<endl; } for(int i=1;i<=m;i++) { ll t1=ans[i][0],t2=ans[i][1]; if(t1==0) t2=1; else{ ll g=gcd(max(t1,t2),min(t1,t2)); t1/=g; t2/=g; } printf("%lld",t1); printf("/"); printf("%lld ",t2); } return 0; }
但是莫队还可以处理一个更高级的题目种类。
带修改的题也可以考虑做!!
这样一个struct需要维护L,R,T三个,T为该询问是在第几次操作之后询问的。可以看做是一个time
例题二:
分析详见友链(推荐):莫队算法——大米饼
排序:
struct node{ int l,r,t; int hao; bool friend operator <(node a,node b) { if(id[a.l]==id[b.l]) { if(id[a.r]==id[b.r]) { if(id[a.r]&1) return a.t<b.t; return a.t>b.t; } return a.r<b.r; } return a.l<b.l; } }q[N];
代码:
#include<cstdio> #include<cstdlib> #include<algorithm> #include<cmath> #include<iostream> #include<cstring> #define num ch-'0' using namespace std; const int N=100000+10; void read(int &x) { x=0;char ch; while(!isdigit(ch=getchar())); for(x=num;isdigit(ch=getchar());x=x*10+num); } int sum; int n,m; int a[N],b[N]; int cnt[1000000+10]; int id[N],len; int ans[N]; int tim[N][3]; struct node{ int l,r,t; int hao; bool friend operator <(node a,node b) { if(id[a.l]==id[b.l]) { if(id[a.r]==id[b.r]) { if(id[a.r]&1) return a.t<b.t; return a.t>b.t; } return a.r<b.r; } return a.l<b.l; } }q[N]; inline void add(int x) { cnt[a[x]]++; sum+=(cnt[a[x]]==1); } inline void del(int x) { cnt[a[x]]--; sum-=(cnt[a[x]]==0); } inline void add2(int ti,int l,int r,int k)//1->2 jia k { if(l<=tim[ti][0]&&tim[ti][0]<=r) { cnt[tim[ti][k]]++; sum+=(cnt[tim[ti][k]]==1); } a[tim[ti][0]]=tim[ti][k]; } inline void del2(int ti,int l,int r,int k)//2->1 shan k { if(l<=tim[ti][0]&&tim[ti][0]<=r) { cnt[tim[ti][k]]--; sum-=(cnt[tim[ti][k]]==0); } } char que; int has; int tot; int main() { read(n);read(m); len=pow(n,0.666666); for(int i=1;i<=n;i++) read(a[i]),b[i]=a[i],id[i]=(i-1)/len+1; int x,y; has=0; for(int i=1;i<=m;i++) { scanf("%c",&que); if(que=='Q') { tot++; read(x);read(y); q[tot].l=x,q[tot].r=y; q[tot].t=has; q[tot].hao=tot; } else{ has++; read(x);read(y); tim[has][0]=x;tim[has][2]=y; tim[has][1]=b[x]; b[x]=y; } } sort(q+1,q+tot+1); int L,R,T=0; for(int i=1;i<=tot;i++) { if(i==1) { L=q[i].l,R=q[i].r; for(int j=q[i].l;j<=q[i].r;j++) { cnt[a[j]]++; sum+=(cnt[a[j]]==1); } while(T<q[i].t) ++T,del2(T,L,R,1),add2(T,L,R,2); ans[q[i].hao]=sum; } else{ while(T<q[i].t) ++T,del2(T,L,R,1),add2(T,L,R,2); while(T>q[i].t) del2(T,L,R,2),add2(T,L,R,1),T--; while(L<q[i].l) del(L++); while(L>q[i].l) add(--L); while(R<q[i].r) add(++R); while(R>q[i].r) del(R--); ans[q[i].hao]=sum; } } for(int i=1;i<=tot;i++) printf("%d ",ans[i]); return 0; }
莫队算法——暴力出奇迹。
在做题实在没有思路的时候,不要忘了莫队。
upda:2019.3.24:
更新:
2.还有回滚莫队:说白了就是栈序撤销
这样方便维护最大值莫队算法——从入门到黑题 - WAMonster - 博客园

3.一般序列莫队,block=n/sqrt(m)最优
mblock+(n/block)*n最小
均值不等式
4.带修莫队最好这样排:
l,r都分块
l块相同,r块相同,t按照(l块+r块)的奇偶性升序降序排
如果r块不同,按照l块的奇偶性升序降序排
大概长这样:
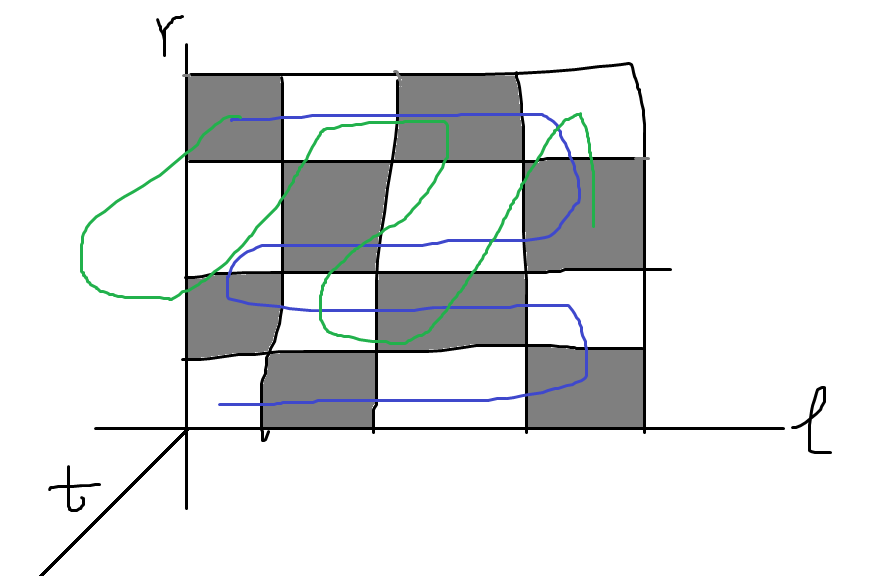
绿色的是t轴变化
这样常数最小