本文章记录所错、易错细节要点。
0.AC KILLER:(按照出错概率排序)
①爆int WA到吐血(变量int,函数返回值int,乘法爆int,取模忘了爆int)
②数组开小RE
③审题不清WA
④n,m写反,i,j写反WA,主观臆断各种写错变量名
还有不是什么都是n!!!!
2018.10.30模拟赛,d写成n,血亏100pts
⑤卡常数TLE
⑥爆栈RE/MLE
⑦没有算清内存MLE(一般要有预留几十MB)
⑧输出没有%lld 前功尽弃
0.5 思维固化错误之看错、写错变量名
做题做多了,有的时候想当然。
①n不一定是点数,m不一定是边数,q不一定是询问!!
②不是什么东西都是对n操作!!!
总之,冷静分析,一切看好题目要求!!
1.printf("%lld",ans); printf("%d",ans); long long -> %lld d -> %d (poj1456 Supermarket)( bzoj 1231 mixup)
输出一定要注意lld~!!~~~~~~~~~~~~~~~~!!!!!!!!!!!!!!!!!
2.注意数组下标开始地址。 string:0-strlen-1 (kmp manancher)
3.注意是否数组内减法(加法)会使越界(或小于0)
注意在取queue,q.pop()的时候,判断是否为空。 (poj 3784 Median)
4.注意特殊边界情况: n=1;m=0;e<0等等 (poj3013 Big Chirstmas Tree)
5.对于多种数据题型:
(1)注意清空之前的数据。 memset(bian,0,sizeof (struct node)*N) (poj系列)
memset(hd,0,sizeof hd); cnt=0;
(2)poj做题,注意是一组数据还是多组 (poj1325 Machine Schedule)
(3)多组数据中,特判加跳过时,注意输入完该组之后的数据,防止这些垃圾数据被后面一组数据吃掉,影响答案。(时间复杂度,判断是否合法)注意要保证t--(就算是特判跳过,也要带上t--)(zoj 1239Hanoi)
6.注意输出英文大小写以及标点! Yes、YES、No、NO、!、。、?、空格.etc (poj 1135Domino Effect)(时间复杂度)
7.数位DP注意前导零的处理。 在0~99999(len-1个)时产生。 (luogu 2602数字计数)
8.prim算法中,从优先队列中取出来的一条边一定要判断两端的点是否已被加入树中。 if(vis[a]&&vis[b]) bian++,continue; 典例:poj2728Desert King
9.st表中,f[i][j]表示:[i,i+2^j-1]最值。 并且,倍增时必须在外层循环j,由小块倍增到大块。 倍增:
for(int j=1;(1<<j)<=n;j++)
for(int i=1;i+(1<<j)-1<=n;i++)
{
st[i][j]=min(st[i][j-1],st[i+(1<<(j-1)][j-1];
}
查询:
scanf("%d%d",&l,&r);
int len=log2(r-l+1);
ans=min(st[l][lrn],st[r+1-(1<<len)][len])
10.输入边的循环时,注意是:for(1,m,i++) 不是for(1,n,i++) 要分清点数n和边数m。
11.邻接表建无向图:bian[2倍M] 双向。 RE无数。(luogu3629 巡逻)
12.有查询更改操作的题中,先读入“q”,分情况操作,不要一次性读完之后的具体操作。以免用字符读入两位数爆零。 (寒假%你赛,luogu1383高级打字机)
13.memset时,检查是否全部清空。 (poj3694)
14.LCA时,dep[0]=-1;
if(dep[x]<dep[y]) swap(x,y);(注意是小于) (poj3694)(poj3417)
15.有时候,一张map可能要从上到下循环一遍,再从左到右循环一遍,
即:先是for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) 再是for(int i=1;i<=m;i++) for(int j=1;j<=n;j++) 一定注意的是:如果第二次将i定为列号,j定为行号时,找地图时一定要:a[j][i] 千万不能i,j写反了!!!!(在n!=m的时候就惨爆了)(AC100变爆零)(luogu2825 游戏)(ezoj 游戏)(3.24图论考试)
16.tarjan、边双联通分量时, 第三步染联通块时: for(int i=1;i<=n;i++) if(!c[x]) { dcc++; dfs(x); } (注意大括号位置扩全)
17.树状数组: 1.注意query、add中x的加减以及上下界不要弄混。 2.推荐x+=x&(-x),而不使用lowbit,不调用函数可以加速。 (HDOJ 5542)
int query(int x)
{
int tot=0;
for(;x;x-=x&(-x))
tot+=tr[x];
return tot;
}
void add(int x,int c)
{
for(;x<=n;x+=x&(-x))
tr[x]+=c;
}
18.单调队列优化dp,注意单调队列中可以单调的部分是什么,比较时一定要比较完整。 f[q[hd]]+kq[hd]+m>f[i]+kf[i]+m 一定不能丢掉一次项,常数项等。 (luogu 瑰丽华尔兹,股票交易)
19.注意,变量设为long long 的时候,输入记得也用%lld。(实在忘了long long就#define int long long)(poj2482 Stars in your window)
20.有许多棵树的时候,千万不要忘了根节点编号。其中线段树一般根节点都是1,不要和其他树混淆。 (树链剖分6h鏖战)
21.取模减法的时候,出现了负数,取模后还会是负数,所以要(x+p)%p;保证正数
(P3197越狱)
22.线段树常规操作,不要忘了mod,不要忘了add时候,sum+=add×(r-l+1)
23.对于一些数据,可能根据这个原来顺序先进行了一次记录,用p[i]表示数组第i个数的某些信息。但是之后,这个数组又用其他的排序方式进行了排序,导致p[i]已经与原来的数组不对应了。导致WA掉。这也体现了结构体的优势。(USACO2009 安全出行)
24.压位高精处理字符串读入的时候,非常恶心。
先确定是几个cur,再从后往前每logmod个转化为long long,其中每个logmod内部的顺序都是从左往右,最后的cur不够就算了。最后的cur一定是最高位注意。

void insert(char *p){
int l=strlen(p);
init();
cur=(l-1)/9;
int mm=l%9;
if(mm==0) mm=9;
for(int j=0;j<cur;j++)
for(int i=mm+(cur-1-j)*9;i<=mm+(cur-1-j)*9+8;i++)
{
s[j]=s[j]*10+p[i]-'0';
}
for(int i=0;i<mm;i++)
s[cur]=s[cur]*10+p[i]-'0';
}
不能想清楚的话,就手玩考虑直接输出是不是原始串就好了。
25.考试的时候,文件读入:
freopen("blabla.in","r",stdin);
freopen("blabla.out","w",stdout);
fclose(stdin)
fclose(stdout)
记不住会爆零的。
26.BSGS大步小步走,
分块算法的时候,块数up=floor(1.0*(sqrt(fai(P)))+1,每块内也是up个元素,注意最后一定要加一。否则下取整会导致最右边界不到fai(P)
EXBSGS扩展大步小步走,
gcd已经除完了后,NB由B*(A/πg)^(-1)得到,记得mod C。C不断在变化,每次都要mod C。日常模一模。
27.矩阵乘法:注意没有交换律,重载的运算符:
tr operator *(const tr &b)表示:c=a*b,其中b是乘矩阵,不要写反。想象一下乘的顺序,与一般乘法分开。(沼泽鳄鱼)
28.EXGCD:ax+by=gcd(a,b)
记得解得的x,y可能是负值,需要正值的时候,x=(x%(b/gcd)+(b/gcd))%(b/gcd) 注意是%(b/gcd)这样才是通解。(BSGS,EXBSGS等求逆元)
29.亲测:高斯消元的时候,eps设得小,比什么都有用。eps至少也得是1e-8不行开long double 到1e-10
不过,题目保证有解的时候,其实不需要eps,需要判是否为0的时候才需要f(abs)<eps,因为有-0.000000
(HNOI游走 卡精度神题)
判断 绝对值最大的、比较是否交换的时候,不用eps,而必须判是否为0的时候,必须有eps
尤其是是否为0会影响决策时:
(JLOI装备购买 判断是否不为0 从而决策)
30.floyd矩阵算经过k条边的最短路的时候,注意矩阵的建造(注意理解构造的含义,A^k为经过k条边的最短路)。
a[i][j]=min(b[i][k]+c[k][j)
①可以理解为的单位矩阵,A^0,相当于经过0条边的最短路,就是(i,i)等于0的矩阵,其他都是inf
②初始的矩阵(并非是单位矩阵)就是经过一条边的最短路,(i,i)都是inf(无自环时),别的有联通就是边权(重边取min),否则inf
注意对矩阵的理解。全inf并非单位矩阵,而是清空成inf矩阵。
总之,从i~k,k~j的最短路做和取min来理解就好了。
或者考虑我们普通n^3floyd怎么做的。都是先把(i,i)=0,其他inf
31.当数组中可能遇见负数的时候,可以考虑采用修正值fix,将取值的区域平移。
如:NOIP2016 D1T2 天天爱跑步, 处理d[si]-2*d[lca]<0 , w[x]-d[x]<0时,取值范围在:[-n,n]
直接再加上n,平移到[0,n]就可以直接处理了。
32.多组数据的时候,一定要注意数据的清空clear()函数要写全。
对了,一定要在主函数里启用该函数。(luogu3385 负环)
33.差分约束中,可能会有很多的类似:s[i]-s[i-1]>=0 , s[i-1]-s[i]>=-1 等等
这些边是固定的,可以不用在邻接表中存储。spfa找出来的时候,直接找边就好了。
剩余的边再用邻接表,空间均摊O(常数)/个,或者vector。
这样就防止在空间紧张的时候MLE,(POJ1201 Intervals)
34.bitset左移右移的时候,和二进制数是一样的。右移变小,左移变大。(和平时的数组从左到右不一样)
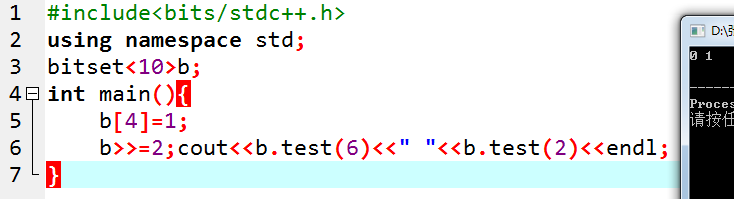
一定注意!
35.bitset 用[] 数组越界会被坑死。和一般的数组不一样,bitset用[]本地不会编译出RE,交上就挂了。
而且,bitset数组越界忍耐度非常非常的强。。。
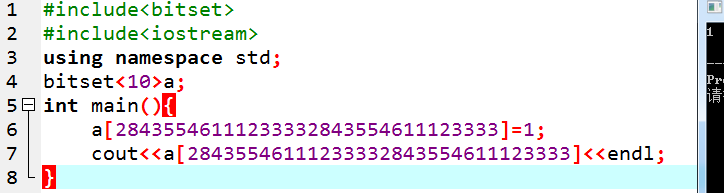
甚至:
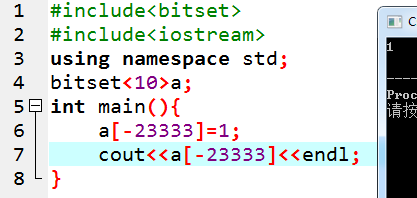
但是用set、test就很敏感了。可以精确地指出数组越界:
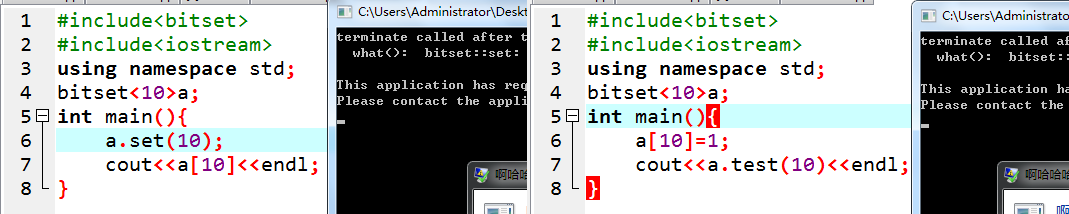
(就是打起来麻烦)
36.位运算优先级
注意状压的时候,if((s&(1<<i))==0) 注意,==的优先级更高,记得加括号。!!!
另外,线性基最后求最大值的时候,if((ret^a[i])>ret) ret^=a[i] 也要加括号!!
37.对于多组数据要清空的时候,注意是否清空干净!!
错误:其中cnt是抛物线的计数数组
struct node{
double a,b;
int kill;//binary number
}lin[N*N+N];
int cnt;
只在clear中清除了cnt
但是,再次使用kill的时候,直接按位或了,导致之前的信息还存在。
a,b两个参数没有问题,因为是直接赋值。但是对于ans,sum,tot之类要累加的,或者像这个要 按位操作的(也是一种累加)
必须要注意清零!!(NOIP2016 愤怒的小鸟 AC100->15)
38.对拍的时候,
rand函数部分:
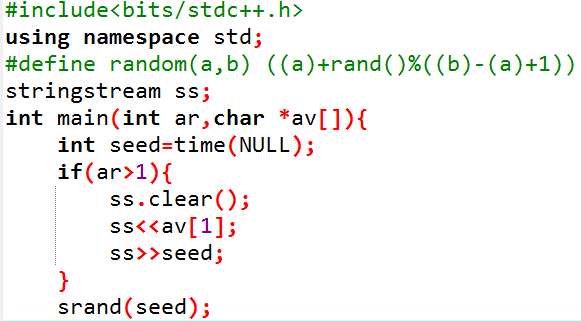
注意: *av[] 和 av[1]
还有对拍部分:
@echo off
:loop
rand.exe %random% > data.in
std.exe < data.in > std.out
my.exe < data.in > my.out
fc my.out std.out
if not errorlevel 1 goto loop
pause
goto loop
注意: “:loop” “@echo off” " % random % >" " not error level 1 "
39.没有负边权,少用spfa
亲测:[JLOI2011]飞行路线:
spfa:bzoj 7944ms ; 洛谷 不开O2 TLE 3个点 ; 开O2 TLE 1 个点
dij:bzoj 460ms ;洛谷 不开 O2 总共980ms Ac
spfa想卡还是可以卡的。不要管啥O(KE) E<50000想卡也能卡。。。。
在没有负边权,mlogm铁定能过的情况下,dij要稳定的多...
40.注意输入输出%lld!!!
必须用%lld,否则会把变量变成int
41.注意,指数在取模运算中不能直接对p取模!!因为不等价。
但是,可以对phi(p)取模,前提是“底数和p互质”
因为,a^(phi(p)) = 1 mod p 当 (a,p)=1;
对于指数取模的时候,可能会当指数是一个组合数,要预处理或者现算的时候,就必须mod phi(p)了
p是质数的时候,phi(p)=p-1
42.线性递推逆元:inv[i]=(p-[p/i])*inv[p%i] mod p
证明:[p/i]*i+p%i = 0 mod p
p%i = -[p/i]*i mod p 两边同时除以(p%i * i)
inv[i] = -[p/i]*inv[p%i] mod p
inv[i] = (p-[p/i])*inv[p%i] mod p
43.记得开long long (不知道说了多少遍了)
10^5*10^5稳爆int啊!!(RYOI9.4 T1 15pts是我的噩梦)
3*10^5 * 3* 10^5 稳爆int啊!!!(NOIP2017列队 爆int)
44.注意dfs1不要写到dfs2里去!!!
45.注意,1000000结构体排序会卡常,set更卡常!!(RYOI9.4 T2 15pts是我的噩梦)
46.注意,rotate写法:
void rotate(int x){
int y=t[x].fa,d=t[y].ch[1]==x;//初始
t[t[y].ch[d]=t[x].ch[d^1]].fa=y;//换儿子
t[t[x].fa=t[y].fa].ch[t[t[y].fa].ch[1]==y]=x;//换父亲
t[t[x].ch[d^1]=y].fa=x;//互相换
pushup(y);//更新
//pushup(x);
}
47.注意审题,仔细多确认几遍,不要立刻开始做!!
细致=审题细致+码题细致
48.prim注意vis[j]加入了点集就不要找了。
49.dist两点距离:(x1,y1,x2,y2)比较好,第一个点,第二个点顺序不会错。
50.字符询问输入
注意,字符输入不要什么ch=getchar()两次,换行符可能很多,还可能有空格。。。。。数据不靠谱。
直接ch[2] scanf(“%s”,ch) 然后if ch[0]==Q多好。直接过滤空格换行符。
51.点分治:
时刻注意if(vis[e[i].to]) continue
注意根的统计处理。
最初的size之后就不能用了,还要从重心G重新dfs
必要时可以容斥。(
)
52.平衡树删点的时候,注意判断是否是multi的,即是否可以重复以致于不用删完。
加点的时候,每次路径上的点,sz都要++,注意,相同权值的点,是不是能重复存在。
注意,每次splay前,必须保证x已经pushdown,处理区间完毕后,pushup(r),pushup(l)
(维修序列7h)
解决方法:splay前,一般都有一个rnk或者kth查找这个点,期间pushdown
pushup别忘了,在splay和区间处理完的两个特殊点。
53.特别注意:
在递归、分治、换根的函数中,全局变量的数组/vector是共用的!!!
这意味着,如果上一层还要用到这个vector(没用完)那么子区间是不能用这个vector的!!否则就全乱了。
(K大数查询,分治下去的询问vector不能共用)
解决方法:vector开一个内存回收池。一次性开够2*logn一般就2*64或者2*32个,每次回收,然后取出用完的。
(概率充电器,前缀儿子的连乘积每用完,儿子节点不能重新用!)
解决方法:由于所有的儿子节点个数总和是O(n)的,可以考虑开节点个数个vector
在每一层开一个vector也可以。
(树形背包:虽然没有例题,前几个儿子的组合g[i])
背包一般范围就比较小了,可以直接每层开一个数组。弹栈也不会很慢。
54.如果需要拆点的话,点的个数不要弄错。
网络流中,通常把一个点拆成入点和出点,两倍
边数也要注意。日常RE
55.换根的时候建议新开一个g[i]表示以i为根的答案。传入一个fa就好。
比较方便。传入答案还可能把参量不小心设成int,导致long long 爆炸
sol(int x,int dis)([Usaco2018 Feb]Directory Traversal)
56.(ans+=now)%=mod
%=mod,'='不要丢~!
57.树状数组的区间加就是一个差分,如果开始都是修改,最后统一查询1~n的话,直接用数组就好了。
最后一个前缀和累加上来就可以了。
不用树状数组logn复杂度!
(借教室,CF17E Palisection)
58.贪心微扰法排序的时候,会重载小于号。
注意,这个小于关系是否满足传递性?即是否有:$a<b,b<c o a<c$
注意,重载的小于号不能带=,否则,快排由于有一句:
$while(a[i]<a[x])space i++$
如果x是最后一个,而<变成<=,那么,i到x位置不会停止,往后走就越界了。
(luoguP2123 皇后游戏)
59.真·AC100变爆零
T2忘了输出剩余字符串长度!!!!!!!!
T1忘了还有365组数据,直接TLE!!
详见:9.26模拟赛
60.tarjan的时候,缩完的点有重边。
如果要用到缩完点的图转移的话,一定要注意!!!
如果只是取 max,可以vis标记点的访问。
如果是一个计数dp,那就要注意了。可以尝试sort或者map加新边的时候去个重。
(解决方案:每次tarjan加边的时候考虑一下是否会影响。)
61.RE?数组开小了?
(解决方案:做完这个题的时候,习惯性地再检查一遍是否有数组越界情况。
有的时候,权值下标比较注意,编号下标却经常越界~~~~)
62.不能在mo意义下求max!
显然,模意义下大,并不代表实际下大。
AC100变40
63.并查集,最好k1=fin(x),k2=fin(y),然后合并:fa[k1]=k2
这样不容易错。先要提出来树的根部,把根部进行合并才行。
合并和x,y没有半毛钱关系。
64.快速乘,想卡常的话,必须先对x,y取一个mo
否则x,y太大,ret+x>=mod?ret+x-mod:ret+x 如果mod较小,并不能降到mod以下。
还是会爆long long
(解决方案:用取模卡常的时候,必须警惕能否真正实现取模,
其实不卡常也无所谓,并不能优化太多其实)
65.long long能不开就不开,容易被卡常。
取模1e9+7,可以直接强制转化为long long避免空间过大。
66.注意数据范围~!!!!!
最后的点不一定是最大的。
([SDOI2011]染色,n其实是1e5的,,,最后的是1e4.。。。)
(2018.10.10模拟赛T3,k=0的点,但是n是5e5.。。。。得特判,白丢2分)
67.hash的一个小锅
如果取到0的话,可能与长度不同的情况冲突。
如果映射成:s[i]-'A'
那么,AAB,AB哈希值就是一样的了。多出的A是0*60^2,没有用。
(相当于你hash进制数的进制下出现了前导0!!!)
写成s[i]-'A'+1才行。
68.Tarjan:
if(!dfn[y]) tarjan(y),low[x]=min(low[x],low[y])
别忘了low
69.普通平衡树
①求排名rank的时候,如果t[x].val==c ,ret+=t[t[x].ch[0]].sz别忘了
②哨兵经常容易被干掉。指的是sz不是0了。在根变成空的时候,如果pushup一下,0的sz就变了。
所以,最好的方法是,pushup特判x=0
或者,删掉最后一个点的时候,不要pushup
③如果while循环,那么路径上走过的点sz注意处理。
70.割点
一个点可能多次满足割点的条件。
如果统计次数的话,不能每次都记入一次。
打bool标记,下来再统计。
71.记录环的时候
如果dfs找环,那么走一圈之后,回到初始点,会再次尝试访问环上最后的点。
稍不注意,就可能和之前最后一个点尝试访问初始点的时候冲突。导致重复统计。
解决方法:暴力记录下初始点。
如果尝试访问初始点,那么才记录。
72.后缀数组
①后缀排序:for(reg i=n;i>=1;--i) sa[c[x[y[i]]]--]=y[i],y[i]=0
注意倒序,注意--的位置。
②求height数组:if(rk[i])==1 continue;if(k)--k
73.后缀自动机
①init:别忘了cnt=1,nd=1的初值
②ins的时候,处理nq,处理nq的father ,处理nq的儿子,还要处理nq的出边。然后,还有处理和nq有关的出边(p的祖先们)。一共四条。
③如果要建Parent树边,或者为了topo建图,add中的计数器是tot,别和cnt混用。
④数组大小:点数:O(2*N),Parent树边数:即点数。全图总共的边数:O(3*N)(并不会证)
74.FFT,NTT,FWT
①记得最后除以n
②记得把长度弄到2^n
③最高次项、项数等+1-1和<=,<,的问题处理清楚。我的习惯是,传入项数。然后下标从0开始。f[i]就是i次项系数。
④NTT记得插值是逆元
⑤FWT xor还原时候要除以2
⑥由于要弄长度,所以多项式极其容易空间开小RE。。。。
开成最长多项式长度*2即可。
75.多项式除法,多项式求逆等对(x^m)取模的操作,要么对多项式先取模,要么全算完之后再取模。
千万不可以算完点值就取模,,,插值就不对了。。。
当然,时刻记得取模。
76.如果namespace中的int main不加return 0的话,可能会TLE或者RE等等。所以还是要记得加上。
或者用void main()
77.可持久化trie树,每个节点还有一个根节点,数组别开小。(∑len+N)个节点。
78.计算几何
①精度问题。手写Fabs()处理。eps 1e-7~1e-10
int Fabs(double x){
if(fabs(x)<eps) return 0;
if(x<0) return -1;
return 1;
}
②凸包,stack中至少有三个点。凸包上的点的个数是top,不是n。。。。。
③尽量不用斜率,,特别容易出锅。叉积点积基本就可以办到
④各种特殊情况:
1.斜率为0,斜率不存在
2.判断点在多边形内部时,点可能在多边形边上。
3.半平面交,求直线交点时,直线可能平行,直接除以0.。。。。。
4.半平面交,记得最后先去掉多余线头,再封口(顺序不对的话,就会砍不掉线头的)。p[R]=jiao(q[R],q[L])
79.Tarjan求点双的时候,必须这样写:

判断栈顶为x的话,会出锅。
详见:[SHOI2008]仙人掌图 II——树形dp与环形处理
80.如果要提取一个4位2进制数的每一位
for(reg i=1;i<=4;++i)
num[i]=x&(1<<(i-1))
不能像数位dp一样直接while(tmp),因为高位的0会直接使之break掉。
81.数组不能习惯性开成n。。
N=100000+5
82.一些取模题,仅涉及加加减减的常量,不如先取模为好。否则容易出锅
(HNOI2010 物品调度)
83.各种打标记的时候,如果有标记,别忘了最后清空标记(最好一开始就先写在最后一行)
84.LCT维护信息的时候,link和cut别忘了把信息也更新,然后pushup
询问之前,能pushdown就pushdown!反正一定没错!
85.FFT如果答案是整数的话,那么有可能会有0.00几的精度误差,所以最后还要四舍五入一下
floor(x+0.5)或者round()
86.fhq-treap
1.split的判断条件和当前的now有关
2.记得srand()
87.由于POJ过于XXX
所以注意以下注意事项:
1.不能用bits!
2.不能用%lf!?
3.不能用快读(会TLE)?!?!
4.G++或者C++有的时候会挂,换一个也许就AC了?!?!?!
5.甚至,有的数据自身有锅——!————!——!
忠告:poj做题没有过,二话不说赶紧抄题解代码。否则后果自负。没有题解的题目千万不要做。
88.set找前驱
一定要判:if(it!=s.begin())--it
否则行为未定义!
89.三视图和几何体不唯一对应
例如:
两个都对
90.高斯消元的时候
1.如果当前第i位没有值,continue掉
2.需要swap行向量,别忘了n+1项
91.时刻注意循环范围
1.下标减法不能<0越界
2.不要RE
3.是否符合题意
4.C(n,m)不能存在n<0,m<0,n<m的情况!!否则都会下标<0!!(一个辣鸡题调了一下午)
92.虚树易错点:
1.主要出锅的是“可能不属于关键点的LCA”,记得去重,记得清空,记得和关键点区分开
2.每次虚树之间清空数组
3.虚树外的点的处理(难点)
4.虚树上的边带的边权
5.虚树上的连接实际中可能有一段距离
93.p是质数不一定代表互质!
可能p很小,n,m之类很大,是p的倍数。
求组合数要用LUCAS,不能阶乘逆元
(自古枪兵幸运E)
94.注意覆盖范围
不跨链选择子树的点,
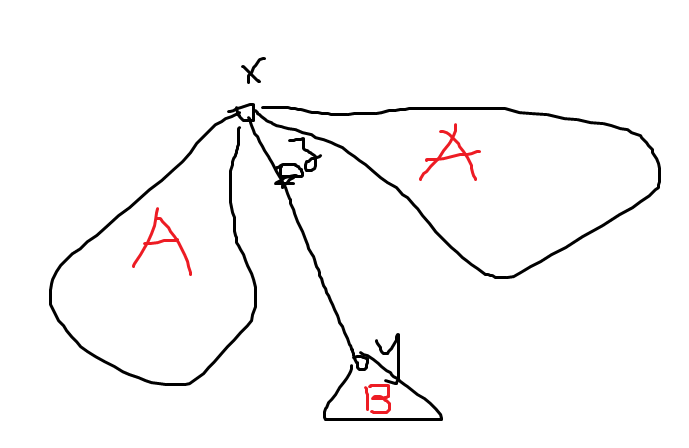
z的子树除了B部分都不能选
95.如果后来改了代码甚至改了思维,一定重新检查!
96.unsigned long long比一般模数的hash冲突概率小
因为模数大啊。。随机情况卡掉概率太低了
但是1e9+7这种单模数随机情况都可能被卡
97.
如果树状数组每个节点维护凸包,如果按照值域下标并且可能取值相同,每个节点凸包元素可能大于lowbit!!!!
如果动态分内存要注意先跑一遍得到maxsize
98.大工程量的题目
1.多测不清空,爆零两行泪
2.多次dfs,多次并查集,多个线段树,尽量变量名起的有区分度(最好都不要起习惯性的名称)
3.注意点数和边数,是否有拆点,慎防RE
99.pushup的锅
1.有的时候只是别的键值的查询,可以不用pushdown
如果没有pushdown,千万不要pushup,儿子的信息不是正确的,直接导致自己的信息也错了
2.别pushup混用了,,,(重组病毒)
3.记得pushup:尤其是fhq的merge和split。。。。
100.UB行为
1.b[++m]=bian(...,...,.m)这个构造函数传入的m是否是++m后的,这是未定义的
2.调用函数f(++m,++m)哪个先++,也是UB的
101.线性筛
记得if(%==0) break
102.KD-Tree
KD-Tree每个节点有实际意义!是平衡树类型!pushup时候要考虑自己!
103.
注意i和mem[i]的区别,尤其是虚树
虚树节点个数可能是2*n的,如果lca直接往里面加的话
104.
假设传入了数组的指针int *a,如果在函数中memset(a,0,sizeof a),
这个sizeof a 其实只是前sizeof int个字节,,也就是a[0]!
必须传入a的长度,进行暴力清空,或者memset(a,0,sizeof len*4)
105.
矩阵快速幂,注意函数内申请单位矩阵ret的时候,预先memset清空!
远古板子害死我了,CF推出式子死活不知所错,,,
106.好东西
https://codeforces.com/problemset/customtest
可以查RE错误,且显示位置。
C++17不支持register
107.
写码农题的时候,一定先理清思路
草稿纸上理清结构,注意事项。
如果大量式子和DP转移分类讨论,和最终代码形式保持一致,方便抄上去
如:6.12考试T1、T3
108.
判断一个二进制数a
1的个数:__builtin_popcount(a)
位数:log2(a)+1
109.线段树
1.每次进入子区间,考虑有没有修改
有修改要pushdown、pushup
没有修改,没有pushdown,就不能pushup
2.注意修改给当前区间带来的影响。
3.注意标记更新的顺序。
110.不要交错程序!
对拍的时候和测大样例的时候,如果修改了记得粘回去!!
mdzz
111.线段树合并
如果还要询问之前的子树,必须新建节点!因为x还承载以前y的信息,pushup就不行了。
否则就跨子树交流了。
112.ST表
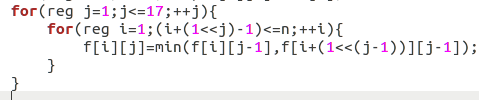
注意(i+(1<<j)-1)<=n!!!
awsl
113.min_25
1.注意区分num(n/i的个数)和cnt(质数个数)
2.注意,int to=(mem[i]/pri[j])<=sqr?id1[mem[i]/pri[j]]:id2[n/(mem[i]/pri[j])]
3.可能ad中传入long long,先对mod取模
