性质+模型转化
首先,一个排列是“好”的,当且仅当:每个数,要么是前缀最大值,要么是后缀最小值。(讨论i和Pi的关系即可证明)
也就是,排列不能存在>=3的下降子序列!
换句话说,假设之前填了i个数,最大值是mx,那么第i+1个数,要么是剩下数的最小值,要么是比mx大的数。
字典序,肯定按位考虑,转化成没有限制的情况,
所以先处理没有限制的情况
这样DP,
$f[i][j]$剩下i个数,比之前最大值大的数有j个的方案数。
第n-i+1个位置,要么填最小值,要么填这j个数之一。
填这j个中第k大的数(它就成为了新的最大值),就只能剩下j-k个比最大值大的了。
转移:$f[i][j]=sum_{k=0}^{j}f[i-1][k]$,k=0代表填了最小值。前缀和优化
当然,i>=j必须保证
然后可以卡位。
之前比最大值大的数有nw个,第i个位置数是ai,
第i个位置:
1.$p_i>a_i$
$p_i$一定是一个比最大值大的数
如果$a_i$是前缀最大值,则nw=n-a[i]
否则,nw=n-前缀最大值
显然为了严格大于,如果nw=0,一定不行。
自由之后,方案数是:$sum_{j=0}^{nw-1}f[n-i][j]=f[n-i+1][nw-1]$
2.$p_i=a_i$
判断$a_i$是不是前缀最大值或者后缀最小值即可
O(T*n^2)
过不去。
瓶颈在于O(n^2)DP
这个DP很模式化啊,,,
$f[i][j]=sum_{k=0}^{j}f[i-1][k]$
能不能发现组合意义?
结论:
$f[i][j]=C(i+j-1,j)-C(i+j-1,j-2)$
证明:
显然必须有i>=j
本质是,(0,0)往(i,j)走,每次要么往右走,要么往右上走,不越过直线(i=j)的方案数。
可以对偶成:从(1,1)走,每次往右往上走,不能越过直线(i=j-1)的方案数
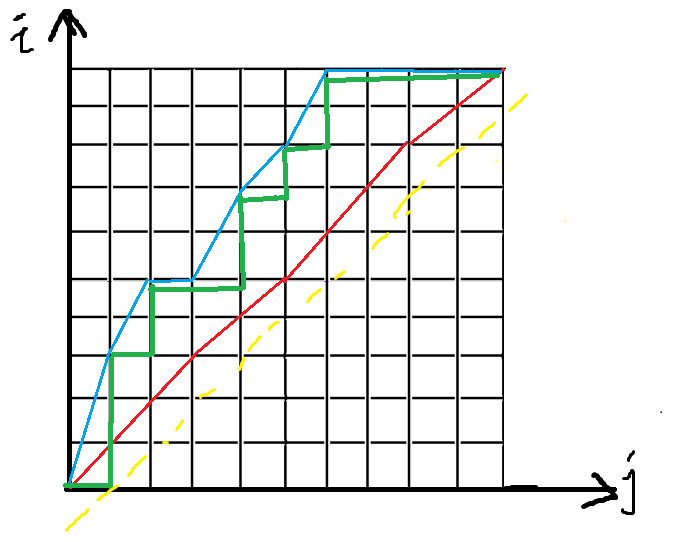
蓝色折线和绿色折线一一对应!
不合法的也一一对应!(请自行画图)
从(1,1)走,每次往右往上走,不能越过直线(i=j-1)的方案数
这个直接卡特兰数一样,对称容斥下即可。
O(n)
// luogu-judger-enable-o2 #include<bits/stdc++.h> #define reg register int #define il inline #define fi first #define se second #define mk(a,b) make_pair(a,b) #define numb (ch^'0') #define pb push_back #define solid const auto & #define enter cout<<endl #define pii pair<int,int> using namespace std; typedef long long ll; template<class T>il void rd(T &x){ char ch;x=0;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb);(fl==true)&&(x=-x);} template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');} template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');} template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar(' ');} namespace Modulo{ const int mod=998244353; il int ad(int x,int y){return x+y>=mod?x+y-mod:x+y;} il int sub(int x,int y){return ad(x,mod-y);} il int mul(int x,int y){return (ll)x*y%mod;} il void inc(int &x,int y){x=ad(x,y);} il void inc2(int &x,int y){x=mul(x,y);} il int qm(int x,int y=mod-2){int ret=1;while(y){if(y&1) ret=mul(x,ret);x=mul(x,x);y>>=1;}return ret;} template<class ...Args>il int ad(const int a,const int b,const Args &...args) {return ad(ad(a,b),args...);} template<class ...Args>il int mul(const int a,const int b,const Args &...args) {return mul(mul(a,b),args...);} } using namespace Modulo; namespace Miracle{ const int N=1200000+5; int n; int jie[N],inv[N]; int C(int n,int m){ if(n<0||m<0||n<m) return 0; return mul(jie[n],inv[m],inv[n-m]); } int F(int n,int m){ if(m==0) return 1; if(m==1) return n; return sub(C(n+m-1,m),C(n+m-1,m-2)); } int a[N]; bool is[N]; int main(){ int t;rd(t); n=N-3; jie[0]=1; for(reg i=1;i<=n;++i) jie[i]=mul(jie[i-1],i); inv[n]=qm(jie[n]); for(reg i=n-1;i>=0;--i) inv[i]=mul(inv[i+1],i+1); while(t--){ rd(n); for(reg i=1;i<=n;++i) rd(a[i]); int mi=n+3; for(reg i=n;i>=1;--i){ is[i]=0; if(a[i]<mi){ mi=a[i]; is[i]=1; } } int ans=0; int nw=n,mx=0; for(reg i=1;i<=n;++i){ nw=n-mx; int lp=nw; if(a[i]>mx) lp=n-a[i]; if(lp){ ans=ad(ans,F(n-i+1,lp-1)); } if(a[i]>mx){ mx=a[i]; }else if(!is[i]){ break; } } printf("%d ",ans); } return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* */
发现本质:一个数要么是前缀最大值,要么是后缀最小值
无限制?可以DP,f[i][j]记录剩下的数以及比最大值大的数
字典序?按位考虑。变成无限制。
O(n^2)?观察DP式子找到组合意义!