[学习笔记]自适应辛普森积分

开计算几何的坑辣

之前就是一些点、线、面、以及凸包、半平面交、旋转卡壳

对于面积的并，如果全是矩形，可以矩形面积并，轮廓线全是直线，可以叉积

当遇到非常不规则的图形组合的时候，如圆弧，就要用到积分了。

好博客：我

辛普森积分

思想：不断用二次函数（最常见简单的带弧函数）拟合图像计算面积。

但是这个拟合，不是直接求出最接近的二次函数，而是用横坐标为l,r,mid三点直接确定二次函数，并且计算积分。

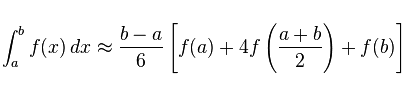
证明见上面博客。

显然直接做，，，精度不知道差到哪里去了。

自适应

思想：不断用二次函数（最常见简单的带弧函数）拟合图像计算面积。通过分治缩小规模以保证精度。

通过和l,lmid,mid加上mid,rmid,r的计算面积进行比较，如果误差在允许范围内，直接返回

否则递归计算左右面积加起来。

显然规模越小，越精确。

复杂度：O(玄学）

适用条件：

其实比较差劲。

图像必须数据范围不大，并且精度要求不高。

而且轮廓线必须“平滑”，出题人不会卡你：

除去三个“角”，如果那个弧线就是抛物线的话，直接凉凉了。

例题

【模板】自适应辛普森法1 套公式。也可以直接手推积分。待定系数法求ln(|ax+b|)的系数

double a,b,c,d,L,R;
double f(double x){
    return (c*x+d)/(a*x+b);
}
double ji(double a,double b){
    return (b-a)/6*(f(a)+f(b)+4*f((a+b)/2));
}
double calc(double l,double r,double eps,double ans){
    double mid=(l+r)/2;
    double le=ji(l,mid),ri=ji(mid,r);
    if(fabs(le+ri-ans)<=eps) return le+ri;
    return calc(l,mid,eps/2,le)+calc(mid,r,eps/2,ri);
}
int main(){
    scanf("%lf %lf %lf %lf %lf %lf",&a,&b,&c,&d,&L,&R);
    printf("%.6lf",calc(L,R,1e-7,ji(L,R)));
    return 0;
}

【模板】自适应辛普森法2 套公式。大力推导（也可以打表），a<0时候不是收敛的。

[NOI2005]月下柠檬树 

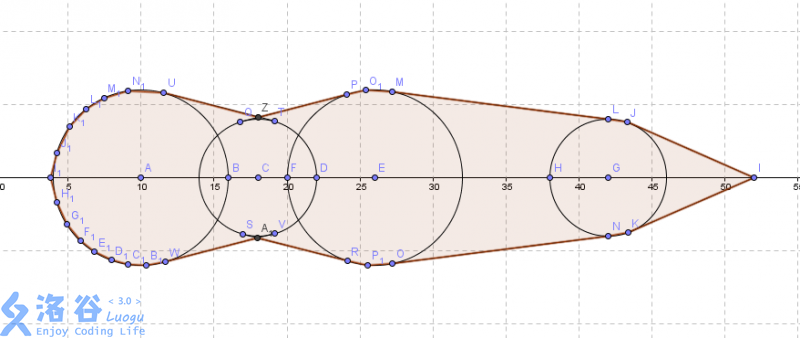
难点在求f(x)

求出相邻圆的公切线（用相似三角形）。求f时候，把所有的圆和线都扫一遍，如果x在其中，则对计算出的纵坐标求max

直接simpson时候传入f(l),f(r),f(mid)可以从6次计算变成2次计算

// luogu-judger-enable-o2
#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=0;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*10+numb);
    (fl==true)&&(x=-x);
}
template<class T>il void output(T x){if(x/10)output(x/10);putchar(x%10+'0');}
template<class T>il void ot(T x){if(x<0) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('
');}

namespace Miracle{
const int N=505;
const double Eps=1e-8;
int n;
struct cir{
    double x,r;
}c[N];
struct po{
    double x,y;
    po(){}
    po(double xx,double yy){
        x=xx;y=yy;
    }
};
struct line{
    po L,R;  
}t[N];
int tot;
double gou(double c,double b){
    return sqrt(c*c-b*b);
}
void com(int i,int j){
    if(c[i].r>c[j].r){
        if(c[i].x+c[i].r+Eps>c[j].x+c[j].r) return;
        ++tot;
        double L=c[j].x-c[i].x;
        double K=L*c[j].r/(c[i].r-c[j].r);
        double S=K>Eps?c[j].r*c[j].r/K:0;
        double P=gou(c[j].r,S);
        t[tot].R=po(c[j].x+S,P);
        K=K+L;
        S=c[i].r*c[i].r/K;
        P=gou(c[i].r,S);
        t[tot].L=po(c[i].x+S,P);
    }else{
        if(c[j].x-c[j].r-Eps<c[i].x-c[i].r) return;
        ++tot;
        double L=c[j].x-c[i].x;
        double K=L*c[i].r/(c[j].r-c[i].r);
        double S=c[i].r*c[i].r/K;
        double P=gou(c[i].r,S);
        t[tot].L=po(c[i].x-S,P);
        K=K+L;
        S=c[j].r*c[j].r/K;
        P=gou(c[j].r,S);
        t[tot].R=po(c[j].x-S,P);
    }
}
double f(double x){
    double ret=0;
    for(reg i=1;i<=n;++i){
        if(c[i].x-c[i].r<=x&&x<=c[i].x+c[i].r){
            double Y=gou(c[i].r,fabs(c[i].x-x));
            if(Y>ret+Eps) ret=Y;
        }
    }
    for(reg i=1;i<=tot;++i){
        if(t[i].L.x<=x&&t[i].R.x>=x){
            double deta=(t[i].R.x-x)*(t[i].R.y-t[i].L.y)/(t[i].R.x-t[i].L.x);
            double Y=t[i].R.y-deta;
            if(Y>ret+Eps) ret=Y;
        }
    }
    return ret;
}
double ji(double l,double r,double fl,double fr,double fm){
    return (r-l)/6*(fl+fr+4*fm);
}
double calc(double l,double r,double eps,double fl,double fr,double fm,double ans){
    double mid=(l+r)/2;
    double flm=f((l+mid)/2),frm=f((mid+r)/2);
    double le=ji(l,mid,fl,fm,flm),ri=ji(mid,r,fm,fr,frm);
    if(fabs(le+ri-ans)<=15*eps) return le+ri+(le+ri-ans)/15;
    return calc(l,mid,eps/2,fl,fm,flm,le)+calc(mid,r,eps/2,fm,fr,frm,ri);
}
int main(){
    rd(n);
    double alp;scanf("%lf",&alp);
    alp=1/tan(alp);
    scanf("%lf",&c[1].x);
    c[1].x*=alp;
    for(reg i=2;i<=n+1;++i){
        scanf("%lf",&c[i].x);
        c[i].x*=alp;
        c[i].x+=c[i-1].x;
    }
    for(reg i=1;i<=n;++i){
        scanf("%lf",&c[i].r);
    }
    ++n;
    c[n].r=0;
    // for(reg i=1;i<=n;++i){
    //     cout<<i<<" : "<<c[i].x<<" "<<c[i].r<<endl;
    // }
    for(reg i=1;i<n;++i){
        com(i,i+1);
    }
    // cout<<" tot "<<tot<<endl;
    // for(reg i=1;i<=tot;++i){
    //     // cout<<" iii "<<i<<endl;
    //     cout<<t[i].L.x<<" "<<t[i].L.y<<endl;
    //     cout<<t[i].R.x<<" "<<t[i].R.y<<endl;
    // }
    double L=23333333,R=-23333333;
    for(reg i=1;i<=n;++i){
        L=min(L,c[i].x-c[i].r);
        R=max(R,c[i].x+c[i].r);
    }
    double fl=f(L),fr=f(R),fm=f((L+R)/2);
    printf("%.2lf",2*calc(L,R,1e-3,fl,fr,fm,ji(L,R,fl,fr,fm)));
    return 0;
}

}
signed main(){
    Miracle::main();
    return 0;
}

/*
   Author: *Miracle*
*/