历经千百爆零
总算苟上了200
多亏题水,痛失AK
T1:随便贪心即可。解封之后,栈里可能连续弹出要注意。
T2:
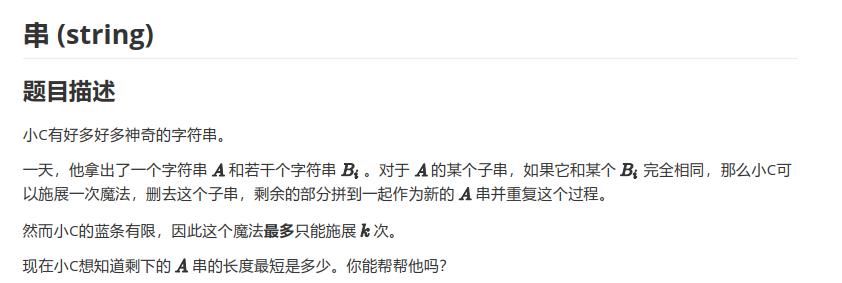

区间dp既视感
直接dp答案不好搞,最优子结构基本没有。。
考虑求cos[l][r]表示删掉l,r花费,
枚举用哪个删
因为一段一段,所以,还要考虑留下的前缀
g[l][r][id][len],[l,r]开始,删到留下第id个串前len位的最小花费
愉快dp
cos完了后,f[i][j]前i位,删了j次留下的最小长度
O(n^3*m*len)必须剪枝
发现,cos[l][r]很大程度上是inf,或者比k大,
所以g的转移的时候,把cos循环到外面,如果cos[s+1][j]大于k-1,直接continue
稳稳AC

#include<bits/stdc++.h> #define reg register int #define il inline #define numb (ch^'0') using namespace std; typedef long long ll; il void rd(int &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=202; const int inf=0x3f3f3f3f; int n,m,k; char a[N]; char b[N][N]; int f[N][N]; int len[N]; namespace sol1{ int nxt[N]; void main(){ int ans=n; for(reg i=1;i<=m;++i){ int l=strlen(b[i]+1); for(reg j=1;j<=n-l+1;++j){ int p=j,t=1; while(t<=l&&b[i][t]==a[p]) ++t,++p; if(t>l) ans=min(ans,n-l); } } printf("%d",ans); } } namespace sol2{ int cos[N][N]; int g[N][N][22][13]; void main(){ memset(cos,inf,sizeof cos); memset(g,inf,sizeof g); for(reg i=1;i<=n;++i){ for(reg j=1;j<=m;++j){ if(len[j]==1&&b[j][1]==a[i]) { cos[i][i]=1; g[i][i][j][len[j]]=0; g[i][i][j][0]=1; } if(b[j][1]==a[i]){ g[i][i][j][1]=0; } } cos[i][i-1]=0; }cos[n+1][n]=0; for(reg i=1;i<=n;++i){ for(reg p=1;p<=m;++p){ g[i][i-1][p][0]=0; } } //cout<<" seee "<<endl; for(reg l=2;l<=n;++l){ for(reg i=1;i<=n;++i){ int j=i+l-1; if(j>n) break; for(reg s=i;s<=j;++s){ cos[i][j]=min(cos[i][j],cos[i][s]+cos[s+1][j]); } for(reg p=1;p<=m;++p)g[i][i-1][p][0]=0; for(reg s=i-1;s<j;++s){ if(s!=i-1&&cos[s+1][j]>k-1) continue; for(reg p=1;p<=m;++p){ // for(reg o=0;o<=len[p];++o){ g[i][j][p][o]=g[i][j][p][o]>g[i][s][p][o]+cos[s+1][j]?g[i][s][p][o]+cos[s+1][j]:g[i][j][p][o]; if(o>=1&&b[p][o]==a[j]) g[i][j][p][o]=min(g[i][j][p][o],g[i][j-1][p][o-1]); } //cos[i][j]=min(cos[i][j],g[i][j][p][len[p]]+1); } } for(reg p=1;p<=m;++p){ cos[i][j]=min(cos[i][j],g[i][j][p][len[p]]+1); } } } // for(reg l=1;l<=n;++l){ // for(reg i=1;i<=n;++i){ // int j=i+l-1; // if(j>n) break; // cout<<" i j "<<i<<" "<<j<<" : "<<cos[i][j]<<endl; // } // } int ans=inf; if(cos[1][n]<=k){ ans=cos[1][n]; printf("%d ",ans);return; } memset(f,inf,sizeof f); f[0][0]=0; for(reg i=1;i<=n;++i){ for(reg j=0;j<=k;++j){ if(j>0){ for(reg p=0;p<i;++p){ if(cos[p+1][i]<=j) f[i][j]=min(f[i][j],f[p][j-cos[p+1][i]]); } } for(reg p=0;p<i;++p){ if(cos[p+1][i-1]<=j) f[i][j]=min(f[i][j],f[p][j-cos[p+1][i-1]]+1); } } } for(reg l=0;l<=k;++l){ ans=min(ans,f[n][l]); } printf("%d ",ans); } } int main(){ rd(n);rd(m);rd(k); scanf("%s",a+1); for(reg i=1;i<=m;++i){ scanf("%s",b[i]+1); len[i]=strlen(b[i]+1); } if(k==1){ sol1::main(); return 0; }else{ sol2::main(); } return 0; } } signed main(){ // freopen("string.in","r",stdin); // freopen("string.out","w",stdout); Miracle::main(); return 0; } /* Author: *Miracle* Date: 2019/1/11 11:26:10 */
本来思路和正解一毛一样
但是以为没有优化空间
g数组每次暴力求的,,其实记录一下用[l,r]就可以少求n次,砍掉1维
然后加上剪枝即可。
以为O(n^3*m*len)过不去,,,
T3:
[SDOI2014]向量集
的弱化版
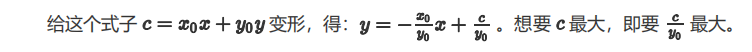
线段树维护凸包即可。
(可能脑残没有推出这个斜率优化的式子,,考虑点积的意义搞的右上凸包,,,当凸包斜率最接近-x/y时最大)

#include<bits/stdc++.h> #define reg register int #define il inline #define mid ((l+r)>>1) #define numb (ch^'0') using namespace std; typedef long long ll; il void rd(int &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=300000+5; int n; struct po{ int x,y; po(){} po(int xx,int yy){ x=xx;y=yy; } bool friend operator <(po a,po b){ if(a.x==b.x) return a.y<b.y; return a.x<b.x; } po friend operator -(po a,po b){ return po(a.x-b.x,a.y-b.y); } }; int cross(po a,po b){ return a.x*b.y-b.x*a.y; } int dot(po a,po b){ return a.x*b.x+a.y*b.y; } bool con(po a,po b){ return (a.x>=b.x)&&(a.y>=b.y); } struct node{ vector<po>mem; }t[4*N]; void upda(int x,po c){ // cout<<" udpa "<<x<<" : "<<c.x<<" "<<c.y<<" "<<t[x].mem.size()<<endl; if(t[x].mem.size()==0) t[x].mem.push_back(c); else if(t[x].mem.size()==1){ if(con(c,t[x].mem[0])) { t[x].mem.pop_back(); } t[x].mem.push_back(c); } else{ while(t[x].mem.size()>1){ int sz=t[x].mem.size(); int tmp=cross(t[x].mem[sz-1]-c,t[x].mem[sz-2]-c); //cout<<" tmp "<<tmp<<endl; if(tmp<=0) t[x].mem.pop_back(); else break; } t[x].mem.push_back(c); } } void pushup(int x){ // cout<<" pushup "<<x<<endl; int ls=x<<1,rs=x<<1|1; int l=0,r=0; int sz=t[ls].mem.size()+t[rs].mem.size(); //cout<<" sz "<<sz<<endl; for(reg i=1;i<=sz;++i){ //cout<<" num i "<<i<<endl; if(l==(int)t[ls].mem.size()){ //cout<<" case 1"<<endl; upda(x,t[rs].mem[r]);++r; }else if(r==(int)t[rs].mem.size()){ //cout<<" case 2"<<endl; upda(x,t[ls].mem[l]);++l; }else if(t[ls].mem[l]<t[rs].mem[r]){ //cout<<" case 3"<<endl; upda(x,t[ls].mem[l]);++l; }else{ //cout<<" case 4"<<endl; upda(x,t[rs].mem[r]);++r; } } //cout<<" szzzzz "<<t[x].mem.size()<<endl; } void ins(int x,int l,int r,int p,po c){ if(l==r){ // cout<<" got "<<l<<" "<<r<<endl; t[x].mem.push_back(c); return; } if(p<=mid) ins(x<<1,l,mid,p,c); else ins(x<<1|1,mid+1,r,p,c); //cout<<" bac to "<<x<<" p "<<p<<" l r "<<l<<" "<<r<<endl; if(p==r) pushup(x); // cout<<" ret "<<endl; } int query(int x,int l,int r,int L,int R,po c){ if(L<=l&&r<=R){ //cout<<" xx "<<x<<" "<<l<<" "<<r<<" "<<t[x].mem.size()<<endl; int ll=0,rr=t[x].mem.size()-1;//warning!!!! -1 int id=0; while(ll<=rr){ int md=(ll+rr)>>1; if(md==0){ id=0;break; }else{ if((t[x].mem[md].y-t[x].mem[md-1].y)*c.y>=(t[x].mem[md-1].x-t[x].mem[md].x)*c.x){ id=md;ll=md+1; }else{ rr=md-1; } } } int ret=0; //cout<<" idid "<<id<<endl; if(id>=0) ret=max(ret,dot(c,t[x].mem[id])); if(id>=1) ret=max(ret,dot(c,t[x].mem[id-1])); if(id<(int)t[x].mem.size()-1) ret=max(ret,dot(c,t[x].mem[id+1])); return ret; } int ret=0; if(L<=mid) ret=max(ret,query(x<<1,l,mid,L,R,c)); if(mid<R) ret=max(ret,query(x<<1|1,mid+1,r,L,R,c)); return ret; } int main(){ rd(n); int op; int las=0; int x,y,l,r; int now=0; for(reg i=1;i<=n;++i){ rd(op); if(op==1){ rd(x);rd(y); x^=las;y^=las; ++now; //cout<<" op1 "<<x<<" "<<y<<endl; //p[++now].x=x;p[now].y=y; ins(1,1,n,now,po(x,y)); // cout<<" ksdjf "<<endl; }else{ rd(x);rd(y);rd(l);rd(r); x^=las;y^=las;l^=las;r^=las; int ans=query(1,1,n,l,r,po(x,y)); las=ans; printf("%d ",ans); } } return 0; } } signed main(){ // freopen("vector.in","r",stdin); // freopen("vector.out","w",stdout); // freopen("data.in","r",stdin); // freopen("my.out","w",stdout); Miracle::main(); return 0; } /* Author: *Miracle* Date: 2019/1/11 9:33:04 */
总结:
很悬
T2还是不够老练,,这种trick,多积累吧 。而且暴力打的不够果断。还是应该想不出来直接打暴力。差点没有时间
T3斜率优化没有推出来?害的考虑半天几何意义开始还错了。
