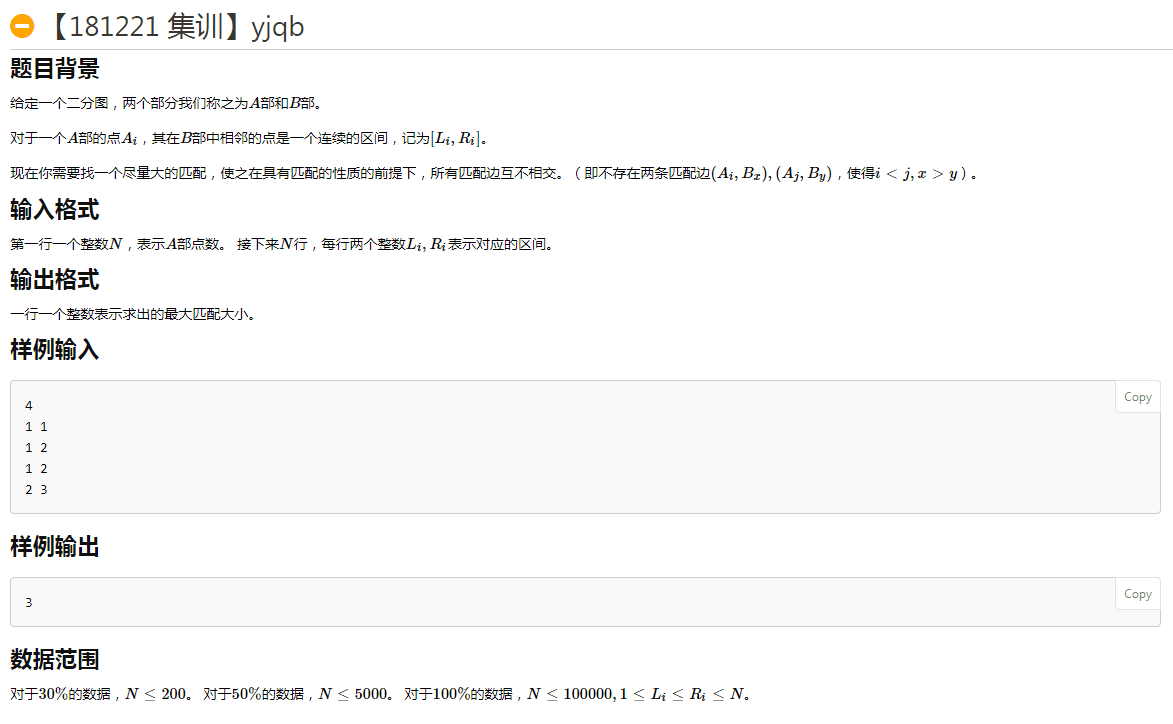
对于这种“不能交叉”的条件,不是很好处理。那么就考虑一下dp
dp[i][j]表示,考虑A中用前i个,考虑连接B中用前j个,最大匹配。(类似LCS的DP)
转移:dp[i][j]=max(dp[i][j-1],dp[i-1][j])当li<=j<=ri时,dp[i][j]=max(dp[i][j],dp[i-1][j-1]+1)
这样可以保证一定不会交叉,而且不会共用匹配点
O(N^2)
看起来非常无法优化。而且我们还没有好好利用区间连边的特点。
观察转移的特点,
一个发现是,这是一个前缀取max,并且某些dp数值的位置+1
由于要和前面的i取max,
那么,把函数键值化,
对于考虑到第i个点,
图像是:
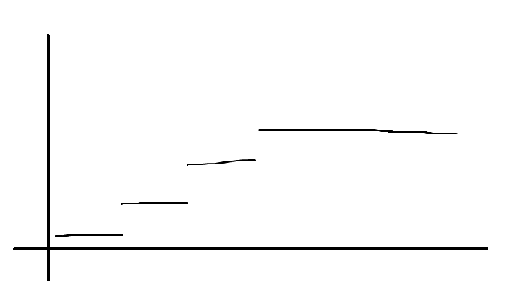
一个分段函数!
考虑如果新加入一个点i的话,在此基础上造成什么影响。
为了方便理解,考虑用滚动数组
dp[j]=max(dp[j],dp[j-1]+1)
这个dp[j]可以直接理解为上一次留下的dp值。(当然转移是倒序循环)
dp[j]=max(dp[j-1],dp[j])这个要正序循环
发现,对于分段函数造成的影响,是一段区间!
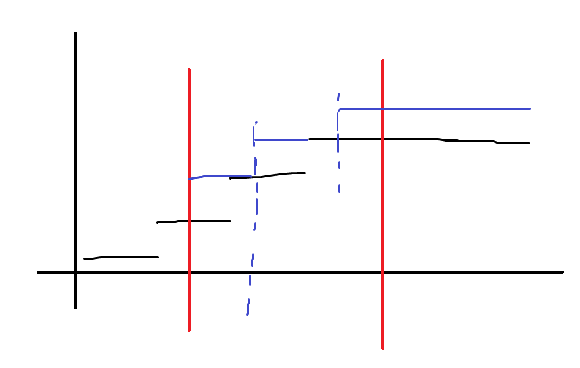
由于dp[j]=max(dp[j],dp[j-1]+1),注意每个分段函数的左端点是不会变化的。
并且,+1的转移都是dp[j]=max(dp[j],dp[j-1]+1)
所以,分段函数的落差都恰好是1!!!
如果可以维护好分段函数,那么最后最高的函数就是ans
怎么维护?
发现这个函数的变化,本质上是把更新区间中涉及到的分段函数向右移动一步,再向上移动一步得到的新的图像!
于是可以打标记了!
这个函数的区间提取,如果用线段树做的话,提取会非常麻烦。而且左移上移怎么处理?!?!
这么灵活的移动,只能交给平衡树了!
ywy_c_asm的大力讨论法:
用三元组[l,r,val]表示每个分段函数的左右端点和高度(函数值)
很多麻烦的事情:
1.边界涉及到函数分离,函数合并。
2.边界可能是某些函数的左端点,
3.和后面的合并?没有后继怎么办?
4.[L,R]只有一个分段函数?要特判
5.[L,R]有两个分段函数?由于不能直接把后面的函数合并到前驱再--r那么简单(其实好像可以?)反正特判比较保险
6.[L,R]有多个分段函数?这时候就要区间打标记了。
7.merge函数那个并入哪一个?
8.split函数,从哪里断开?剩下的l,r是什么?
还有一些splay的基本操作(我写的splay)
1.pre,bac前驱后继,记得pushdown
2.kth,记得pushdown
3.tag的标记打好。
4.左右位置放上空节点方便提取区间。
。。。。。。。。。
还有一堆细节
。。。。。。。。。
放上代码:
大概4+4+4=12种讨论?
删掉注释250行左右

#include<bits/stdc++.h> #define reg register int #define il inline #define ls t[x].ch[0] #define rs t[x].ch[1] #define numb (ch^'0') using namespace std; typedef long long ll; il void rd(int &x){ char ch;x=0;bool fl=false; while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true); for(x=numb;isdigit(ch=getchar());x=x*10+numb); (fl==true)&&(x=-x); } namespace Miracle{ const int N=100000+5; const int nd=3; const int st=1; int n; struct node{ int l,r,v; int fa,ch[2]; int tag; node(){} node(int ll,int rr,int vv){ l=ll,r=rr,v=vv; ch[0]=ch[1]=0; fa=0; tag=0; } void op(){ cout<<" left "<<l<<" right "<<r<<" val "<<v<<endl; cout<<" father "<<fa<<" son1 "<<ch[0]<<" son2 "<<ch[1]<<" tag "<<tag<<endl; } }t[N]; int cnt; int rt; void tag(int x,int c){ t[x].tag+=c; t[x].v+=c; t[x].l+=c; t[x].r+=c; } void pushdown(int x){ if(!t[x].tag) return; // cout<<" pushdown "<<x<<" "<<t[x].tag<<endl; tag(ls,t[x].tag); tag(rs,t[x].tag); t[x].tag=0; } void rotate(int x){ int y=t[x].fa,d=t[y].ch[1]==x; t[t[y].ch[d]=t[x].ch[!d]].fa=y; t[t[x].fa=t[y].fa].ch[t[t[y].fa].ch[1]==y]=x; t[t[x].ch[!d]=y].fa=x; } void splay(int x,int f){ while(t[x].fa!=f){ int y=t[x].fa,z=t[y].fa; if(z!=f){ rotate((t[z].ch[0]==y)&&(t[y].ch[0]==x)?y:x); } rotate(x); } if(f==0) rt=x; } int pre(int x){ splay(x,0); x=t[x].ch[0]; if(!x) return -1; pushdown(x); while(t[x].ch[1]) { x=t[x].ch[1]; pushdown(x); } return x; } int bac(int x){ // cout<<" fin bac "<<x<<" "<<t[x].ch[0]<<endl; splay(x,0); x=t[x].ch[1]; // cout<<" ch[1] "<<x<<" "<<t[x].ch[0]<<endl; if(!x) return -1; pushdown(x); while(t[x].ch[0]) { x=t[x].ch[0]; pushdown(x); } return x; } int kth(int k){ // cout<<" find kth "<<k<<endl; int x=rt; while(x){ pushdown(x); // cout<<" xx "<<x<<endl;t[x].op(); if(t[x].l<=k&&k<=t[x].r) return x; else if(t[x].l>k) x=t[x].ch[0]; else if(t[x].r<k) x=t[x].ch[1]; } return -1;//warning !!! } void merge(int x,int y){ //cout<<" merge "<<x<<" "<<y<<endl; splay(x,0);splay(y,x); t[t[x].ch[1]=t[y].ch[1]].fa=x; t[x].r=t[y].r; } void split(int x,int l,int r){ ++cnt; t[cnt]=node(l,r,t[x].v); t[t[cnt].ch[1]=t[x].ch[1]].fa=cnt; t[cnt].fa=x; t[x].ch[1]=cnt; t[x].r=l-1;//warning!! } void wrk(int L,int R){ // cout<<" wrking ---------------------"<<L<<" "<<R<<endl; int lc=kth(L),rc=kth(R); //cout<<" lc "<<lc<<endl;t[lc].op(); //cout<<" rc "<<rc<<endl;t[rc].op(); if(lc==rc){ // cout<<" Sol 1*****"<<endl; if(L==R){ // cout<<" 1.1%%"<<endl; if(t[lc].l==L){ // int pr=pre(lc); // if(pr==st){ // int bc=bac(lc); // if(bc==nd){ // ++t[lc].v; // }else{ // merge(lc,bc); // // } // } return; } else if(t[lc].r==L){ int bc=bac(lc); if(bc==nd){//las cur split(lc,L,R); ++t[cnt].v; }else{ t[bc].l=L; t[lc].r=L-1; } return; }else{ //cout<<" 1.1.3$$$ "<<endl; int bc=bac(lc); // cout<<" bc "<<bc<<endl; if(bc==nd){ split(lc,L,t[lc].r); ++t[cnt].v; }else{ t[bc].l=L; t[lc].r=L-1; } return; } }else{ if(t[lc].l==L){ int bc=bac(lc); if(bc==nd){//las cur split(lc,t[lc].l+1,t[lc].r); ++t[cnt].v; }else{ t[bc].l=t[lc].l+1; t[lc].r=t[lc].l; } return; }else{ int bc=bac(lc); if(bc==nd){//las cur split(lc,L,t[lc].r); ++t[cnt].v; }else{ t[bc].l=L; t[lc].r=L-1; } return; } } return; } int pr=pre(rc); if(pr==lc){ if(t[lc].l==L&&t[rc].l==R){ t[lc].r=L; t[rc].l=L+1; }else if(t[lc].l==L){ int bc=bac(rc); if(bc==nd){ split(rc,t[rc].l+1,t[rc].r); ++t[cnt].v; }else{ t[bc].l=t[rc].l+1; t[rc].r=t[rc].l; } t[rc].l=L+1; t[lc].r=L; }else if(t[rc].l==R){ t[rc].l=L; t[lc].r=L-1; }else{ int bc=bac(rc); if(bc==nd){ split(rc,t[rc].l+1,t[rc].r); ++t[cnt].v; }else{ t[bc].l=t[rc].l+1; t[rc].r=t[rc].l; } t[rc].l=L; t[lc].r=L-1; } } else{ //cout<<" Sol 3*******"<<endl; if(t[rc].l==R){ merge(pr,rc); rc=pr; t[rc].r--; }else{ // cout<<" 3.1.2$$$"<<endl; int bc=bac(rc); // cout<<" bac "<<bc<<endl; if(bc==nd){ t[rc].r--; }else{ merge(rc,bc); t[rc].r--; } } if(t[lc].l==L){ split(lc,L,t[lc].r); t[lc].r=L; lc=cnt; }else{ split(lc,L-1,t[lc].r); t[lc].r=L-1; lc=cnt; } int LL=pre(lc),RR=bac(rc); splay(LL,0);splay(RR,LL); //cout<<" LL "<<LL<<endl;t[LL].op(); // cout<<" RR "<<RR<<endl;t[RR].op(); tag(t[RR].ch[0],1); } } int calc(){ splay(nd,0); int cur=pre(nd); return t[cur].v; } int main(){ rd(n); rt=1; t[++cnt]=node(-1,-1,0); t[cnt].fa=0; t[cnt].ch[1]=cnt+1;++cnt; t[cnt]=node(0,n,0); t[cnt].fa=1; t[cnt].ch[1]=cnt+1;++cnt; t[cnt]=node(n+1,n+1,0); t[cnt].fa=2; // cout<<t[1].fa<<" "<<t[1].ch[0]<<" "<<t[1].ch[1]<<endl; // cout<<t[2].fa<<" "<<t[2].ch[0]<<" "<<t[2].ch[1]<<endl; // cout<<t[3].fa<<" "<<t[3].ch[0]<<" "<<t[3].ch[1]<<endl; int L,R; for(reg i=1;i<=n;++i){ rd(L);rd(R); wrk(L,R); // cout<<" after wrk "<<cnt<<endl; } printf("%d ",calc()); return 0; } } signed main(){ Miracle::main(); return 0; } /* Author: *Miracle* Date: 2018/12/24 13:54:20 */
太TMD麻烦了。。。。。(要不是为了锻炼码力才不写)
发现之前的方法麻烦的地方在于,维护[l,r]这个区间要来回讨论。函数值+1要讨论。左端点要讨论。split,merge要讨论。。。
落差都是1,怎么利用呢?
用一些点来维护分段函数!
每个点表示这个分段函数的左端点。维护点的横坐标
修改的时候,
[l,r)的左端点集体右移,加入一个l点,把>=r最小的点删除。没了。
原因是,我们不记录高度,一个函数值左边的点的个数,就是函数值的大小!
所以,插入一个点相当于对后面的所有点高度+1,只需要将点向右平移。
同时,代替合并函数值的是,把>=r的点删除掉。
一个关键点在r的位置,并不能+1,所以是开区间。
最后点的个数就是函数值!
总结:
1.DP首先要想到。观察转移,得到分段函数的性质
2.分段函数的移动,可以模式化,所以可以打标记。
3.平衡树维护分段函数,以及一些小技巧。
