排序算法(Sort Algorithm)
给定一个$n$个元素的线性表$(a_0, a_1, dots, a_{n- 1})$,排序算法返回重新排序的结果$(A_0, A-1, dots, A_{n - 1})$,满足$A_0<=A_1<=dots<=A_{n - 1}$。这里的小于等于号可以替换为其他比较的符号。
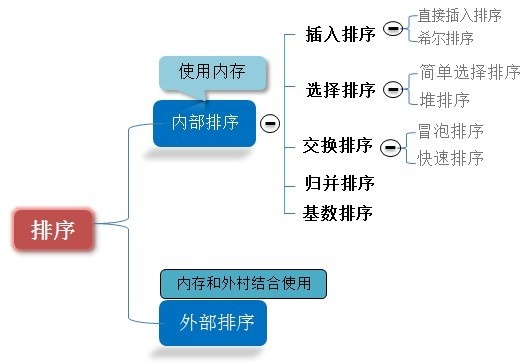
排序的分类
内部排序和外部排序
根据排序过程中元素是否完全保存在内存中,算法分为内部排序(internal sort)和外部排序(external sort)。后者通常因为数据量很大,内存一次不能容纳全部的待排数据,所以将数据放在外存中,在排序过程中需访问外存(即存在数据传输)。
比较排序和非比较排序
比较排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破$O(nlogn)$,因此也称为非线性时间比较类排序。
非比较排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下限,以线性时间运行,因此也称为线性时间非比较类排序。

常见的快速排序、冒泡排序、堆排序、归并排序等都属于比较类排序。在排序的最终结果里,元素之间的次序依赖于它们之间的比较。每个元素都必须和其它元素进行比较才能确定自己的位置。
例如在冒泡排序中,问题规模为$n$,又因为需要比较$n$次,所以平均时间复杂度为$O(n^2)$,在归并排序,快速排序之类的排序中,问题规模通过分治法削减为$log n$,所以时间复杂度平均$O(nlogn)$。
对于现在有的排序算法,我们已经证明其中几种(堆排序、归并排序)的运行时间上界$O(nlogn)$和比较排序算法(不考虑不用通过比较获得结果的希尔排序)的最坏情况的下界是相等的,也就是说,这几种算法已经是渐进最优的排序算法。
比较排序的优势是适用于各种规模的数据,也不在乎数据的分布,都能进行排序。可以说,比较排序适用于一切需要排序的情况。计数排序、基数排序、桶排序则属于非比较排序 。非比较排序是通过确定每个元素之前,应该有多少个元素来排序。即针对数组arr,计算arr[i]之前有多少个元素,则唯一确定了arr[i]在排序后数组中的位置 。非比较排序只要确定每个元素之前的已有的元素个数即可,所有一次遍历即可解决。算法时间复杂度O(n)。非比较排序时间复杂度底,但由于非比较排序需要占用空间来确定唯一位置,所以对数据规模和数据分布有一定的要求。
稳定排序和不稳定排序
对于一个算法,如果任意两个元素$a_i$和$a_j$在排序前的线性表中满足条件$i<j$且$a_i = a_j$,在排序后$a_i$仍在$a_j$之前,则称这个排序算法为稳定排序(Stable Sort),否则称这个算法为不稳定排序(Unstable Sort)。
常见的稳定排序有:插入排序、冒泡排序、归并排序、基数排序
常见的不稳定排序有:选择排序、快速排序、堆排序、希尔排序
时空复杂度
时间复杂度:对排序数据的总的操作次数。反映当$n$变化时,操作次数呈现什么规律。
空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模$n$的函数。
- 平方阶$O(n^q)$排序,各类简单排序:简单插入排序、选择排序和冒泡排序。
- 线性对数阶$O(nlogn)$排序:快速排序、堆排序和归并排序;
- $O(n1 + §))$排序,§ 是介于 0 和 1 之间的常数。 希尔排序
- 线性阶$O(n)$排序:基数排序,此外还有桶排序、箱排序。
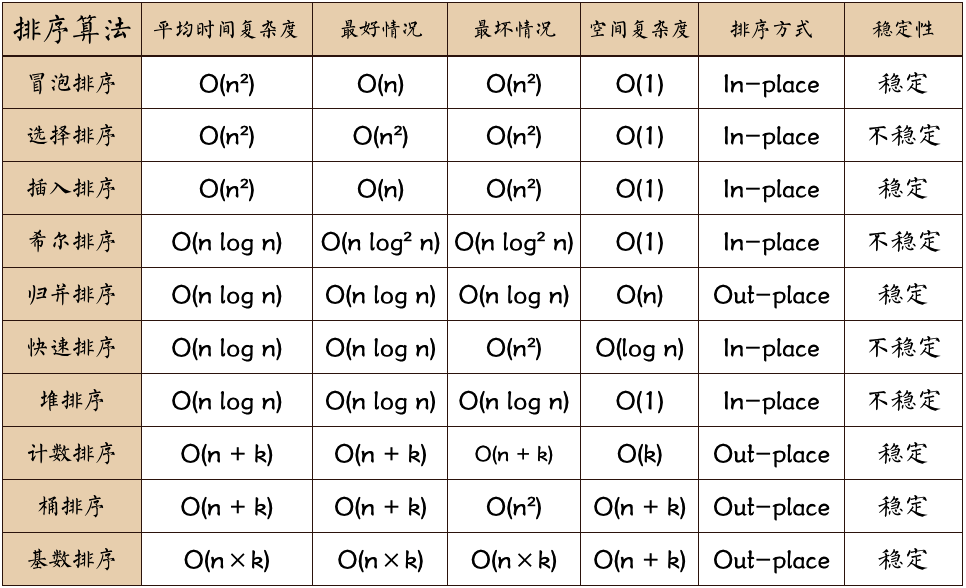
- n: 数据规模
- k: “桶”的个数
- In-place: 占用常数内存,不占用额外内存
- Out-place: 占用额外内存
动画演示
下面使用动画(动画来源网络,见水印)简单展示各个排序算法的实现原理,点击对应动画下的链接可跳转至相应算法详情页。










总结表格

参考资料:
https://blog.csdn.net/coolwriter/article/details/78732728
https://blog.csdn.net/weixin_41190227/article/details/86600821
https://www.cnblogs.com/onepixel/articles/7674659.html
https://www.jianshu.com/p/1af509b2be08