对常见排序算法进行总结,下图可做参考:

在介绍排序算法之前先明确几个概念:
1、时间复杂度:从序列的初始状态到最终排序好的结果状态所花费的时间度量,主要取决于变换、移位等操作语句的执行次数。
2、空间复杂度:从序列的初始状态到最终状态所花费的空间开销,即排序过程中所需要开辟的新的内存空间。
3、稳定性:排序算法是否会改变大小相等元素的相对次序,比如在原序列中r[i]=r[j]、且r[i]在r[j]之前,而排序后r[i]仍在r[j]之前,则该排序算法是稳定的。
4、内部外部排序:内部排序是指不需要开辟新的数组空间,在原先序列的内存中即可完成排序;而外部排序需要借助新的内存空间。
下面依次介绍,并贴上自己的C++实现代码(以从小到大排列为例):
一、冒泡排序
原理:从前往后访问要排序的序列,每次比较相邻两个元素,若相对位置不符合排序要求,则将它们互换。
需要两层循环实现,外层循环表示排序的趟数,n个数据需要n-1趟,外层每次循环结束都会有一个最大的元素“下沉”到序列尾,而小元素则随着比较慢慢“上浮”,这也是冒泡排序名称的来由。
内层循环表示每趟需要排序的元素,m趟排完后就会有m个元素已经有序,不参与m+1趟排序。
时间复杂度:平均为O(n2)、最好情况为O(n) 、最坏情况为O(n2)
空间复杂度:不需要开辟大量新的内存,仅需一个地址用于交换数据,为O(1)
实现代码:
1 //交换元素 2 void Swap(int &a, int &b) 3 { 4 int useValue = 0; 5 useValue = a; 6 a = b; 7 b = useValue; 8 } 9 //冒泡排序 10 void BubbleSort(vector<int> &arr) 11 { 12 for (int i = 0; i < arr.size() - 1; i++) 13 { 14 for (int j = 0; j < arr.size() -1 - i; j++) 15 { 16 if (arr[j] > arr[j + 1]) Swap(arr[j + 1], arr[j]); 17 } 18 } 19 } 20 int main() 21 { 22 vector<int> arr = {5, 5, 6, 12, 1, 12, 23, 19, 20, 24, 19, 19, 19, 19, 15, 15, 3, -2}; 23 BubbleSort(arr); //冒泡排序 24 for (auto ele : arr) cout << ele << " "; 25 cout << endl; 26 return 0; 27 }
二、选择排序
原理:遍历序列找到当前序列中最小元素的位置并记录,将其与序列最前面元素交换,得到一部分有序序列,下次遍历仅遍历后面无序的序列,直到所有元素均有序。这种排序方法避免了冒泡排序中数据交换次数过多的问题。
也需要两层循环实现,每趟排序使最小的元素上浮到本次排序的最前面,下一趟排序时,已经有序的元素不再参与。
时间复杂度:因为不管是否序列已有序,都要比较并记录位置,故平均情况、最好情况、最坏情况均为O(n2)
时间复杂度:O(1)
实现代码:
1 //交换元素 2 void Swap(int &a, int &b) 3 { 4 int useValue = 0; 5 useValue = a; 6 a = b; 7 b = useValue; 8 } 9 //选择排序 10 void SelectSort(vector<int> &arr) 11 { 12 for (int i = 0; i < arr.size(); i++) 13 { 14 int location = i; 15 for (int j = i + 1; j < arr.size(); j++) 16 { 17 if (arr[j] < arr[location]) location = j; 18 } 19 Swap(arr[i], arr[location]); 20 } 21 } 22 int main() 23 { 24 vector<int> arr = {5, 5, 6, 12, 1, 12, 23, 19, 20, 24, 19, 19, 19, 19, 15, 15, 3, -2}; 25 SelectSort(arr); //选择排序 26 for (auto ele : arr) cout << ele << " "; 27 cout << endl; 28 return 0; 29 }
三、插入排序
原理:构建有序序列,对于未排序的无序部分,遍历有序部分并找合适的地方插入,直到所有元素均已有序。
需要两层循环,外层循环表示比较的趟数,排完m趟就会有m个元素已经有序,并放置于序列前面部分,下一趟会遍历这m个元素,并将m+1个元素插入到它们中合适的位置;内层循环表示这一趟已经有序元素的个数。
插入排序可以借助外部内存实现,那样更好理解一点,但是也可以直接内部排序。
时间复杂度:平均为O(n2)、最好情况为O(n) 、最坏情况为O(n2)
空间复杂度:O(1)
实现代码:
1 //插入排序 2 void InsertSort(vector<int> &arr) 3 { 4 for (int i = 0; i < arr.size(); i++) 5 { 6 int j, tmp = arr[i]; 7 for (j = i; j > 0; j--) 8 { 9 if (arr[j - 1] <= tmp) break; 10 else arr[j] = arr[j - 1]; 11 } 12 arr[j] = tmp; 13 } 14 } 15 int main() 16 { 17 vector<int> arr = {5, 5, 6, 12, 1, 12, 23, 19, 20, 24, 19, 19, 19, 19, 15, 15, 3, -2}; 18 InsertSort(arr); //插入排序 19 for (auto ele : arr) cout << ele << " "; 20 cout << endl; 21 return 0; 22 }
四、希尔排序
原理:加强版的插入排序,先将整个待排序的序列分割成为若干子序列,分别进行直接插入排序,待整个序列中的记录"基本有序"时,再对全体记录进行依次直接插入排序。避免了插入排序每次只能将数据移动一位的缺陷。
需要设定一个希尔序列增量t,如果序列长度为n,可以设置t的初始值为n/2,但t是递减的,需要设定递减规则但最终t必须要递减到1,可以设置规则为t=t/2。对每一个t值,都会有若干组数据在进行插入排序,当t=1时,整个序列已经基本有序,再排一趟就可以完成整体排序。
举个例子:对12,3,16,8,9,14,1,36,9,11这十个数排序
当t=n/2=5时,对12,14;3,1;16,36;8,9;9,11这五组序列插入排序(增量为5),得到12,1,16,8,9,14,3,36,9,11;
当t=t/2=2时,对12,16,9,3,9和1,8,14,36,11这两组序列插入排序(增量为2),得到3,1,9,8,9,11,12,14,16,36;
当t=t/2=1时,直接对上一步得到的序列插入排序(增量为1),得到1,3,8,9,9,11,12,14,16,36。
时间复杂度:希尔排序的时间复杂度计算很复杂,平均可认为是O(nlogn)即可,最好情况为O(n) 、最坏情况为O(n2)。最上面的表格中可能有错误。
空间复杂度:O(1)
实现代码:
1 //希尔排序 2 void ShellSort(vector<int> &arr) 3 { 4 int shellValue = arr.size() / 2; //定义希尔值 5 while (shellValue >= 1) 6 { 7 for (int i = shellValue; i < arr.size(); i++) 8 { 9 int j, tmp = arr[i]; 10 for (j = i; j / shellValue > 0; j = j - shellValue) 11 { 12 if (tmp >= arr[j - shellValue]) break; 13 else arr[j] = arr[j - shellValue]; 14 } 15 arr[j] = tmp; 16 } 17 shellValue = shellValue / 2; 18 } 19 } 20 int main() 21 { 22 vector<int> arr = {5, 5, 6, 12, 1, 12, 23, 19, 20, 24, 19, 19, 19, 19, 15, 15, 3, -2}; 23 ShellSort(arr); //希尔排序 24 for (auto ele : arr) cout << ele << " "; 25 cout << endl; 26 return 0; 27 }
五、归并排序
原理:采用分治法的原理,建立在归并操作的基础上。一般是自上而下的递归,将初始序列分为两半,两半再分为四份,四份分为八份.......直到每一份仅含一个元素,然后两个相邻的元素比较,按大小排序得到一组,一组再与相邻的组归并得到更大的组,更大的组再与其他组归并,直到所有元素均已有序。
举个例子表示归并的方式:归并2,8,14,20,21和1,9,15两组序列,需要先开辟新的内存空间,然后按大小顺序将元素放入,先放1,再放2,8,接着是14..........直到得到1,2,8,9,14,15,20,21完成归并操作。
归并排序需要开辟新的内存,所以是一种外部排序。
时间复杂度:递归过程可看作利用了二叉树结构,共需要nlogn次完成分割,每次比较N次,故平均情况、最好情况、最坏情况均为O(nlogn)
空间复杂度:O(n)
实现代码:
1 //归并排序 2 vector<int> MergeSort(vector<int> &arr) 3 { 4 if (arr.size() < 2) return arr; 5 else 6 { 7 int middle = arr.size() / 2; 8 return Merge(MergeSort(vector<int>(arr.begin(), arr.begin() + middle)), MergeSort(vector<int>(arr.begin() + middle, arr.end()))); 9 } 10 } 11 //归并排序中具体归并过程 12 vector<int> Merge(vector<int> left, vector<int> right) 13 { 14 vector<int> result; 15 vector<int>::iterator leftVec = left.begin(), rightVec = right.begin(); 16 while (leftVec != left.end() && rightVec != right.end()) 17 { 18 result.push_back((*leftVec <= *rightVec) ? (*leftVec++) : (*rightVec++)); 19 } 20 while (leftVec != left.end()) result.push_back(*leftVec++); 21 while (rightVec != right.end()) result.push_back(*rightVec++); 22 return result; 23 } 24 int main() 25 { 26 vector<int> arr = {5, 5, 6, 12, 1, 12, 23, 19, 20, 24, 19, 19, 19, 19, 15, 15, 3, -2}; 27 vector<int> result = MergeSort(arr); //归并排序 28 for (auto ele : result) cout << ele << " "; 29 cout << endl; 30 return 0; 31 }
六、快速排序
原理:在元素中挑出一个“基准”元素,拿其他元素与之比较,将基准放在中间,比基准小的都放在左边,大的都放在右边,然后递归对基准左、右边序列再进行这样的排序,直到所有元素有序。
快速排序也是“分治法”的一种实现,它是平均情况下最快、效率最高的排序算法,虽然最坏状况下需要 Ο(n2) 次比较,但这种状况并不常见。快排通常明显比其他 Ο(nlogn) 算法更快,因为它的内部循环可以在大部分的架构上很有效率地被实现出来,而且O(nlogn) 记号中隐含的常数因子很小,比复杂度稳定等于 O(nlogn) 的归并排序要小很多。
时间复杂度:平均为O(nlogn)、最好情况为O(nlogn) 、最坏情况为O(n2)
空间复杂度:需要记录递归过程,故空间复杂度为递归深度O(logn)
实现代码:(通常情况下由多个函数辅助实现,但也可以由一个函数单个实现)
1 //交换元素 2 void Swap(int &a, int &b) 3 { 4 int useValue = 0; 5 useValue = a; 6 a = b; 7 b = useValue; 8 } 9 //快速排序 10 void QuickSort(vector<int> &arr, int left, int right) 11 { 12 if (right - left >= 0) 13 { 14 int midValue = arr[left - 1]; 15 int midLocation = left - 1; 16 int rightLocation = right; 17 18 while (left != right) 19 { 20 while (arr[left] <= midValue && left < right) left++; 21 while (arr[right] >= midValue && left != right) right--; 22 Swap(arr[left], arr[right]); 23 } 24 if (arr[left] >= midValue) left--; right--; 25 if (arr[left] < midValue) Swap(arr[midLocation], arr[left]); 26 QuickSort(arr, midLocation + 1, left - 1); 27 QuickSort(arr, left + 2, rightLocation); 28 } 29 } 30 int main() 31 { 32 vector<int> arr = {5, 5, 6, 12, 1, 12, 23, 19, 20, 24, 19, 19, 19, 19, 15, 15, 3, -2}; 33 QuickSort(arr, 1, arr.size() - 1); //快速排序 34 for (auto ele : arr) cout << ele << " "; 35 cout << endl; 36 return 0; 37 }
七、堆排序
原理:要想介绍堆排序的原理,就需要先介绍什么是堆及堆的常见操作。
在数据结构中有一种树结构称为完全二叉树:若设二叉树的深度为n,则除第n层外其他各层的节点数都达到最大个数,且第n层上的所有节点都集中在最左侧。
堆就是完全二叉树,且一般情况下堆分为最大堆和最小堆,最大堆中每个父节点元素都大于或等于两个子节点,最小堆则相反。所以最大堆中根节点就是整个序列中的最大值,最小堆中是最小值。
比如下图就是一个最小堆:
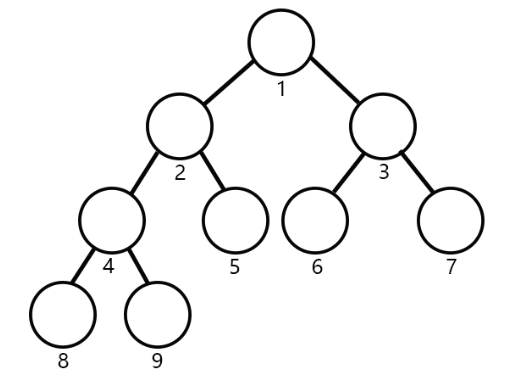
堆可以用数组结构来存储,按从上到下、从左到右的顺序,对应于数组的下标编号。节点i的左子节点为2i+1,右子节点为2i+2,父节点为(i-1)/2。
对于堆,常见的操作有上浮、下沉、插入、弹出、取顶和堆排序,本文仅介绍堆排序,想了解堆其他操作的可以看这篇:https://www.cnblogs.com/schips/p/10660163.html
堆排序的思路其实很简单,如果想从小到大排序,则构建最大堆,首先对全部n个元素构建最大堆,此时根节点为最大值,将根节点取出与最后一个节点交换,然后最后的节点不再参与运算,对剩下的n-1个元素构建堆,依次操作,直到所有元素有序。
堆排序中关键点在于构建堆的过程,可以理解为从最后一个父节点开始,依次往上对每个节点进行下沉。
时间复杂度:平均情况、最好情况、最坏情况均为O(nlogn)
空间复杂度:O(1)
实现代码:(构建堆过程中下沉操作可以用while循环实现,这里我使用了递归方式)
1 //交换元素 2 void Swap(int &a, int &b) 3 { 4 int useValue = 0; 5 useValue = a; 6 a = b; 7 b = useValue; 8 } 9 //堆排序 10 void HeapSort(vector<int> &arr) 11 { 12 int sizeBegin = arr.size(); 13 for (int i = 0; i < sizeBegin; i++) 14 { 15 BuildHeap(arr, sizeBegin - i); //构建最大堆 16 Swap(arr[0], arr[sizeBegin - 1 - i]); 17 } 18 } 19 //构建最大堆 20 //参数为序列的引用和序列长度 21 void BuildHeap(vector<int> &arr, int size) 22 { 23 if (size > 1) //仅当序列中有至少两个元素时才构建堆 24 { 25 for (int i = size / 2 - 1; i >= 0; i--) AdjustHeap(arr, size, i); 26 } 27 } 28 //调整堆 29 //参数为序列的引用、序列长度和要调整节点的位置 30 void AdjustHeap(vector<int> &arr, int size, int location) 31 { 32 int leftChild = location * 2 + 1; //左子节点 33 int rightChild = location * 2 + 2; //右子节点 34 if (rightChild < size) //表示该节点既有左子节点,也有右子节点 35 { 36 int maxChild = arr[leftChild] > arr[rightChild] ? arr[leftChild] : arr[rightChild]; 37 if (arr[location] < maxChild) 38 { 39 if (maxChild == arr[leftChild]) 40 { 41 Swap(arr[location], arr[leftChild]); 42 AdjustHeap(arr, size, leftChild); 43 } 44 else 45 { 46 Swap(arr[location], arr[rightChild]); 47 AdjustHeap(arr, size, rightChild); 48 } 49 } 50 } 51 else if (leftChild < size) //只有左子节点 52 { 53 if (arr[location] < arr[leftChild]) Swap(arr[location], arr[leftChild]); 54 } 55 } 56 int main() 57 { 58 vector<int> arr = {5, 5, 6, 12, 1, 12, 23, 19, 20, 24, 19, 19, 19, 19, 15, 15, 3, -2}; 59 HeapSort(arr); //堆排序 60 for (auto ele : arr) cout << ele << " "; 61 cout << endl; 62 return 0; 63 }
八、交换排序
原理:类似于选择排序和冒泡排序,由两层循环完成,外部循环表示排序的趟数,每排一趟找出最小值放到最前面,依次进行直到所有元素有序。
以前经常将这种方法与冒泡排序混淆,其实两者还是有区别的,冒泡排序是相邻的两个数比较并交换数据,而交换排序是用最前面的元素与所有元素比较,如果顺序不符合要求就交换。
与选择排序也很类似,而选择排序省略了数据交换的过程,交换排序需要很多数据交换操作。
时间复杂度:平均为O(n2)、最好情况为O(n) 、最坏情况为O(n2)
空间复杂度:O(1)
实现代码:
1 //交换元素 2 void Swap(int &a, int &b) 3 { 4 int useValue = 0; 5 useValue = a; 6 a = b; 7 b = useValue; 8 } 9 //交换排序 10 void ExchangeSort(vector<int> &arr) 11 { 12 for (int i = 0; i < arr.size() - 1; i++) 13 { 14 for (int j = i + 1; j < arr.size(); j++) 15 { 16 if (arr[i] > arr[j]) Swap(arr[i], arr[j]); 17 } 18 } 19 } 20 int main() 21 { 22 vector<int> arr = {5, 5, 6, 12, 1, 12, 23, 19, 20, 24, 19, 19, 19, 19, 15, 15, 3, -2}; 23 ExchangeSort(arr); //交换排序 24 for (auto ele : arr) cout << ele << " "; 25 cout << endl; 26 return 0; 27 }
除了以上几种排序,常见的还有计数排序、桶排序与基数排序,但应用场景可能比较局限,就不做介绍。感兴趣的可以参考这个链接:https://www.runoob.com/w3cnote/ten-sorting-algorithm.html
本文参考的博文除了以上两个外,还有以下链接,表示感谢: